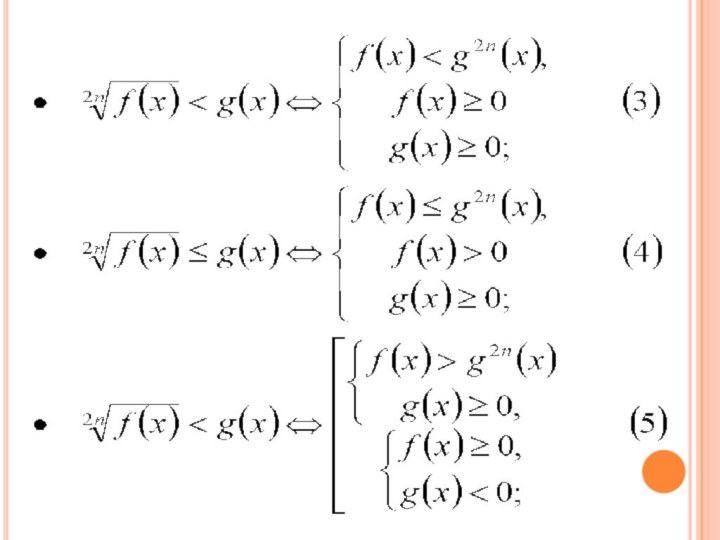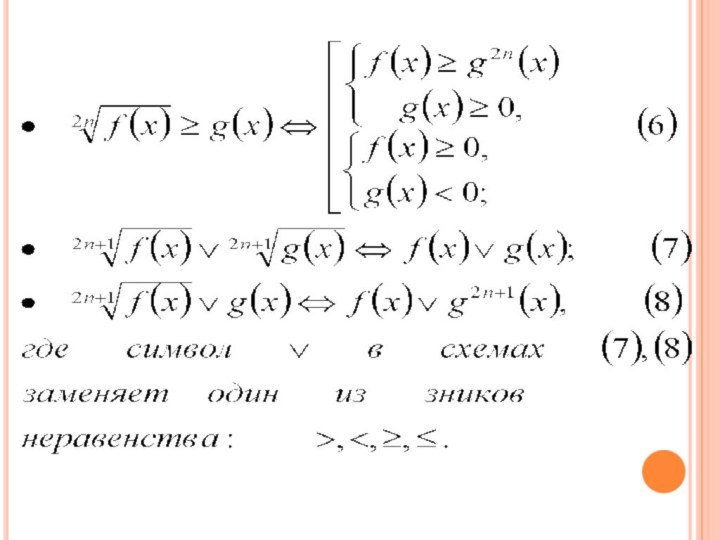Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре Решение неравенств с одной переменной(11 класс)

Содержание

Решение неравенств с одной переменной
Цели: развитие логического мышления формируя умения и навыки решения систем и совокупностей Решение неравенств с одной переменной Определение Таким образом, два неравенства являются равносильными на множестве Х, если множества решений Поэтому вместо того чтобы решать данное неравенство, можно решать любое другое, равносильное Важно понимать, что для доказательства неравносильности двух неравенств нет необходимости решать каждое Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности Системы и совокупности неравенств Определение. Несколько неравенств с одной переменной образуют систему неравенств, если Решить систему неравенств – значит найти все её частные решения. Решение системы Например:Решим систему неравенств:Ответ: Определение. Несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти Решение совокупности неравенств представляет собой объединение решений неравенств, образующих совокупность. Неравенства, образующие совокупность, объединяются квадратной скобкой. НапримерРешим совокупность неравенствОтвет: Задание группам № 57.4а; № 57.5а; № 57.8а. Необходимо вспомнить правила перехода от логарифмического неравенства к системе:№ 57.11 Необходимо рассмотреть два случая: Метод введения новой переменной при решении неравенств57.16 – 57.20 б, 57.21а, 57.22а Домашнее задание№№ 57.4б, 57.5б, 57.857.1056.16-57.20 а Литература:1. А.Г.Мордкович «Алгебра и начала анализа», часть 1, «Мемозина», Москва, 2012.2. А.Г.Мордкович Неравенства, содержащие иррациональные выраженияПриведем некоторые стандартные схемы для решения иррациональных неравенств, в Пример 3. Решите неравенствоРешение. Если 2 - x < 0 или 2 Составим систему неравенств: Составим совокупность систем неравенств: Функционально-графический метод при решении неравенств№ 57.23 – 57.25 а, б Неравенства с модулямиСуществует три способа решения неравенств с модулямиГеометрическийВозведение в квадратУниверсальный (по определению) 1 способ: ГеометрическийПРЕОБРАЗУЕМ НЕРАВЕСТВО: Модуль – это расстояние!!!! 2 способ: возведение в квадратПри условии, если обе части неравенства неотрицательны!!! 3 способ: по определению модуля - универсальныйПо определению, под знаком модуля может
Слайды презентации

Слайд 2 Решение неравенств с одной переменной

Решение неравенств с одной переменной

Слайд 3 Определение
Таким образом, два неравенства являются равносильными на множестве

Определение Таким образом, два неравенства являются равносильными на множестве Х, если множества

Х, если множества решений этих неравенств совпадают.
Два неравенства f₁(х)>g₁(х)

и f₂(х) а) каждое решение первого неравенства, принадлежащее множеству Х, является решением второго, и наоборот, каждое решение второго неравенства, принадлежащее множеству Х, является решением первого;
б) или оба неравенства не имеют решений.

Слайд 4 Поэтому вместо того чтобы решать данное неравенство, можно

Поэтому вместо того чтобы решать данное неравенство, можно решать любое другое,

решать любое другое, равносильное данному.

Замену одного неравенства другим, равносильным

данному на Х, называют равносильным переходом на Х.
Равносильный переход обозначат двойной стрелкой
Например: х²<1 |х|<1.

Слайд 5 Важно понимать, что для доказательства неравносильности двух неравенств

Важно понимать, что для доказательства неравносильности двух неравенств нет необходимости решать

нет необходимости решать каждое из неравенств, а затем убеждаться

в том, что множества их решений не совпадают – достаточно указать одно решение одного из неравенств, которое не является решением другого неравенства.

Слайд 6 Пусть функции f(x), g(x), h(x) определены на множестве

Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности

Х. Шесть теорем о равносильности

Слайд 7 Пусть функции f(x), g(x), h(x) определены на множестве

Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности

Х. Шесть теорем о равносильности

Слайд 8 Пусть функции f(x), g(x), h(x) определены на множестве

Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности

Х. Шесть теорем о равносильности

Слайд 9 Пусть функции f(x), g(x), h(x) определены на множестве

Пусть функции f(x), g(x), h(x) определены на множестве Х. Шесть теорем о равносильности

Х. Шесть теорем о равносильности

Слайд 10 Системы и совокупности неравенств
Определение.
Несколько неравенств с одной переменной

Системы и совокупности неравенств Определение. Несколько неравенств с одной переменной образуют систему неравенств,

образуют систему неравенств, если ставится задача найти все такие

значения переменной, каждое из которых является частным решением заданных неравенств.
Частное решение системы неравенств – значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство.
Множество всех частных решений системы неравенств представляют собой общее решение системы неравенств.

Слайд 11 Решить систему неравенств – значит найти все её

Решить систему неравенств – значит найти все её частные решения. Решение

частные решения.
Решение системы неравенств представляет собой пересечение решений

неравенств, образующих систему.
Неравенства, образующие систему, объединяются фигурной скобкой.

Слайд 12 Например:
Решим систему неравенств:








Ответ:

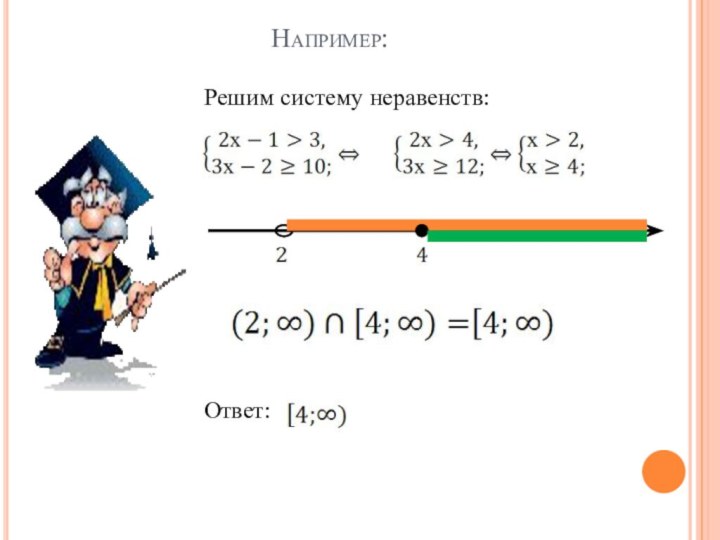
Например:Решим систему неравенств:Ответ:

Слайд 13 Определение.
Несколько неравенств с одной переменной образуют совокупность неравенств,

Определение. Несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача

если ставится задача найти все такие значения переменной, каждое

из которых является хотя бы одного из заданных неравенств.
Каждое такое значение переменной называют частным решением совокупности неравенств.
Множество всех частных решений совокупности неравенств представляет собой решение совокупности неравенств.

Слайд 14
Решение совокупности неравенств представляет собой объединение решений неравенств,

Решение совокупности неравенств представляет собой объединение решений неравенств, образующих совокупность. Неравенства, образующие совокупность, объединяются квадратной скобкой.

образующих совокупность.

Неравенства, образующие совокупность, объединяются квадратной скобкой.

Слайд 15 Например
Решим совокупность неравенств








Ответ:

НапримерРешим совокупность неравенствОтвет:

Слайд 16 Задание группам















№ 57.4а;
№ 57.5а;
№

Задание группам № 57.4а; № 57.5а; № 57.8а.

57.8а.

Слайд 17 Необходимо вспомнить правила перехода от логарифмического неравенства к

Необходимо вспомнить правила перехода от логарифмического неравенства к системе:№ 57.11

системе:
№ 57.11

Слайд 18 Необходимо рассмотреть два случая:

Необходимо рассмотреть два случая:

Слайд 19 Метод
введения новой переменной при решении неравенств
57.16 –

Метод введения новой переменной при решении неравенств57.16 – 57.20 б, 57.21а, 57.22а

57.20 б, 57.21а, 57.22а

Слайд 20 Домашнее задание
№№
57.4б,
57.5б,
57.8
57.10
56.16-57.20 а

Домашнее задание№№ 57.4б, 57.5б, 57.857.1056.16-57.20 а

Слайд 21 Литература:
1. А.Г.Мордкович «Алгебра и начала анализа», часть 1,

Литература:1. А.Г.Мордкович «Алгебра и начала анализа», часть 1, «Мемозина», Москва, 2012.2.

«Мемозина», Москва, 2012.
2. А.Г.Мордкович «Алгебра и начала анализа», часть

2, «Мемозина», Москва, 2012.

Слайд 22 Неравенства, содержащие иррациональные выражения
Приведем некоторые стандартные схемы для

Неравенства, содержащие иррациональные выраженияПриведем некоторые стандартные схемы для решения иррациональных неравенств,

решения иррациональных неравенств, в которых используют возведение в натуральную

степень обеих частей неравенства.

Слайд 23

Слайд 24

Слайд 25 Пример 3. Решите неравенство
Решение. Если 2 - x

Пример 3. Решите неравенствоРешение. Если 2 - x < 0 или

< 0 или 2 - x = 0 ,

то исходное неравенство не выполняется, так как по определению арифметического квадратного корня

Пусть 2 - x > 0 , тогда при возведении обеих частей неравенства в квадрат получим на ее области определения и при условии 2 - x > 0 равносильное неравенство.

Слайд 26 Составим систему неравенств:

Составим систему неравенств:

Слайд 27 Составим совокупность систем неравенств:

Составим совокупность систем неравенств:

Слайд 28 Функционально-графический метод
при решении неравенств
№ 57.23 – 57.25

Функционально-графический метод при решении неравенств№ 57.23 – 57.25 а, б

а, б

Слайд 29 Неравенства с модулями

Существует три способа решения неравенств с

Неравенства с модулямиСуществует три способа решения неравенств с модулямиГеометрическийВозведение в квадратУниверсальный (по определению)

модулями

Геометрический
Возведение в квадрат
Универсальный (по определению)

Слайд 30 1 способ: Геометрический
ПРЕОБРАЗУЕМ НЕРАВЕСТВО:
Модуль – это расстояние!!!!

1 способ: ГеометрическийПРЕОБРАЗУЕМ НЕРАВЕСТВО: Модуль – это расстояние!!!!

Слайд 31 2 способ: возведение в квадрат
При условии, если обе

2 способ: возведение в квадратПри условии, если обе части неравенства неотрицательны!!!

части неравенства неотрицательны!!!

  • Имя файла: prezentatsiya-po-algebre-reshenie-neravenstv-s-odnoy-peremennoy11-klass.pptx
  • Количество просмотров: 189
  • Количество скачиваний: 6
- Предыдущая Разложение на множители (7класс)
Следующая - Тьюторство

Похожие презентации

Открытый урок по теме Линейная функция Открытый урок по теме Линейная функция 181
Степенная функция (11 класс) Степенная функция (11 класс) 174
Тригонометрические уравнения и отбор корней в нем Тригонометрические уравнения и отбор корней в нем 148
Теорема синусов Теорема синусов 155
Презентация о выдающемся математике Колмогорове Презентация о выдающемся математике Колмогорове 190
Элементы комбинаторики, статистики и теории вероятностей. Задания из Открытого банка заданий ЕГЭ, профильный уровень, страница 10 Элементы комбинаторики, статистики и теории вероятностей. Задания из Открытого банка заданий ЕГЭ, профильный уровень, страница 10 180
Тренажёр Решу ВПР: простейшие логические задачи, часть 5 Тренажёр Решу ВПР: простейшие логические задачи, часть 5 206
Презентация по математике на тему Тригонометрические функции Презентация по математике на тему Тригонометрические функции 174
Презентация по геометрии к зачёту по теме Перпендикулярность прямой и плоскости Презентация по геометрии к зачёту по теме Перпендикулярность прямой и плоскости 154
Открытый урок в 8 классе по теме Решение неполных квадратных уравнений Открытый урок в 8 классе по теме Решение неполных квадратных уравнений 160
Шаблоны для презентаций ВПР: математика - 7 Шаблоны для презентаций ВПР: математика - 7 156
Презентация Уравнение касательной к графику функции, 10 класс Презентация Уравнение касательной к графику функции, 10 класс 264
Определить, чётная или нечётная функция Определить, чётная или нечётная функция 164
СТАРИННЫЕ ЗАДАЧИ НА ДРОБИ СТАРИННЫЕ ЗАДАЧИ НА ДРОБИ 173
Презентация по теме Показательная функции Презентация по теме Показательная функции 175
Презентация урока алгебры в 8 классе на тему Десять способов решений квадратных уравнений Презентация урока алгебры в 8 классе на тему Десять способов решений квадратных уравнений 166
Уравнения третьей степени Уравнения третьей степени 147
Графики функций 9 класс Графики функций 9 класс 135
Всё о неравенствах Всё о неравенствах 160
Простые числа Простые числа 474
Решение уравнений с квадратным корнем Решение уравнений с квадратным корнем 179
Презентация по теме Решение квадратных уравнений разными способами Презентация по теме Решение квадратных уравнений разными способами 153
Презентация: Прогрессии. Формулы, 9 класс Презентация: Прогрессии. Формулы, 9 класс 173
Презентация к уроку математики в 7 классе Математическая викторина Презентация к уроку математики в 7 классе Математическая викторина 185
Презентация по алгебре. Свойства функций Презентация по алгебре. Свойства функций 153
Уравнения Уравнения 141
Умножение многочлена на многочлен Умножение многочлена на многочлен 148
Интерполяция и аппроксимация Интерполяция и аппроксимация 190
Умножение многочлена на многочлен 7 класс Умножение многочлена на многочлен 7 класс 179
Алгебра логики на практике Алгебра логики на практике 156