Презентация на тему по математике на тему Построение графиков функций при помощи геометрических преобразований

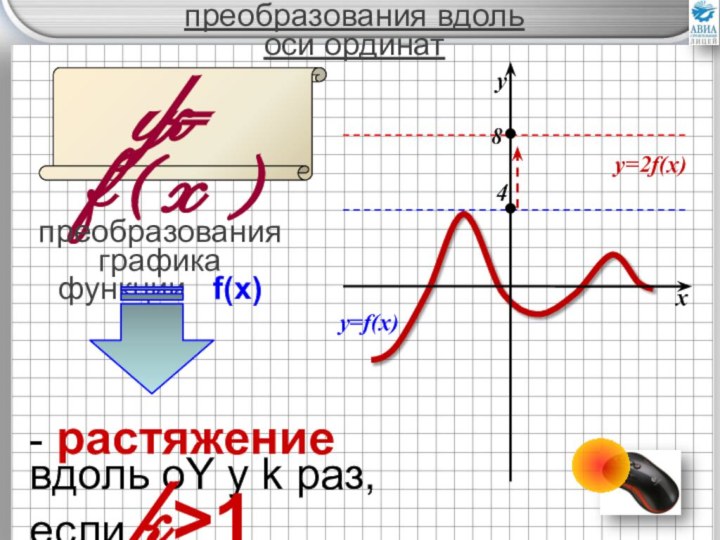
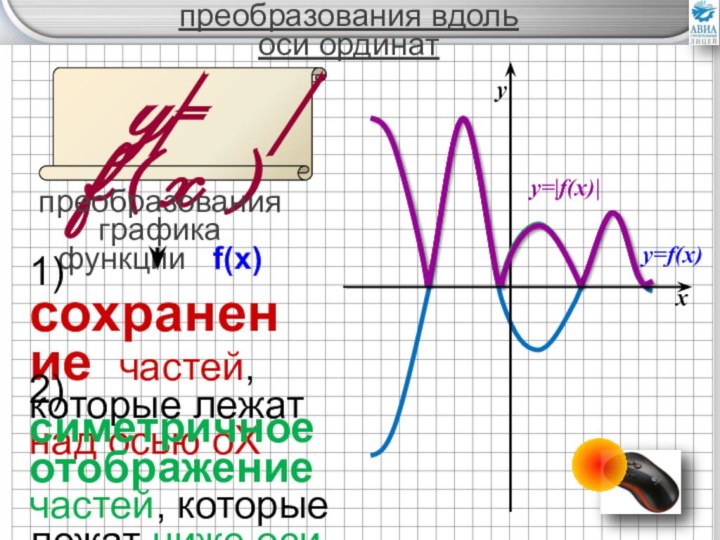
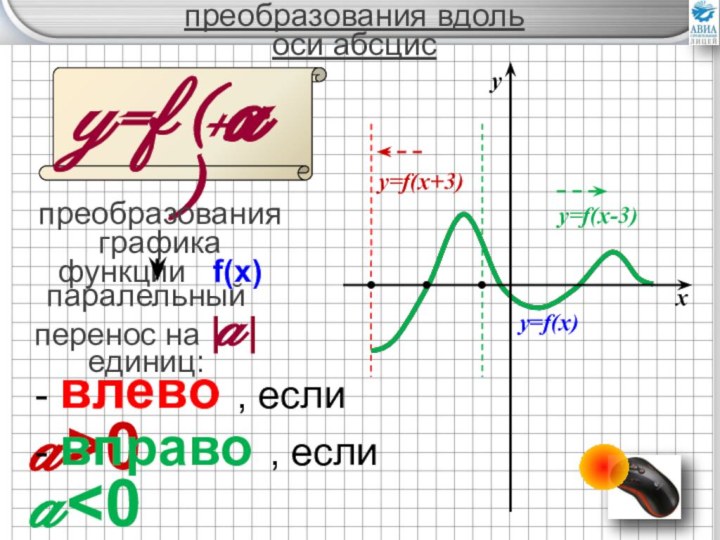
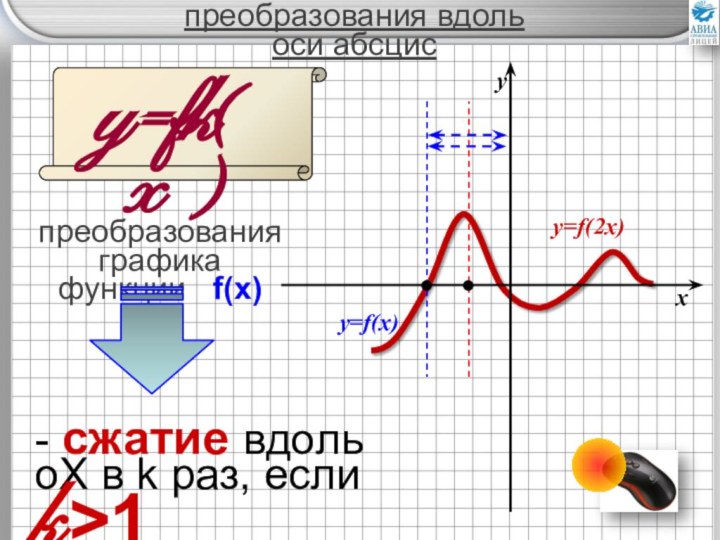
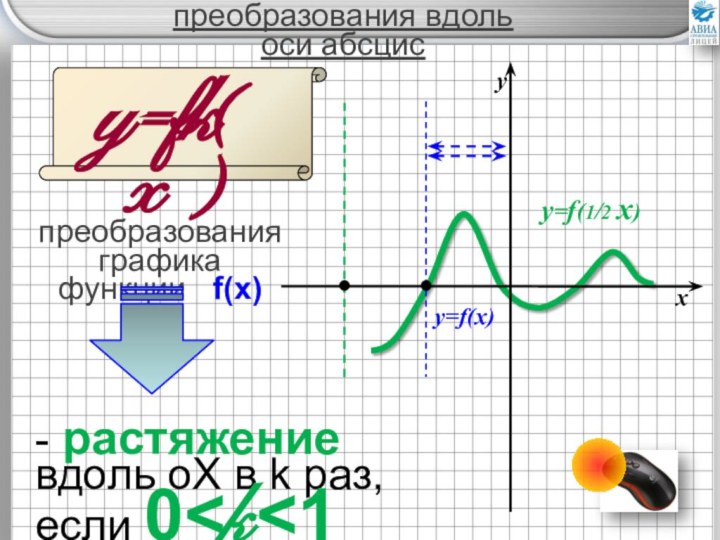
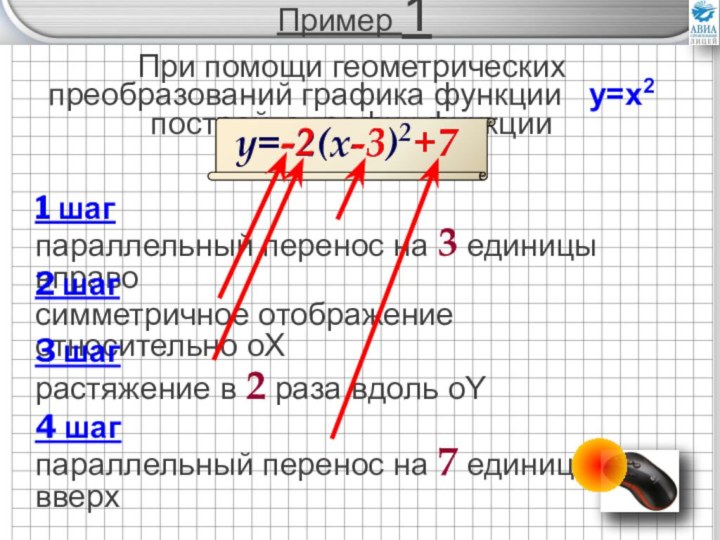
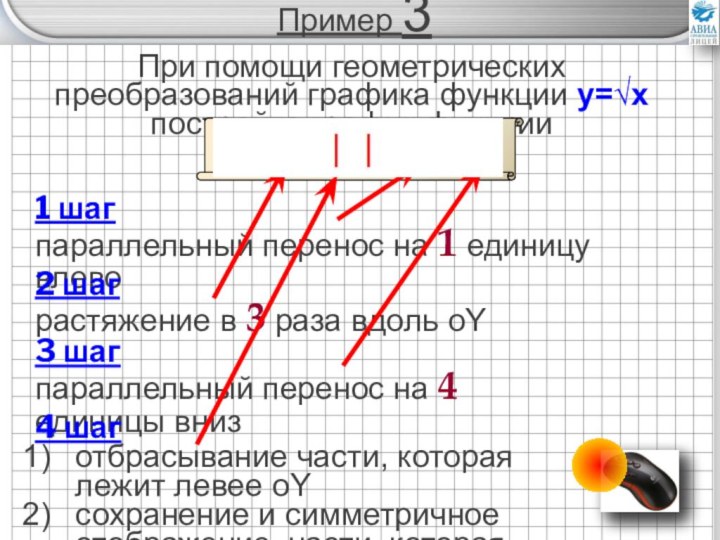
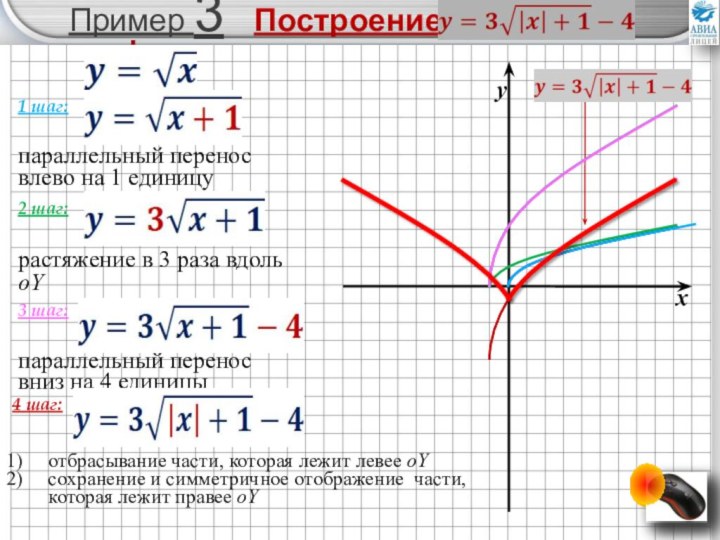
преобразований графиков элементарных функций
Задачи:
Рассмотреть возможные направления преобразований графиков функций.
Изучить,

к каким изменениям в графиках функций приводит появление числовых слагаемых, коэффициентов, знаков модуля в записи формулы функции.
Научиться использовать теоретические сведения об изменениях формы графиков для решения практических задач.
Исследовать нетипичные способы геометрических преобразований для построения графиков функций.
Выработать критерии выбора способа построения графика функции.

абсцисс
x
y
x
y

единиц:
- вверх, если b>0
- вниз, если b

ординат

f(x)
k
- растяжение вдоль oY у k раз, если k>1
x
y
y=2f(x)
y=f(x)
4
8

f(x)
k
x
y
y=f(x)
y=1/2 f(x)
2
4
- сжатие вдоль oY в k раз, если

0

f(x)
k
- симметричное отображение относительно оси абсцисс, если k=-1
x
y
y=f(x)
-4
4
y= -f(x)

f(x)
| |
1) сохранение частей, которые лежат над осью

oX

x

y

y=|f(x)|

y=f(x)

2) симетричное отображение частей, которые лежат ниже оси oX

f(x)
+a
паралельный перенос на |a| единиц:
- влево , если

a>0

- вправо , если a<0

x

y

y=f(x+3)

y=f(x)

y=f(x-3)

f(x)
k
- сжатие вдоль oX в k раз, если k>1
x
y
y=f(2x)
y=f(x)

f(x)
k
- растяжение вдоль oX в k раз, если 0

x)

y=f(x)

оси ординат, если k=-1
x
y
y=f(x)
y= f(-x)
y=f( x)
k
преобразования вдоль оси абсцис

|
1) отбрасывание части, которая лежит левее oY
x
y
y=f(|x|)
y=f(x)
2) сохранение и

симметричное отображение части, которая лежит правее oY

преобразования вдоль оси абсцис

y=x2 постройте график функции

y=-2(x-3)2+7

1 шаг
параллельный перенос на 3 единицы вправо

2 шаг
симметричное отображение относительно oX

3 шаг
растяжение в 2 раза вдоль oY

4 шаг
параллельный перенос на 7 единиц вверх

-

2

+7

-3

шаг:y=-2(x-3)2+7
параллельный перенос вправо на 3 единицы
симметричное отображение относительно oX
растяжение

в 2 раза вдоль oY

параллельный перенос вверх на 7 единиц

x

y

y=-2(x-3)2+7

y=-2(x-3)2+7

y=x2 постройте график функции
y=|x2-6x+4|
Выделим полний квадрат из квадратного трехчлена:
|x2-6x+4|=

|(x2-2.x.3+32)-32+4|=|(x-3)2-5|

Следовательно необходимо построить график функции

y=|(x-3)2-5|

вправо на 3 единицы
параллельный перенос вниз на 5 единиц

сохранение частей, которые лежат над осью oX ;

симметричное отображение частей, которые лежат ниже оси oX

x

y

y=|(x-3)2-5|

y=|(x-3)2-5|

постройте график функции
1 шаг
параллельный перенос на 1 единицу влево
2

шаг
растяжение в 3 раза вдоль oY

3 шаг
параллельный перенос на 4 единицы вниз

4 шаг
отбрасывание части, которая лежит левее oY
сохранение и симметричное отображение части, которая лежит правее oY.

перенос влево на 1 единицу
растяжение в 3 раза вдоль

oY

параллельный перенос вниз на 4 единицы

отбрасывание части, которая лежит левее oY
сохранение и симметричное отображение части, которая лежит правее oY

x

y

функции y=|x+1|
2 шаг: построим график функции y=|x-1|
3 шаг:

y=|x+1|+|x-1|

Ординату искомого графика получаем сложением ординат двух построенных графиков в той самой точке

x

y

y =|x+1|+|x-1|

график функции y=f(x)
1 шаг: Предположим, график функции y=f(x) имеет

такой вид

2 шаг: Построим вертикальные асимптоты для графика y=1/f(x). Они будут проходить через точки пересечения графика y=f(x) и оси oX.

3 шаг: Точки графика y=f(x) с ординатами y=1 и y=-1 будут общими для обоих графиков.

y =1/f(x)

4 шаг: Для точек графика y=f(x) с положительными ординатами соответствующие точки графика y=1/f(x) будут иметь также положительные ординаты, а для отрицательных – отрицательные. Чим больше по модулю ордината точки графика y=f(x), тем в большей мере график y=1/f(x) приближается к оси oX и наоборот.

x

y

и методом деления график функции
и сравним результаты
Выполним преобразования выражения
для

сложения графиков

для деления графиков

y = y1 + y2

y = 1/ y3

y=x
2 шаг: построим график функции y=1/x
3 шаг:
Ординату искомого

графика получим сложением ординат построенных графиков в той самой точке

x

y

Построенный график имеет две асимптоты:
- вертикальную x=0; - наклонную y=x.

график функции
2 шаг: построим вертикальную асимптоту для графика y=1/y3.

Она будет проходить через точку пересечения графика y3=f(x) с осью oX.

3 шаг: график y3=f(x) не имеет точек с ординатами y=1 и y=-1 . Следовательно, общие точки графиков функций y3=f(x) и y=1/y3 отсутствуют.

4 шаг: Для точек графика y3=f(x) с положительными ординатами соответствующие точки графика y=1/y3 будут иметь также положительные ординаты, а для отрицательных – отрицательные. Чем больше по модулю ордината точки графика y3=f(x), тем больше график y=1/y3 приближается к оси oX и наоборот

x

y

y

-1/2

-2

1/2

2

построен сложением, точно определяет еще и наклонную асимптоту. 2)Суммировать

ординаты легче, чем оценивать пропорции их изменения.

Вывод: Для построения графика выбираем тот способ, который обеспечивает более информативный результат и является более удобным в применении.