- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме:Степенная функция и ее график
Содержание
- 2. у = х2у = х3ПараболаКубическая параболаГиперболау = хПрямаяЧастные случаи степенной функции
- 3. Функция вида у = хр,
- 4. Показатель р = 2n – четное натуральное
- 5. yx -1 0 1 у = х2 у = х6
- 6. Показатель р = 2n-1 – нечетное
- 7. yx -1 0 1 у = х3 у = х7
- 8. Показатель р = – 2n, где n
- 9. yx -1 0 1 у = х-2у = х-6
- 10. Показатель р = – (2n-1), где n
- 11. yx -1 0 1 у = х-1у = х-5
- 12. 0Показатель р – положительное действительное нецелое число1хуу
- 13. yx -1 0 1 у = х0,5
- 14. yx -1 0 1
- 15. 0Показатель р – отрицательное действительное нецелое число1хуу
- 16. yx -1 0 1
- 17. Пользуясь рисунком, найти промежутки, на которых график
- 18. Пользуясь рисунком, найти промежутки, на которых график
- 19. Пользуясь рисунком, найти промежутки, на которых график
- 20. yx -1 0 1 у = (х + 2)-6
- 21. yx -1 0 1 у = х– 6 – 4
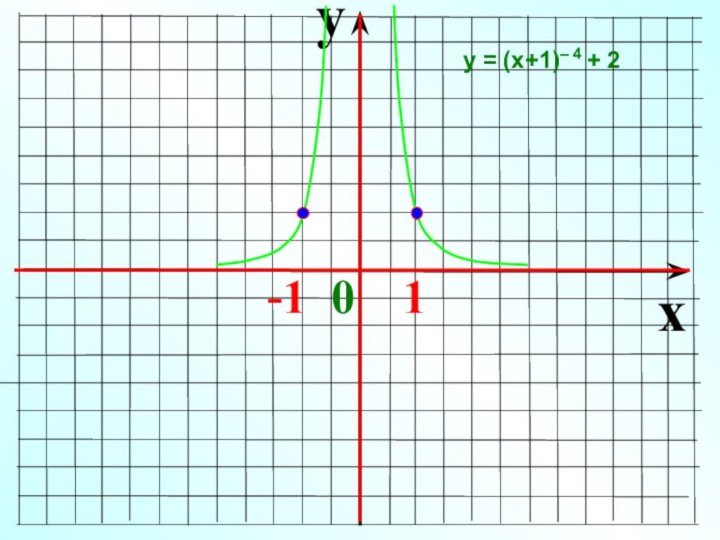
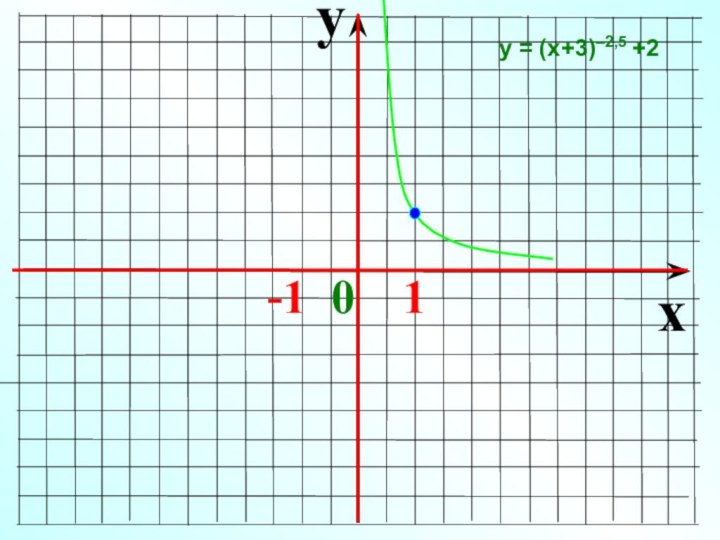
- 22. yx -1 0 1 у = (х+1)– 4 + 2
- 23. yx -1 0 1 у = (х-3)– 3+1
- 24. Скачать презентацию
- 25. Похожие презентации
у = х2у = х3ПараболаКубическая параболаГиперболау = хПрямаяЧастные случаи степенной функции















Слайд 3 Функция вида у = хр, где
р – действительное число называется степенной функцией
Свойства и график
степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень
Слайд 4
Показатель р = 2n – четное натуральное число
1
0
х
у
у
= х2, у = х4 ,
у = х6, у = х8, …у = х2
Функция у=х2n четная,
т.к. (–х)2n = х2n
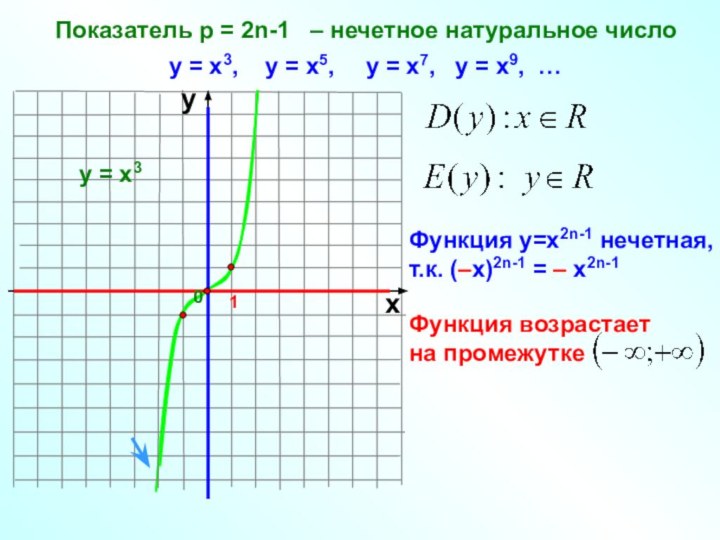
Слайд 6 Показатель р = 2n-1 – нечетное натуральное
число
1
х
у
у = х3, у = х5,
у = х7, у = х9, … у = х3
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
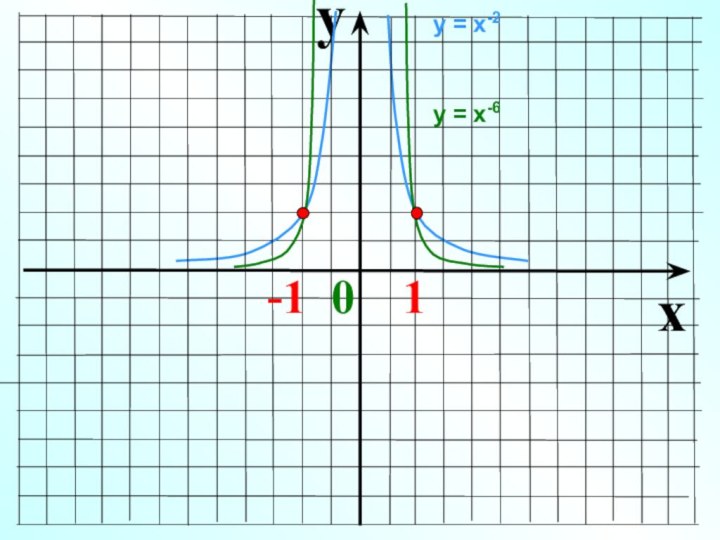
Слайд 8 Показатель р = – 2n, где n –
натуральное число
1
0
х
у
у = х-2, у = х-4 ,
у = х-6, у = х-8, … Функция у=х2n четная,
т.к. (–х)-2n = х-2n
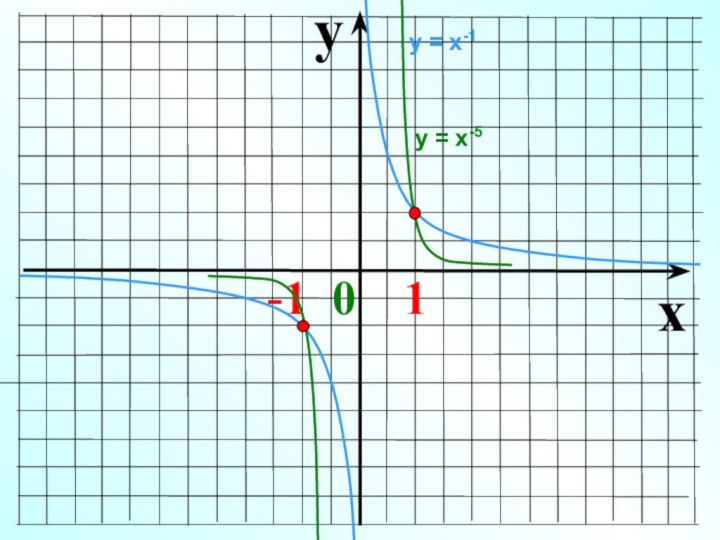
Слайд 10 Показатель р = – (2n-1), где n –
натуральное число
1
0
х
у
у = х-3, у = х-5 ,
у = х-7, у = х-9, … Функция у=х-(2n-1) нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
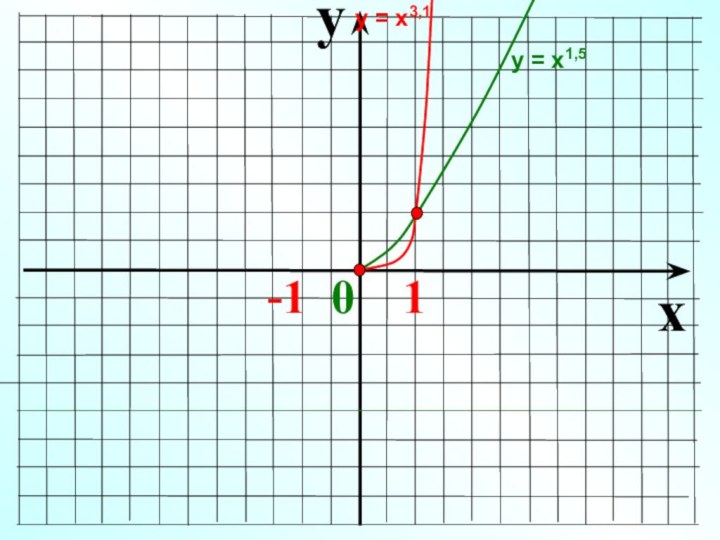
Слайд 12
0
Показатель р – положительное действительное нецелое число
1
х
у
у =
х1,3, у = х0,7, у
= х2,12, …
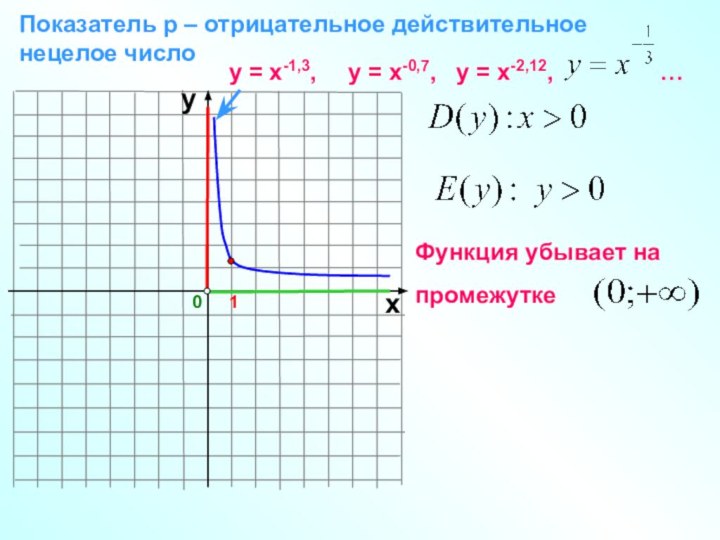
Слайд 15
0
Показатель р – отрицательное действительное
нецелое число
1
х
у
у =
х-1,3, у = х-0,7, у
= х-2,12, …
Слайд 17
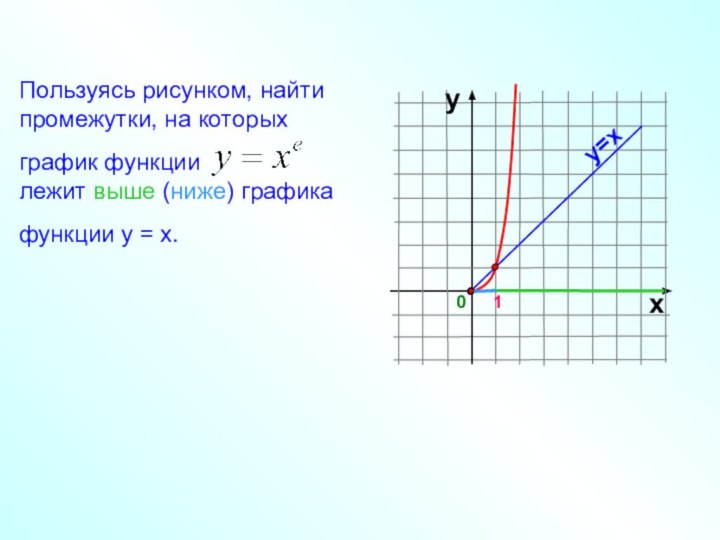
Пользуясь рисунком, найти промежутки, на которых
график функции
лежит выше (ниже) графика
функции у = х.
0
1
х
у
у=х
Слайд 18
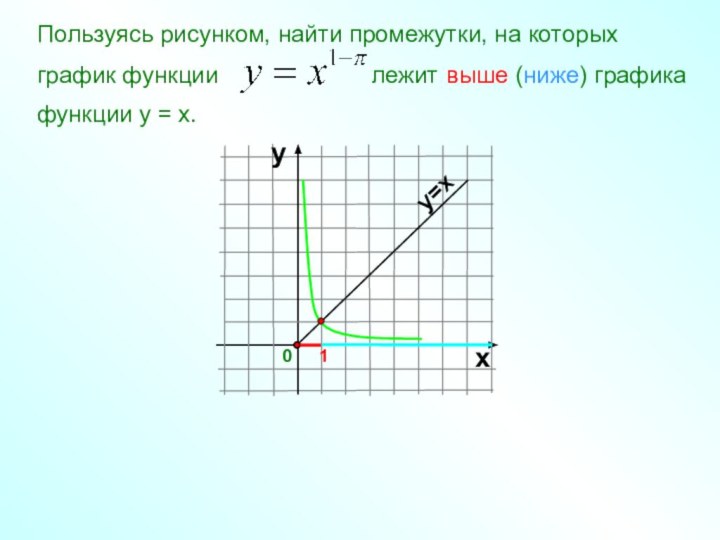
Пользуясь рисунком, найти промежутки, на которых
график функции
лежит выше (ниже) графика
функции у = х.
у
0
1
х
у=х
Слайд 19
Пользуясь рисунком, найти промежутки, на которых
график функции
лежит выше (ниже) графика
функции у = х.





























