- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Решение неравенств методом интервалов
Содержание
- 2. Устная работа:1.Разложить на множители:х2 -1х2 -1213х-48х2 -5х+6
- 3. 2. Найти нули функции:а)у=х-6 б)у=х+5в) у=х2-9 г)у=(х-4)(х+3)д)у=х(х-10)е)у=х2-2х+1
- 4. Актуализация опорных знанийРешить неравенства:1)2х-3(х-7)
- 5. Проблема! Не умеем решать неравенства вида:(х-а)(х-в)…(х-n)0 Используется метод интервалов. Наша задача:Научиться решать неравенства методом интервалов.
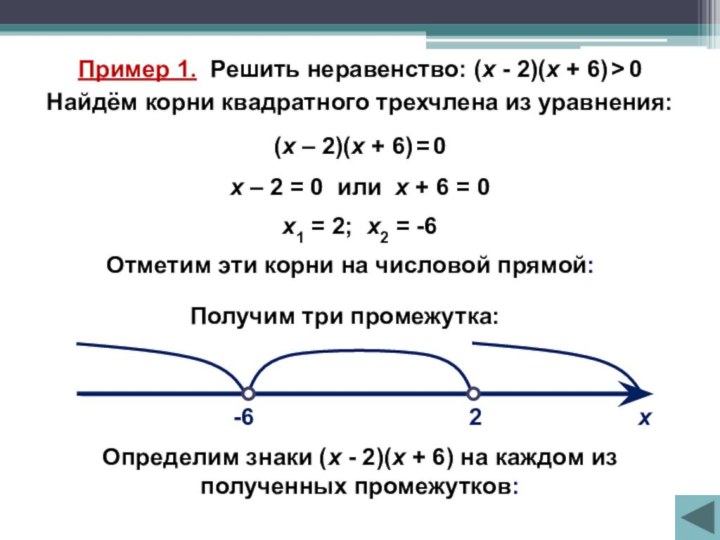
- 6. Пример 1. Решить неравенство: (х - 2)(х
- 7. 2-6х1). (х - 2)(х + 6) =
- 8. №325(а,в)
- 9. Пример 2. Решить неравенство: 2х2 - 3х
- 10. +10,5х1). 2х2 - 3х + 1 =
- 11. Пример 3. Решить неравенство: -х2 + х
- 12. +–4-3х1). -х2 + х + 12 =
- 13. Скачать презентацию
- 14. Похожие презентации










Слайд 5
Проблема!
Не умеем решать неравенства вида:
(х-а)(х-в)…(х-n)
(х-а)(х-в)…(х-n)>0
Используется метод интервалов.
Наша задача:
Научиться решать неравенства
методом интервалов.Слайд 6 Пример 1. Решить неравенство: (х - 2)(х +
6) > 0
Найдём корни квадратного трехчлена из уравнения:
(х
– 2)(х + 6) = 0х1 = 2; х2 = -6
Отметим эти корни на числовой прямой:
2
-6
х
Получим три промежутка:
Определим знаки (х - 2)(х + 6) на каждом из полученных промежутков:
х – 2 = 0 или х + 6 = 0
Слайд 7
2
-6
х
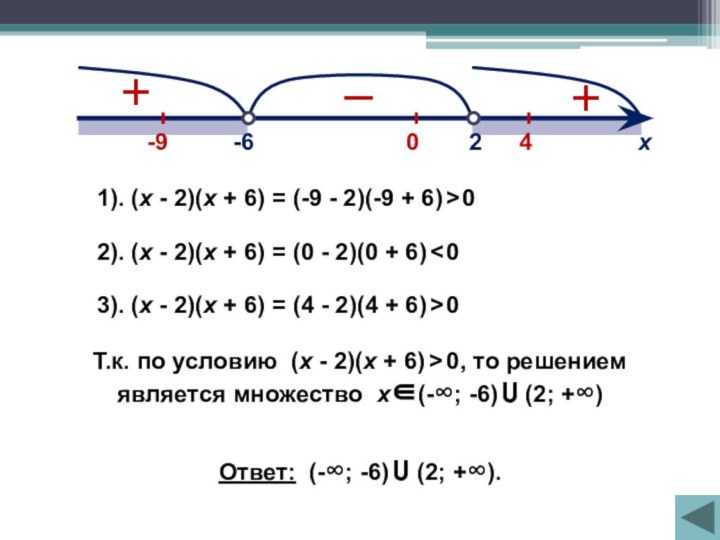
1). (х - 2)(х + 6) = (-9
- 2)(-9 + 6) > 0
-9
2). (х -
2)(х + 6) = (0 - 2)(0 + 6) < 0 0
4
3). (х - 2)(х + 6) = (4 - 2)(4 + 6) > 0
+
+
–
Т.к. по условию (х - 2)(х + 6) > 0, то решением
является множество х(-∞; -6) U (2; +∞)
Ответ: (-∞; -6) U (2; +∞).
Слайд 9 Пример 2. Решить неравенство: 2х2 - 3х +
1 < 0
Найдём корни квадратного трехчлена из уравнения:
2х2
- 3х + 1 = 0х1 = 1; х2 = 0,5
Отметим эти корни на числовой прямой:
1
0,5
х
Получим три промежутка:
Определим знаки 2х2 - 3х + 1 на каждом из полученных промежутков:
Слайд 10
+
1
0,5
х
1). 2х2 - 3х + 1 = 2∙02
- 3∙0 + 1 > 0
0
0,8
1,2
+
–
Т.к. по условию
2х2 - 3х + 1 < 0, то решением является множество х(0,5; 1)
Ответ: (0,5; 1).
2). 2х2 - 3х + 1 = 2∙0,82 - 3∙0,8 + 1 < 0
3). 2х2 - 3х + 1 = 2∙1,22 - 3∙1,2 + 1 > 0
Слайд 11 Пример 3. Решить неравенство: -х2 + х +
12 ≥ 0
Найдём корни квадратного трехчлена из уравнения:
-х2
+ х + 12 = 0х1 = 4; х2 = -3
Отметим эти корни на числовой прямой:
4
-3
х
Получим три промежутка:
Определим знаки -х2 + х + 12 на каждом из полученных промежутков:
Слайд 12
+
–
4
-3
х
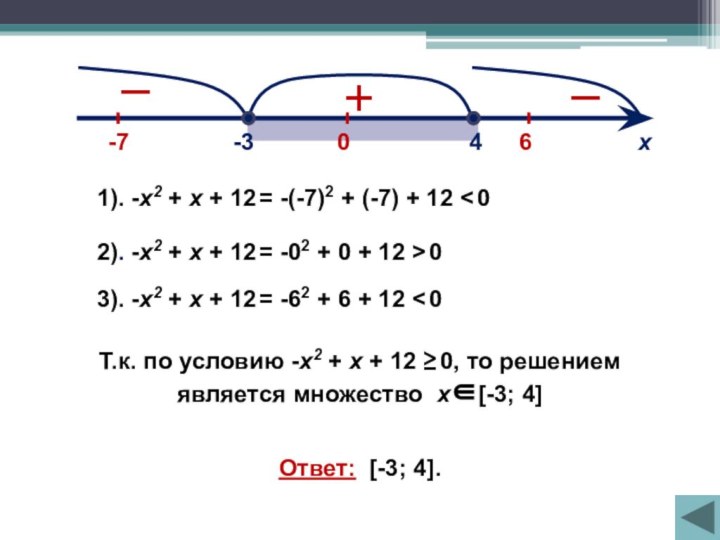
1). -х2 + х + 12 = -(-7)2
+ (-7) + 12 < 0
-7
0
6
–
Т.к. по условию
-х2 + х + 12 ≥ 0, то решением является множество х[-3; 4]
Ответ: [-3; 4].
2). -х2 + х + 12 = -02 + 0 + 12 > 0
3). -х2 + х + 12 = -62 + 6 + 12 < 0





























