- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подготовка к ОГЭ. Линейные и квадратичные функции.
Содержание
- 2. Тема урока: «Подготовка к ОГЭ.Линейная и квадратичная функции»22.04.2016
- 3. Область определения функции – (-2; 5]это все значения независимой переменной xху
- 4. Функция задана графиком.Укажите область определения этой функции.1
- 5. Область значений функции – (-5; 7)хуэто все значения зависимой переменной у
- 6. 1 2 3 4
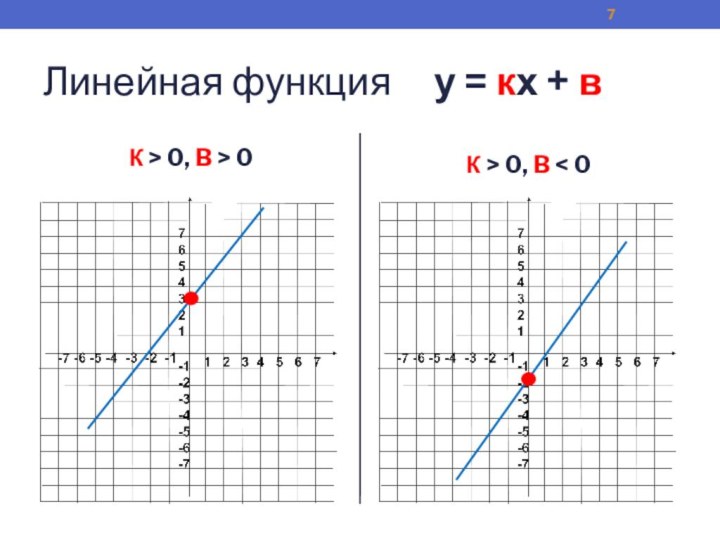
- 7. Линейная функция у = кх
- 8. Линейная функция у=кх+вК < 0, B > 0К < 0, B < 0
- 9. Прямая пропорциональностьK > 0K < 0 у = кх
- 10. Линейная функция у= bB > 0B < 0
- 11. Линейная функция x= bB > 0B < 0
- 13. На рисунке изображены графики функций вида у=kx+b.
- 16. y= ax2 +bx + cгде: a,b,c –
- 17. Определим знаки коэффициентов квадратичной функциив зависимости от поведения параболыy= ax2 +bx + c
- 18. ветви параболы направлены вверх, при
- 19. y= ax2 +bx + cЗнак последнего коэффициента
- 20. Знак второго коэффициента b можно определить, используя
- 21. Способ вершины параболы (СВП)
- 22. Способ вершины параболы (СВП)
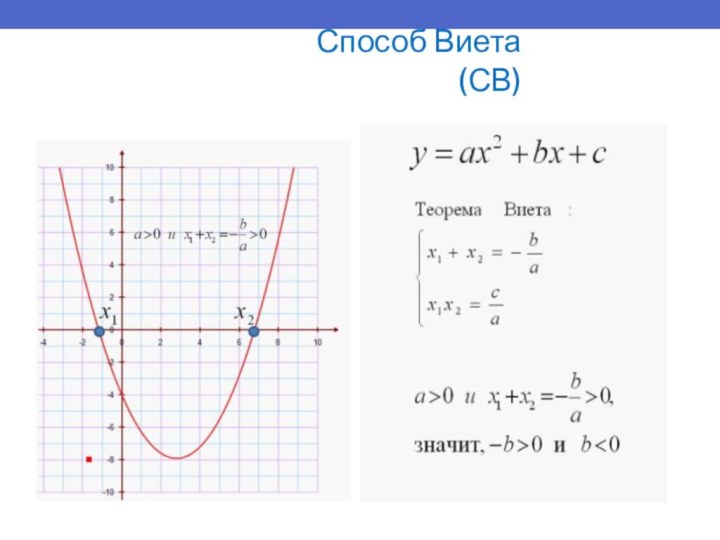
- 23. Способ Виета (СВ)
- 24. Способ Виета (СВ)
- 27. зная направление ветвей параболы и знак дискриминанта,
- 28. если дискриминант больше нуля, то парабола
- 29. На рисунке изображены графики функций вида y=
- 31. Установите соответствие между функциями и их графиками. А) Б) В)
- 33. Ответы:Вариант 1Вариант 2
- 36. Любая точка параболы равноудалена от некоторой
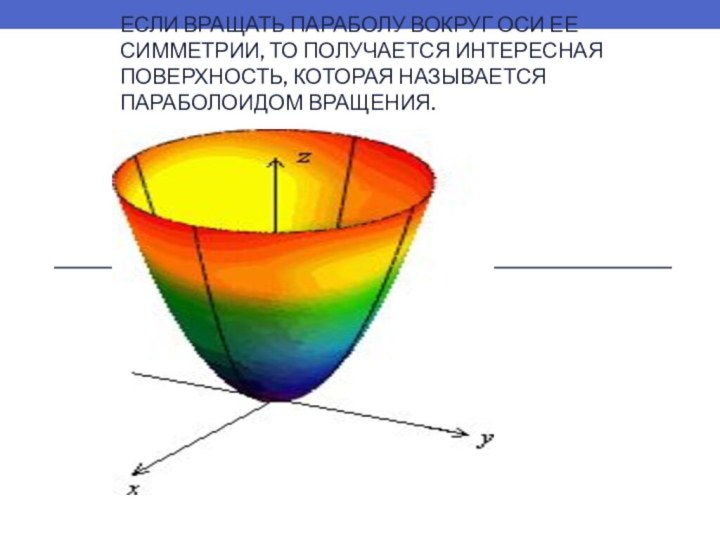
- 37. Если вращать параболу вокруг оси ее симметрии, то получается интересная поверхность, которая называется параболоидом вращения.
- 38. Траектории некоторых космических тел (комет,
- 41. Скачать презентацию
- 42. Похожие презентации


![Презентация: Подготовка к ОГЭ. Линейные и квадратичные функции. Область определения функции – (-2; 5]это все значения независимой переменной xху](/img/tmb/6/561959/2aaf0fcefa55494063732cc786614d4e-720x.jpg)































Слайд 4
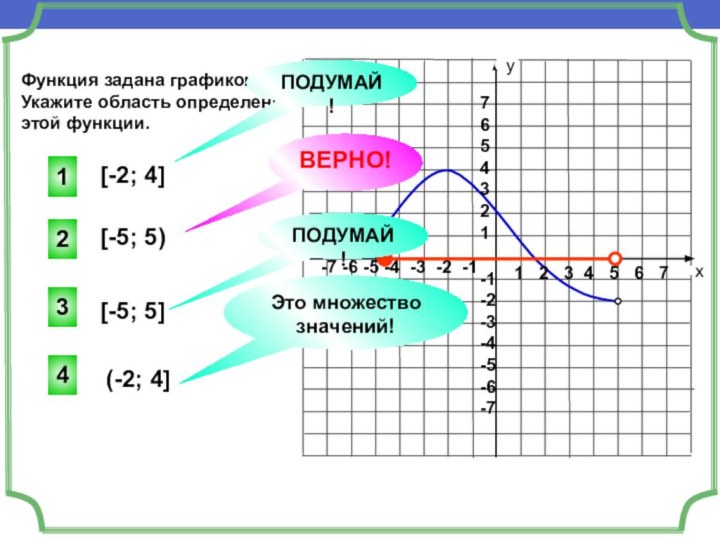
Функция задана графиком.
Укажите область определения
этой функции.
1
2 3 4 5 6
7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
[-2; 4]
[-5; 5)
[-5; 5]
(-2; 4]
2
1
3
4
ПОДУМАЙ!
ВЕРНО!
Это множество значений!
ПОДУМАЙ!
у
х
Слайд 6 1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком.
Укажите область значений
этой функции.
[1; 6]
[-6; 5)
[-2; 6]
(-2; 6]
4
ВЕРНО!
1
3
2
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
у
х
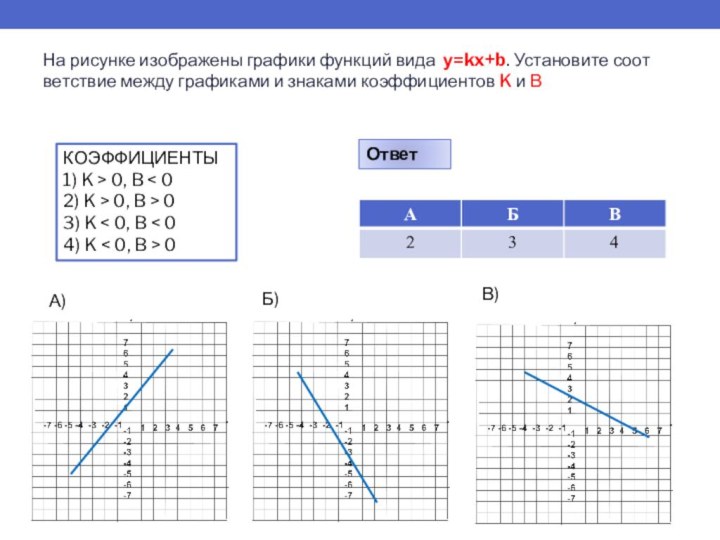
Слайд 13 На рисунке изображены графики функций вида у=kx+b. Установите
соответствие между графиками и знаками коэффициентов K и В
КОЭФФИЦИЕНТЫ
1)
K > 0, B < 02) K > 0, B > 0
3) K < 0, B < 0
4) K < 0, B > 0
Ответ
А)
Б)
В)
Слайд 16
y= ax2 +bx + c
где: a,b,c –
числа
х– независимая переменная
а 0Определение квадратичной функции
Квадратичной функцией называется функция , которую можно задать формулой вида:
Слайд 17
Определим знаки коэффициентов квадратичной функции
в зависимости от поведения
параболы
y= ax2 +bx + c
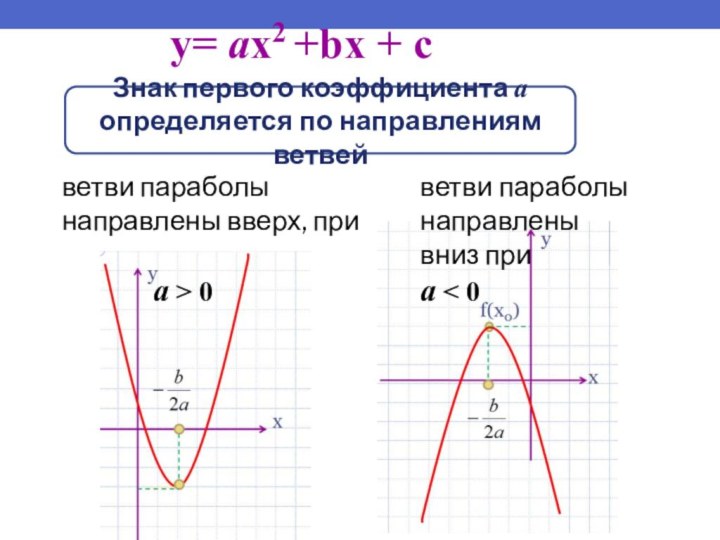
Слайд 18
ветви параболы направлены вверх, при
ветви параболы направлены вниз при
a < 0
y= ax2 +bx + c
Знак первого коэффициента a определяется по направлениям ветвей
Слайд 19
y= ax2 +bx + c
Знак последнего коэффициента с
определяется точкой пересечения параболы с осью Оу!
Это вытекает из
очевидного равенства у(0)=с
с < 0
с > 0
с = 0
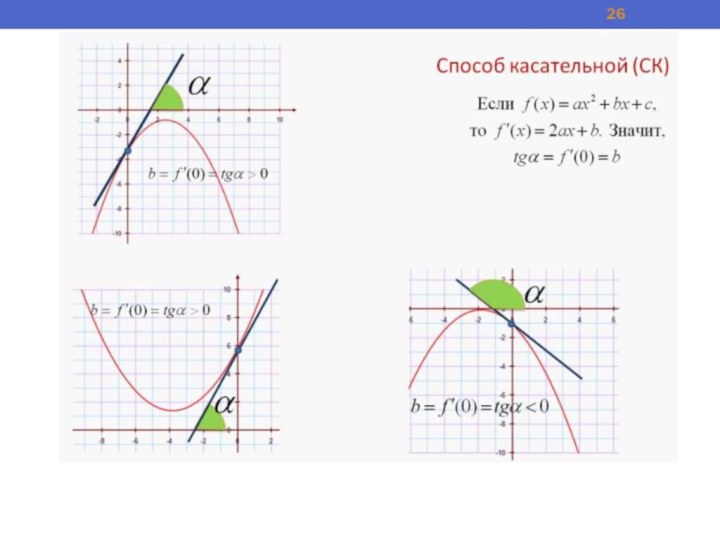
Слайд 20 Знак второго коэффициента b можно определить, используя разные
способы:
1. Способ вершины параболы (СВП)
2. Способ Виета (СВ) 3. Способ касательной (СК)
y= ax2 +bx + c
Слайд 27 зная направление ветвей параболы и знак дискриминанта, мы
уже можем в общих чертах определить, как выглядит график
нашей функции.
Слайд 28
если дискриминант больше нуля, то парабола
если дискриминант равен нулю, то парабола
если дискриминант
меньше нуля, то Многие свойства квадратичной функции
зависят от значения дискриминанта.
пересекает ось абсцисс в двух точках;
касается оси абсцисс;
парабола не пересекает ось абсцисс;
Слайд 29 На рисунке изображены графики функций вида y= ax2
+bx + c. Для каждого графика укажите соответствующее ему
значения коэффициента a и дискриминанта DОтвет





























