чисел поставлено в соответствие число у, то говорят, что
на этом множестве задана функция у(х).y = f(x)
При этом х называют независимой переменной или аргументом,
а у – зависимой переменной или функцией.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Числовая Функция (10 класс)
Содержание
- 2. Понятие функцииЕсли каждому значению х из некоторого
- 3. Область определения и множество значений функцииОбластью определения
- 4. График функцииГрафиком функции называется множество всех точек
- 5. ОПРЕДЕЛЕНИЕ ЧИСЛОВОЙ ФУНКЦИИ И СПОСОБЫ ЕЕ ЗАДАНИЯ
- 6. 2. Какие из графиков, изображенных на рисунках, являются графиками функций?
- 8. xy0Y = f(x)Y = - f(x)ОСНОВНЫЕ ПРАВИЛА
- 9. xy0Y = f(x)Y = f(x – a),
- 10. ху0Y = f(x)Y = f(x) + b,
- 11. ухУ = f(x)Y = f(kx), 0 <
- 12. ух0У = kf(x), 0 < k <
- 13. yx0yx0У = If(x)I8. У = If(x)I –
- 14. Скачать презентацию
- 15. Похожие презентации
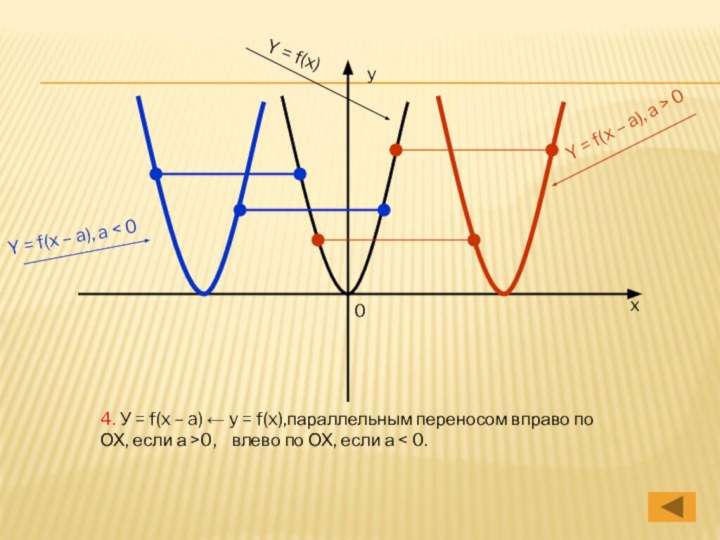
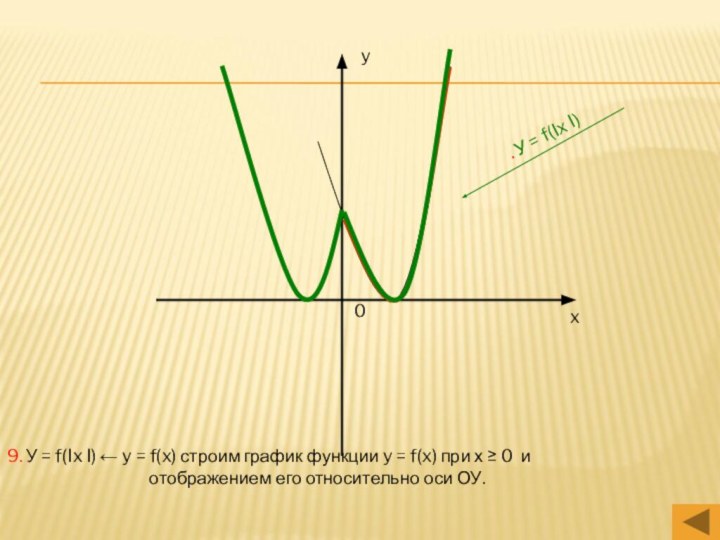
Понятие функцииЕсли каждому значению х из некоторого множества чисел поставлено в соответствие число у, то говорят, что на этом множестве задана функция у(х). y = f(x)При этом х называют независимой переменной или аргументом, а у –
Слайд 2
Понятие функции
Если каждому значению х из некоторого множества
Слайд 3
Область определения и
множество значений функции
Областью определения функции
называют множество всех значений, которые может принимать ее аргумент.
Обозначается
D(y)Множество значений (или область значений) функции – это множество всех значений переменной у.
Обозначается E(y)
Слайд 4
График функции
Графиком функции называется множество всех точек координатной
плоскости (х; у(х)), абсциссы которых равны значениям независимой переменной
из области определения этой функции, а ординаты – соответствующим значениям функции.x (абсцисса)
(ордината) y
y = f(x)
0
Слайд 8
x
y
0
Y = f(x)
Y = - f(x)
ОСНОВНЫЕ ПРАВИЛА ПРЕОБРАЗОВАНИЯ
ГРАФИКОВ ФУНКЦИЙ
1. У = - f(x) ← y =
f(x) , отображением относительно оси ОХ.2. У = f(- x) ← y = f(x), отображением от оси ОУ.
3. У = - f (- x) ← y = f(x), отображением относительно начала координат.
Слайд 9
x
y
0
Y = f(x)
Y = f(x – a), a
< 0
Y = f(x – a), a > 0
4.
У = f(x – a) ← y = f(x),параллельным переносом вправо по ОХ, если а >0, влево по ОХ, если а < 0.
Слайд 10
х
у
0
Y = f(x)
Y = f(x) + b, b
> 0
Y = f(x) + b, b < 0
5.
У = f(x) + b ← y = f(x), параллельным переносом вверх по ОУ, если в > 0, вниз по ОУ, если в < 0.
Слайд 11
у
х
У = f(x)
Y = f(kx), 0 < k
< 1
Y = f(kx), k > 1
0
6. У =
f(kx) ← y = f(x), растяжением в вдоль оси ОХ в 1/к раз, если 0 < к < 1; сжатием вдоль оси ОХ в к раз, если к > 1.
Слайд 12
у
х
0
У = kf(x), 0 < k < 1
Y
= kf(x), k > 1
Y = kf(x), 0
k < 17. У = kf(x) ← y = f(x), сжатием вдоль оси ОУ в 1/к раз, если 0 < к < 1 и
растяжением вдоль оси ОУ в к раз, если к > 1.
Слайд 13
y
x
0
y
x
0
У = If(x)I
8. У = If(x)I – совпадает
