- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Наибольшее и наименьшее значения функции. (11 класс)
Содержание
- 2. 1 вариант
- 3. 1 вариант
- 21. Использование неравенств:a+1/a ≥2 при всех а>0a+1/a =2 при а=1
- 22. Задача: Найти наименьшее значение функции: F(x) =(X4-4x3+8x2-8x+5)/(x2-2x+2)
- 23. Решение:F(x) =(X2-2x+2)2 + 1)/(x2-2x+2)F(x) =X2-2x+2 + 1/(x2-2x+2)
- 24. Векторный способ решения
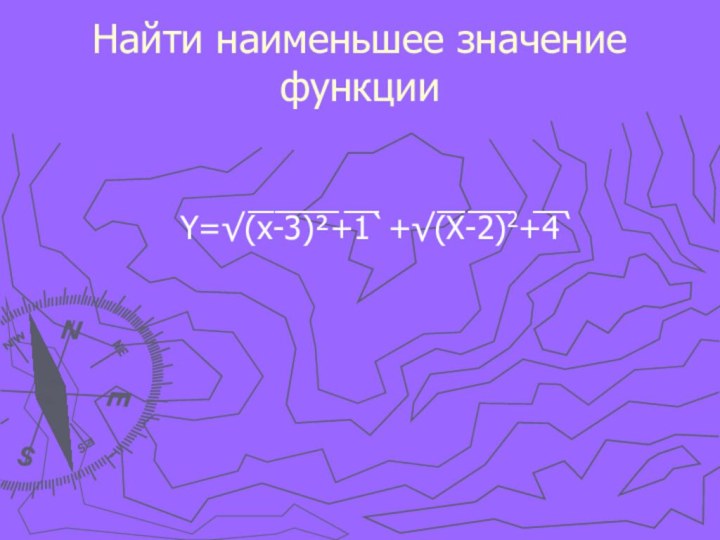
- 25. Найти наименьшее значение функцииY=√(̅x̅-̅3̅)̅²̅+̅1̅`+√(̅X̅-̅2̅)̅2+̅4̅`
- 26. Решение:Введем векторы ā{3-X;1} и b̅{X-2;2}Тогда |ā|=√(̅x̅-̅3̅)̅²̅+̅1̅`; |b̅|=√(̅X̅-̅2̅)̅2+̅4̅`.(ā+ b̅)={1;3}.|ā+b̅|=√1̅̅²̅ ̅+̅3̅²̅`=√1̅0̅`.Воспользуемся неравенством:|ā|+|b̅|≥ |ā+b̅|
- 27. Имеем:Y=|ā|+|b̅|≥ |ā+b̅|=√1̅0̅`.То есть наименьшее значение функции: √1̅0̅`.
- 28. Геометрический способ решенияНайти наименьшее значение функции:Решение:23Данная функция
- 29. Различные способы нахождения наибольшего и наименьшего значений
- 30. Скачать презентацию
- 31. Похожие презентации
1 вариант 2 вариант




























Слайд 23
Решение:
F(x) =(X2-2x+2)2 + 1)/(x2-2x+2)
F(x) =X2-2x+2 + 1/(x2-2x+2) ≥2
(>0)
(>0)F(x) =2 – наименьшее, если: x2-2x+2=1
x2-2x+1=0
x=1
Значит: F(1) = 2
Ответ: 2.
Слайд 26
Решение:
Введем векторы ā{3-X;1} и b̅{X-2;2}
Тогда |ā|=√(̅x̅-̅3̅)̅²̅+̅1̅`; |b̅|=√(̅X̅-̅2̅)̅2+̅4̅`.
(ā+ b̅)={1;3}.
|ā+b̅|=√1̅̅²̅
̅+̅3̅²̅`=√1̅0̅`.
Воспользуемся неравенством:|ā|+|b̅|≥ |ā+b̅|
Слайд 28
Геометрический способ решения
Найти наименьшее значение функции:
Решение:
2
3
Данная функция задаёт
длину ломаной ACB (см. рисунок), которая будет
наименьшей, если точки
A, C, B лежат на одной прямой. Тогда AMC подобен BKC, поэтому
Ответ: 7.
Слайд 29
Различные способы нахождения наибольшего и наименьшего значений
функции
С помощью
производной
Оценка
Замена переменной
Графический образ
Введение вспомогательного угла
Использование свойств монотонных функций
Введение параметра
С
помощью неравенствВекторный способ
Геометрический способ