- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Графики улыбаются (9 класс)
Содержание
- 2. ЦельСоздание учащимся условий для обоснованного выбора профиля
- 3. ЗадачиЗакрепить основы знаний о построении графиков функцийУглубить
- 4. Графический способ - один из самых удобных
- 5. Графики к различным ситуациям-Мяч подняли над полом
- 6. График функции y=f(x)+ k получается параллельным переносом
- 7. График функции y=f(x+с) получается параллельным переносом графика
- 8. График функции y=аf(x),(а >0) получается растяжением графика
- 9. График функции y=f(kx) получается сжатием графика функции
- 10. График функции y=-f(x) получается симметричным отображением графика функции y=f(x) относительно оси OX.y=3x2y=3x+2y=2x²8x+6y=2x²+8x6
- 11. График функции y=f(-x) получается симметричным отображением графика функции y=f(x) относительно оси OY.y=3x2y=3x2y=корень из -2x+3y=корень из 2x+3
- 12. Построение графиков, содержащих несколько преобразованийy=2(х-3)²+4y=x²→y=(x3)²→y=2(x3)²→y=2(x3)²→y=2(x3)²+4y=2+3/(х-4)y=3/х →y=3/(x4)→y=2+3/(x4)
- 13. График функции y=If(x)I получается из графика функции
- 14. График функции y=f(|x|) получается из графика функции
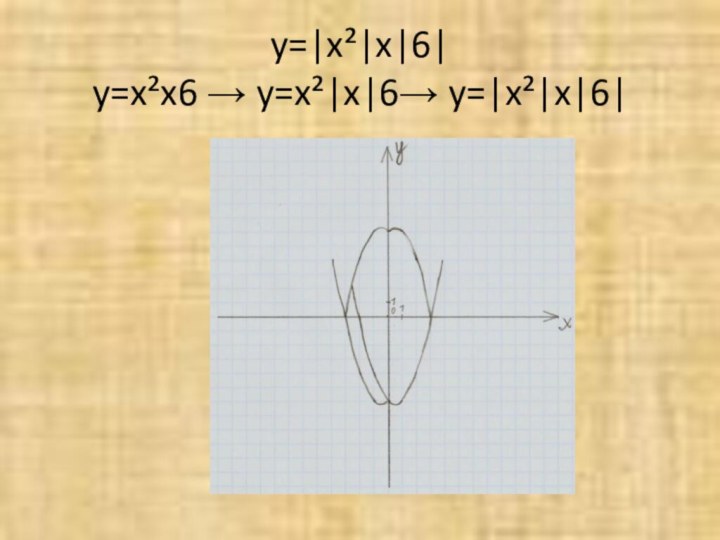
- 15. y=|x²|x|6| y=x²x6 → y=x²|x|6→ y=|x²|x|6|
- 16. График зависимости |y|=f(x) получается из графика y=f(x),
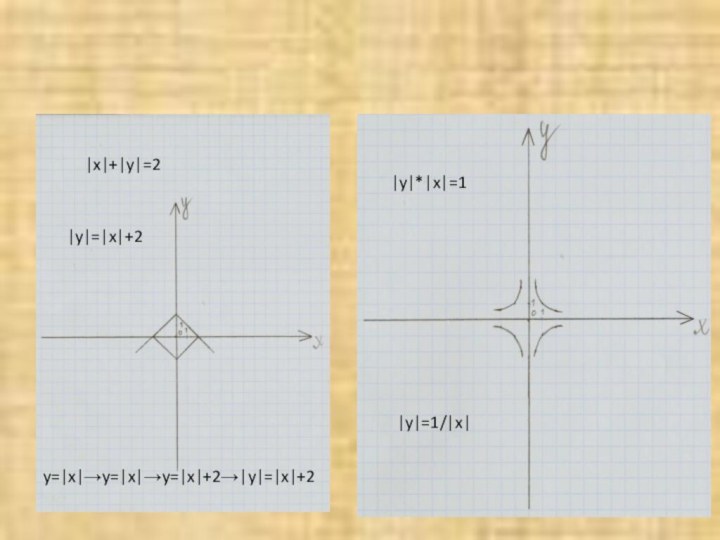
- 17. |x|+|y|=2|y|=|x|+2|y|*|x|=1|y|=1/|x|y=|x|→y=|x|→y=|x|+2→|y|=|x|+2
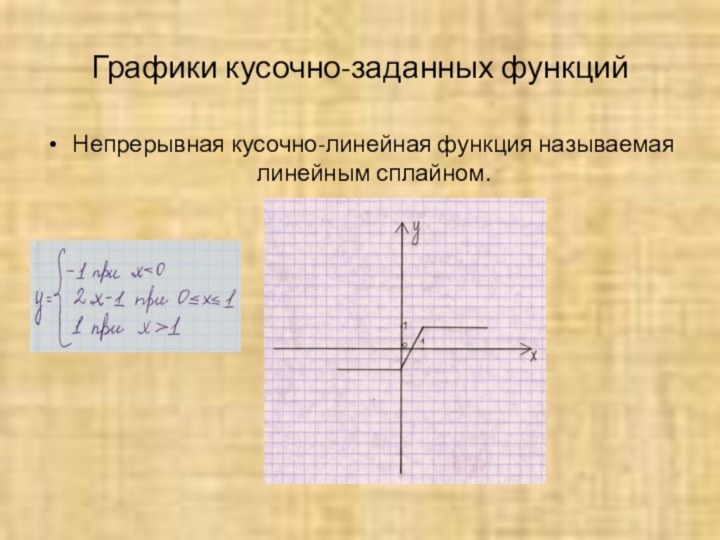
- 19. Графики кусочно-заданных функцийНепрерывная кусочно-линейная функция называемая линейным сплайном.
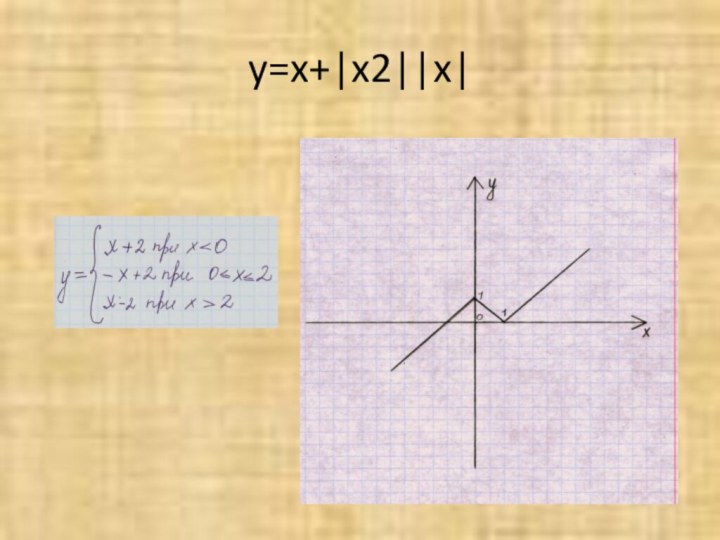
- 20. y=x+|x2||x|
- 21. Кусочно-элементарные функции, не имеющие разрывов.
- 22. Кусочно-элементарные функции с разрывами
- 25. Скачать презентацию
- 26. Похожие презентации
ЦельСоздание учащимся условий для обоснованного выбора профиля обучения через оценку собственных возможностей в усвоении математического материала на основе расширения представления о графиках функции













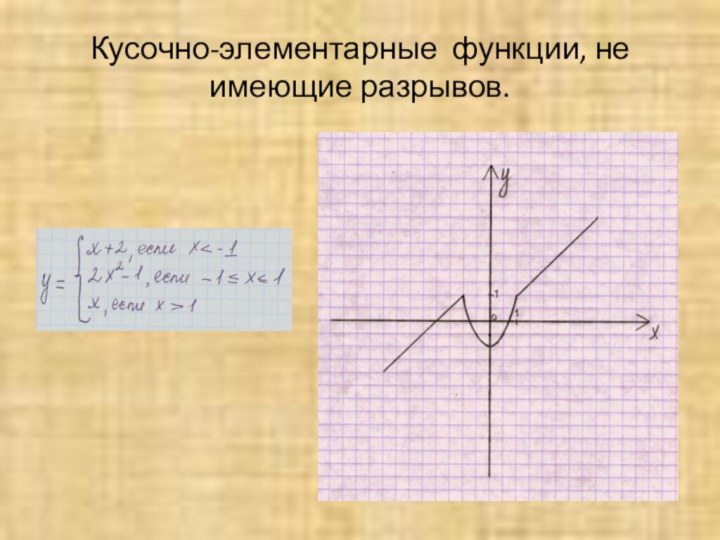

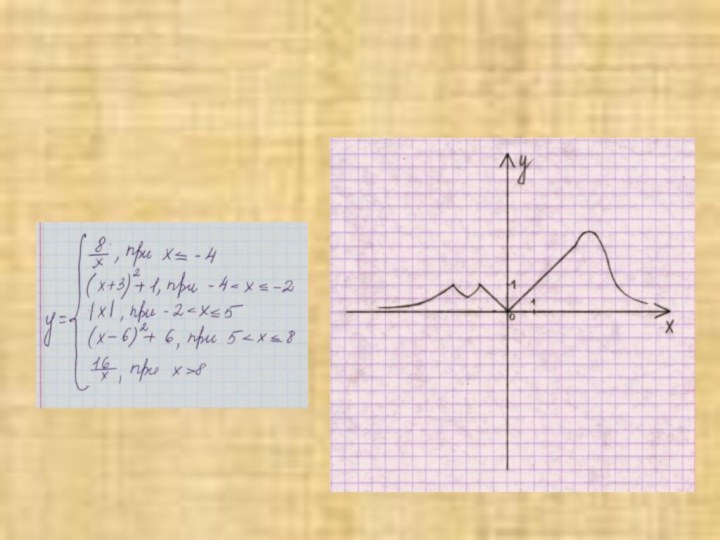

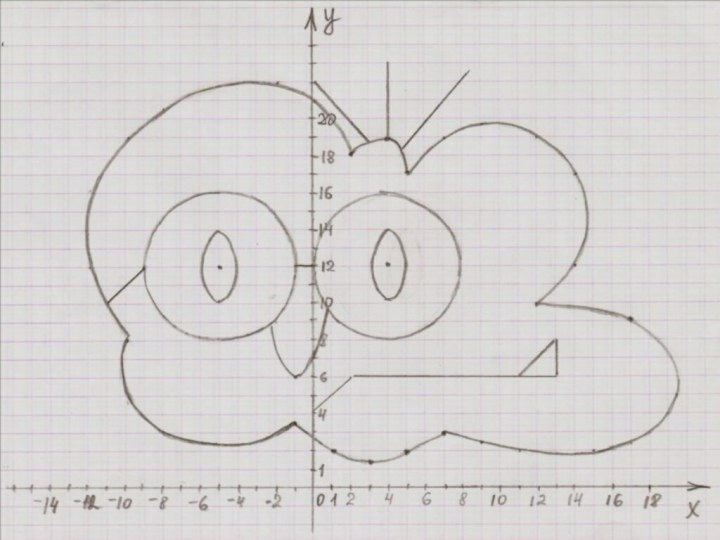
Слайд 3
Задачи
Закрепить основы знаний о построении графиков функций
Углубить и
расширить знания о графиках, выходящих за рамки программы
Вовлечь в
практическую деятельность как фактор личностного развитияСлайд 4 Графический способ - один из самых удобных и
наглядных способов представления и анализа информации.
1.Метеорологическая служба
2.Врачи-болезни сердца(кардиограммы)
3.Геологи- колебания
почвы, показания сейсмографов4.Экономисты-кривые спроса и предложения, линии производственных возможностей
Слайд 5
Графики к различным ситуациям
-Мяч подняли над полом и
выпустили из рук
-Через каждый час
рабочего времени на
склад
сдают изготовленные детали
-Гриб растет, затем его срывают и сушат
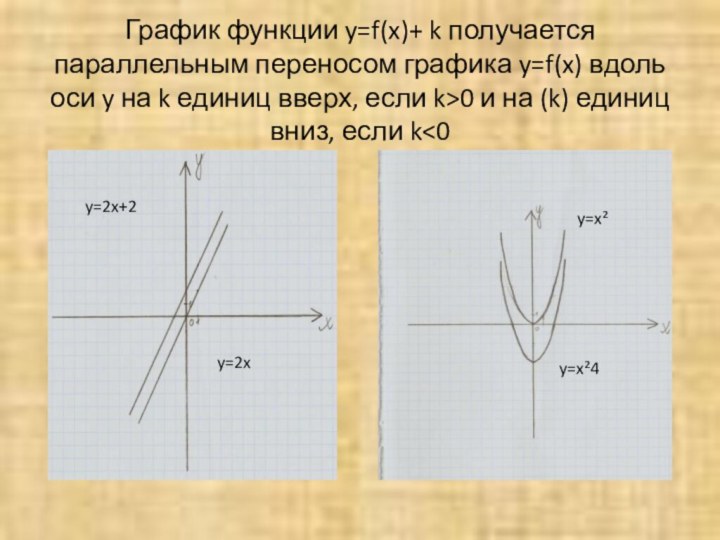
Слайд 6 График функции y=f(x)+ k получается параллельным переносом графика
y=f(x) вдоль оси y на k единиц вверх, если
k>0 и на (k) единиц вниз, если k<0y=x²
y=x²4
y=2x+2
y=2x
Слайд 7 График функции y=f(x+с) получается параллельным переносом графика функции
y=f(x) вдоль оси x на c единиц влево при
с>0 и вправо при с<0y=(x+3)³
y=x³
y=6/x
y=6/(x4)
Слайд 8 График функции y=аf(x),(а >0) получается растяжением графика функции
y=f(x) вдоль оси OY в а раз при а
>1 и сужением в 1/а раз при 0y=3x
y=x
y=|x|
y=½|x|
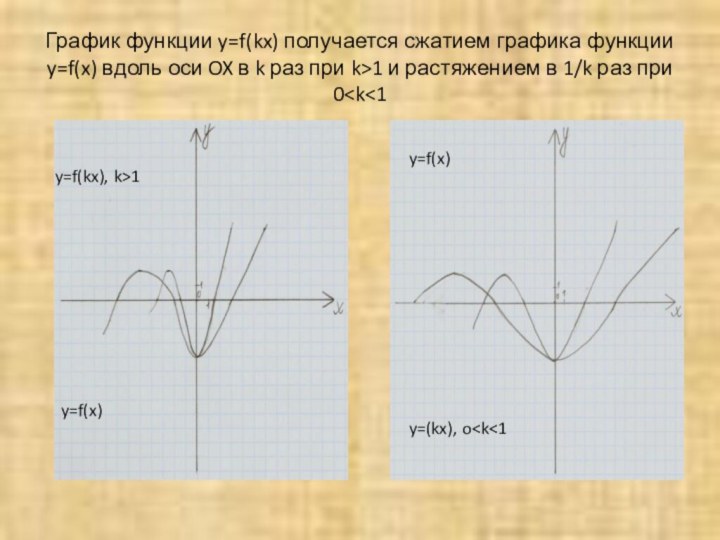
Слайд 9 График функции y=f(kx) получается сжатием графика функции y=f(x)
вдоль оси OX в k раз при k>1 и
растяжением в 1/k раз при 0y=f(x)
y=(kx), o y=f(kx), k>1 y=f(x)
Слайд 10 График функции y=-f(x) получается симметричным отображением графика функции
y=f(x) относительно оси OX.
y=3x2
y=3x+2
y=2x²8x+6
y=2x²+8x6
Слайд 11 График функции y=f(-x) получается симметричным отображением графика функции
y=f(x) относительно оси OY.
y=3x2
y=3x2
y=корень из -2x+3
y=корень из 2x+3
Слайд 12
Построение графиков, содержащих несколько преобразований
y=2(х-3)²+4
y=x²→y=(x3)²→y=2(x3)²→y=2(x3)²→y=2(x3)²+4
y=2+3/(х-4)
y=3/х →y=3/(x4)→y=2+3/(x4)
Слайд 13 График функции y=If(x)I получается из графика функции y=f(x)
следующим образом: часть графика, расположенная ниже оси OX,симметрично отображается
относительно этой оси; остальная его часть остаётся без измененийy=|3x5|
y=|3/x2|
Слайд 14 График функции y=f(|x|) получается из графика функции y=f(x)
следующим образом :часть графика, расположенная в области x≥0,остается без
изменений, и эта же часть графика симметрично отображается относительно оси OYy=x²4|x|+1
y=5|x|3
y=(x2)²3
y=5x-3
Слайд 16 График зависимости |y|=f(x) получается из графика y=f(x), если
все точки, для которых f(x)≥0 сохраняются и они же
переносятся симметрично относительно оси абсцисс|y|=3x - 5
y=3x - 5