вынесем за скобки А:
(А ^ В) v (А
^ ¬В) = А ^ (В v ¬В).По закону исключенного третьего В v ¬В = 1, следовательно
А ^ (В v ¬B) = А ^ 1 = А.
(А ^ В) v (A ^ ¬В)
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







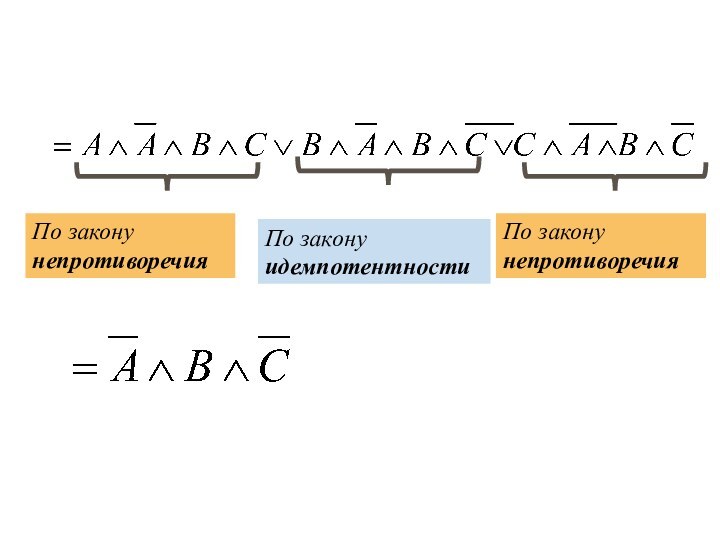

(А ^ В) v (A ^ ¬В)
правило де Моргана