Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к научной работе по математике Софизмы (8 класс)

Содержание

В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.  И. Ньютон
Софизмы в математикеАвторы: Шеметова Анастасия, Глазунова Екатерина, ученицы 8Б класса МБОУ В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.  И. Ньютон Актуальность Каждый человек хоть раз в жизни слышал фразу: «Дважды два равно пяти» Цель:Исследование типичных ошибок, которые возникают у учащихся в процессе изучения математики, их Гипотеза исследования Если в процессе обучения математике целенаправленно и систематически организовывать Софизм - преднамеренная ошибка, совершаемая с целью запутать противника и выдать ложное Софисты Мудрецы особого рода. Этих мудрецов истина не интересовала. Они были, Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо Математические софизмыАрифметические софизмыАлгебраические софизмыГеометрические софизмыЛогические софизмыМатематический софизм - удивительное утверждение, в доказательстве Типичные софизмы в математике : запрещенные действия; пренебрежение условиями теорем, формул Арифметические софизмы Пример: « Дважды два - пять!» Ошибка: Распределительный закон умножнения Алгебраические софизмы Пример : Упростить выражение.Ошибка: Неверное извлечение квадратного корня из квадрата Геометрические софизмыПример: «Катет равен гипотенузе».∟С=90, ВД - биссектриса ∟ СВА, СК=КА, ОК Ошибка: Выводы и вычисления по неверно построенным чертежам. Логические софизмыПример:«Полупустое или полуполное» Полупустое есть то же, что и полуполное. Если равны Примеры рассмотренных софизмов:«Пять равно шести».«Уравнение х-а=0 не имеет корней».«Один метр не равен Источники софизмовМногие слова имеют несколько смыслов.Неправильное ударение.Пренебрежение условиями теорем, формул и правил; «Софизмы из наших школьных тетрадей» Цель практической работы: составить сборник софизмов, на основе Алгебраические софизмы Пример № 1 Решить уравнение. Ошибка: Отклонение от алгоритма может привести Пример № 2 «Сокращение дробей». Пример № 3 «Выполнить действие». -10 Пример № 4 «Свойства степени».Ошибка:Правило: Геометрический софизм Пример № 5 «Неравенство треугольника».1х3х2хР=61х+2х+3х=66х=6х=12х=2 Заключение В процессе обучения математики обнаружение и анализирование ошибки, заключенной в софизме, Литература«Софисты» под редакцией Б.С. Чернышева«Софизмы. Алгебра. Геометрия. Тригонометрия» под редакцией Т.Н. Михеевой
Слайды презентации

Слайд 2 В математических вопросах нельзя
пренебрегать даже самыми
мелкими

В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.  И. Ньютон

ошибками.  И. Ньютон

Слайд 3 Актуальность
Каждый человек хоть раз в жизни слышал фразу:

Актуальность Каждый человек хоть раз в жизни слышал фразу: «Дважды два равно


«Дважды два равно пяти»
«Два равно трем».
Что они

обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь вымысел? Чтобы ответить на эти и подобные им вопросы, мы в своей работе рассматриваем математические софизмы.

Слайд 4 Цель:
Исследование типичных ошибок, которые возникают у учащихся в

Цель:Исследование типичных ошибок, которые возникают у учащихся в процессе изучения математики,

процессе изучения математики, их причин и способов предупреждения.
Задачи:
изучить понятие

софизма и историю его возникновения;
рассмотреть виды софизмов и дать классификацию их ошибок;
составить сборник задач на софизмы по различным разделам математики для 6 -9 классов.

Слайд 5 Гипотеза исследования
Если в процессе обучения

Гипотеза исследования Если в процессе обучения математике целенаправленно и систематически

математике целенаправленно и систематически организовывать работу учащихся над типичными

ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

 
 
 

Слайд 6 Софизм - преднамеренная ошибка, совершаемая с целью запутать

Софизм - преднамеренная ошибка, совершаемая с целью запутать противника и выдать

противника и выдать ложное суждение за истинное. Софистика – направление

философии, которое возникло в V-IV вв. до н.э. в Греции и стало очень популярным в Афинах.

Слайд 7 Софисты
Мудрецы особого рода. Этих мудрецов истина

Софисты Мудрецы особого рода. Этих мудрецов истина не интересовала. Они были,

не интересовала. Они были, как правило, платными «учителями мудрости».

Протагор
490

г. до н.э.-411 г. до н.э.

Сократ
469 г. до н.э.-
399 г. до н.э.

Аристотель
384 г. до н.э.-322 г. до н.э.

Слайд 8 Убедительность на первый взгляд многих софизмов, их «логичность»

Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с

обычно связана с хорошо замаскированной ошибкой, с использованием, например,

«неразрешённых» или даже «запрещённых» правил или действий.

Слайд 9 Математические софизмы
Арифметические софизмы
Алгебраические софизмы
Геометрические софизмы
Логические софизмы
Математический софизм -

Математические софизмыАрифметические софизмыАлгебраические софизмыГеометрические софизмыЛогические софизмыМатематический софизм - удивительное утверждение, в

удивительное утверждение, в доказательстве которого кроются незаметные, а подчас

и довольно тонкие ошибки.

Слайд 10 Типичные софизмы в математике :
запрещенные действия;
пренебрежение

Типичные софизмы в математике : запрещенные действия; пренебрежение условиями теорем, формул

условиями теорем, формул и правил;
ошибочный чертеж;
опора на ошибочные умозаключения.

Слайд 11 Арифметические софизмы
Пример: « Дважды два - пять!»

Арифметические софизмы Пример: « Дважды два - пять!» Ошибка: Распределительный закон










Ошибка: Распределительный закон умножнения применяется только для сложения и

вычитания.
ав + ас = а(в + с).


Слайд 12 Алгебраические софизмы
Пример : Упростить выражение.


Ошибка: Неверное извлечение

Алгебраические софизмы Пример : Упростить выражение.Ошибка: Неверное извлечение квадратного корня из

квадратного корня из квадрата выражения

= х
2 - < 0

= = = 2- = - 2


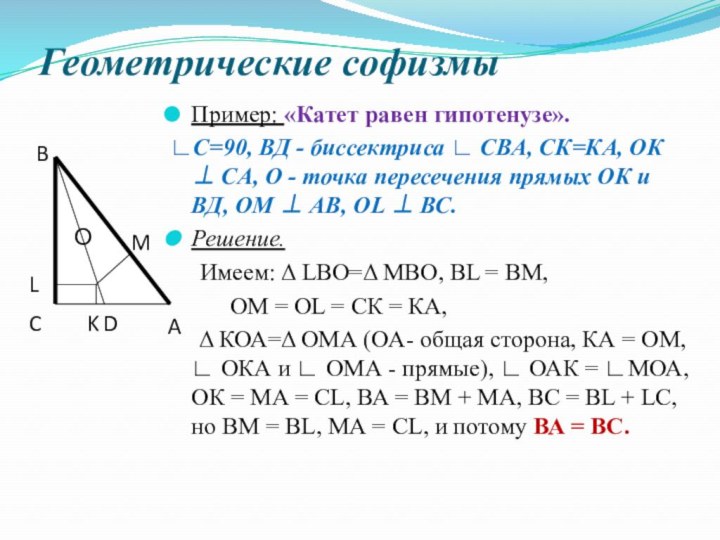
Слайд 13 Геометрические софизмы
Пример: «Катет равен гипотенузе».
∟С=90, ВД - биссектриса

Геометрические софизмыПример: «Катет равен гипотенузе».∟С=90, ВД - биссектриса ∟ СВА, СК=КА,

∟ СВА, СК=КА, ОК  СА, О - точка

пересечения прямых ОК и ВД, ОМ  АВ, ОL  ВС.
Решение.
Имеем:  LВО= МВО, ВL = ВМ,
ОМ = ОL = СК = КА,
 КОА= ОМА (ОA- общая сторона, КА = ОМ, ∟ ОКА и ∟ ОМА - прямые), ∟ ОАК = ∟МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС.

О

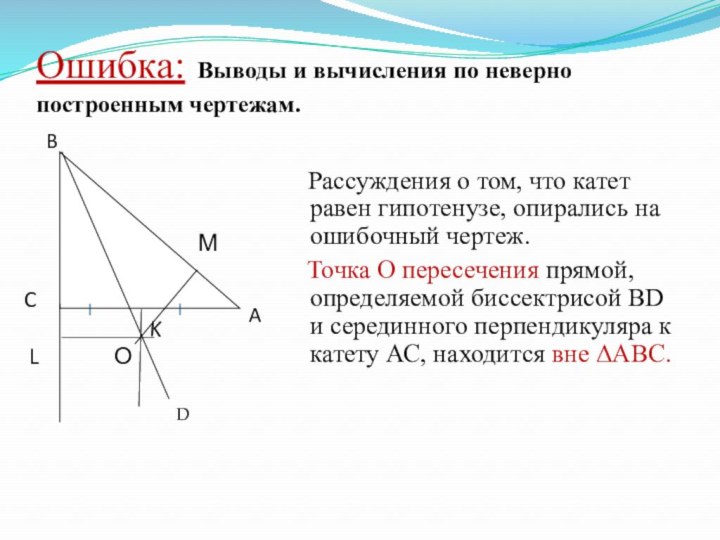
Слайд 14 Ошибка: Выводы и вычисления по неверно построенным

Ошибка: Выводы и вычисления по неверно построенным чертежам. Рассуждения

чертежам.
Рассуждения о том, что катет равен гипотенузе,

опирались на ошибочный чертеж.
Точка О пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне АВС.

Слайд 15 Логические софизмы
Пример:«Полупустое или полуполное»
Полупустое есть то же, что

Логические софизмыПример:«Полупустое или полуполное» Полупустое есть то же, что и полуполное. Если

и полуполное. Если равны половины, значит, равны и целые.

Следовательно, пустое есть то же, что и полное
Ошибка:
Полупустое не является половиной чего либо пустого, а является чем либо наполовину наполненным.

Слайд 16 Примеры рассмотренных софизмов:
«Пять равно шести».
«Уравнение х-а=0 не имеет

Примеры рассмотренных софизмов:«Пять равно шести».«Уравнение х-а=0 не имеет корней».«Один метр не

корней».
«Один метр не равен ста сантиметрам».
«Один рубль не равен

ста копейкам».
«Два неодинаковых натуральных числа равны между собой».
«Если А больше В, то А всегда больше, чем 2В».



Слайд 17 Источники софизмов

Многие слова имеют несколько смыслов.
Неправильное ударение.
Пренебрежение условиями

Источники софизмовМногие слова имеют несколько смыслов.Неправильное ударение.Пренебрежение условиями теорем, формул и

теорем, формул и правил; ошибочный чертеж.
Опора на ошибочные

умозаключения.





Слайд 18 «Софизмы из наших школьных тетрадей»
Цель практической работы: составить

«Софизмы из наших школьных тетрадей» Цель практической работы: составить сборник софизмов, на

сборник софизмов, на основе анализа контрольных работ и типичных

ошибок.

 Ошибка – вещь необходимая и полезная!

Слайд 19 Алгебраические софизмы Пример № 1 Решить уравнение.
Ошибка: Отклонение от

Алгебраические софизмы Пример № 1 Решить уравнение. Ошибка: Отклонение от алгоритма может

алгоритма может привести к приобретению посторонних корней данного уравнения.

Слайд 20 Пример № 2
«Сокращение дробей».

Пример № 2 «Сокращение дробей».


Ошибка : нарушение правил сокращения дробей.




Слайд 21 Пример № 3 «Выполнить действие».

Пример № 3 «Выполнить действие». -10 *

-10 *

=11-10 * = =

= = 0,8
Ошибка: Неправильный порядок действий:


3 1 2

Слайд 22 Пример № 4 «Свойства степени».
Ошибка:
Правило:

Пример № 4 «Свойства степени».Ошибка:Правило:

Слайд 23 Геометрический софизм Пример № 5 «Неравенство треугольника».
1х
3х
2х
Р=6
1х+2х+3х=6
6х=6
х=1
2х=2

Геометрический софизм Пример № 5 «Неравенство треугольника».1х3х2хР=61х+2х+3х=66х=6х=12х=2

Слайд 24 Заключение
В процессе обучения математики обнаружение и анализирование

Заключение В процессе обучения математики обнаружение и анализирование ошибки, заключенной в

ошибки, заключенной в софизме, оказываются более важными, чем просто

разбор решений «безошибочных» задач.
  • Имя файла: prezentatsiya-k-nauchnoy-rabote-po-matematike-sofizmy-8-klass.pptx
  • Количество просмотров: 191
  • Количество скачиваний: 1
- Предыдущая Презентация Учусь быть гражданином!
Следующая - Презентация Дети и дорога

Похожие презентации

Решение задач с помощью рациональных уравнений Решение задач с помощью рациональных уравнений 159
Уравнения Уравнения 140
Презентация Своя игра к уроку алгебры (9 класс). Систематизация знаний по теме Квадратичная функция Презентация Своя игра к уроку алгебры (9 класс). Систематизация знаний по теме Квадратичная функция 202
Свойства функций Свойства функций 152
Презентация по математике на тему Исследование функций с применением производной (11 класс) Презентация по математике на тему Исследование функций с применением производной (11 класс) 174
Решение задач с помощью пропорций Решение задач с помощью пропорций 185
Интегрирование рациональных функций Интегрирование рациональных функций 156
Задачи на готовых чертежах Свойства равнобедренного треугольника Задачи на готовых чертежах Свойства равнобедренного треугольника 236
Построение диаграмм и графиков Построение диаграмм и графиков 138
Свойства степеней в преобразовании выражений Свойства степеней в преобразовании выражений 186
Презентация по алгебре действия с многочленом Презентация по алгебре действия с многочленом 146
Логические операции Логические операции 192
Старая сказка на новый лад Старая сказка на новый лад 174
Презентация Решение неравенств методом интервалов Презентация Решение неравенств методом интервалов 92
Дидактическая игра на тему ВПР Запись чисел с использованием разных систем измерения Дидактическая игра на тему ВПР Запись чисел с использованием разных систем измерения 193
Презентация по алгебре для 8 класса Множества Презентация по алгебре для 8 класса Множества 166
Презентация к уроку по алгебре на тему Применение производной к исследованию функции (11 класс) Презентация к уроку по алгебре на тему Применение производной к исследованию функции (11 класс) 154
Презентация по математике на тему Формулы приведения Презентация по математике на тему Формулы приведения 167
Пересечение и объединение множеств (8 класс) Пересечение и объединение множеств (8 класс) 192
Презентация по математике Делимость чисел,11 класс Презентация по математике Делимость чисел,11 класс 188
Презентация по алгебре Показательная функция Презентация по алгебре Показательная функция 175
Приближенные значения логарифма и решение прикладных задач Приближенные значения логарифма и решение прикладных задач 196
Презентация по математике Числа Фибоначчи Презентация по математике Числа Фибоначчи 177
Решение задач на отыскание экстремумов Решение задач на отыскание экстремумов 165
Презентация по математике на тему: Квадратные уравнения Презентация по математике на тему: Квадратные уравнения 170
Презентация к уроку алгебры в 7 классе по теме Умножение и деление степеней Презентация к уроку алгебры в 7 классе по теме Умножение и деление степеней 185
11 сынып логарифмдік теңдеу 11 сынып логарифмдік теңдеу 291
Умножение двузначного числа на однозначное Умножение двузначного числа на однозначное 150
Решение систем двух линейных уравнений с двумя переменными различными способами Решение систем двух линейных уравнений с двумя переменными различными способами 148
Презентация по математике на тему Многочлены от одной переменной (10, 11 классы) Презентация по математике на тему Многочлены от одной переменной (10, 11 классы) 267