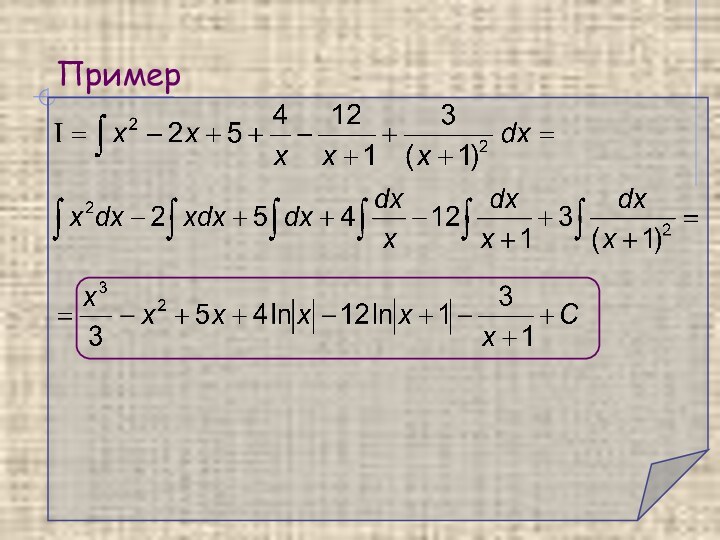функция, равная отношению двух многочленов:
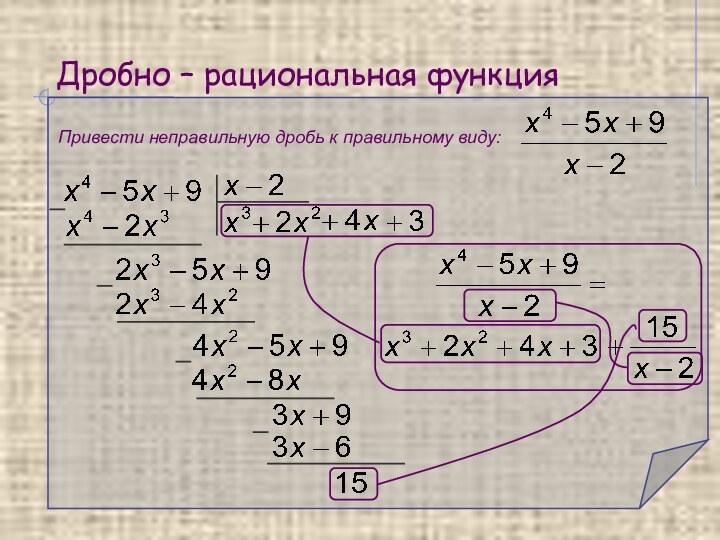
Рациональная дробь называется правильной, если
степень числителя меньше степени знаменателя, то есть m < n , в противном случае дробь называется неправильной. Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби: