- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Теорема Пифагора
Содержание
- 3. Цель исследования:Узнать о жизни Пифагора; о
- 5. Не делай никогда того, что тебе не знакомо, но научись всему, что следует знать.
- 6. Пифагор Самосский (570—490
- 7. Биография пифагораОбучение длиной в 30 летПо
- 8. ПифагорейцыИстория теоремы Пифагора- связана с развитием созданной
- 9. История теоремы ПифагораНасчитывает несколько тысячелетий. Утверждение,
- 10. Раньше теорема Пифагора называлась теоремой
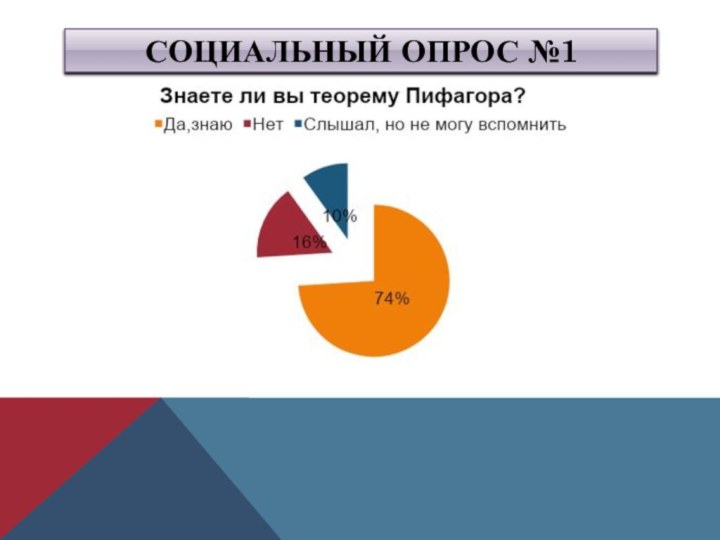
- 11. Социальный опрос №1
- 12. Социальный опрос №2
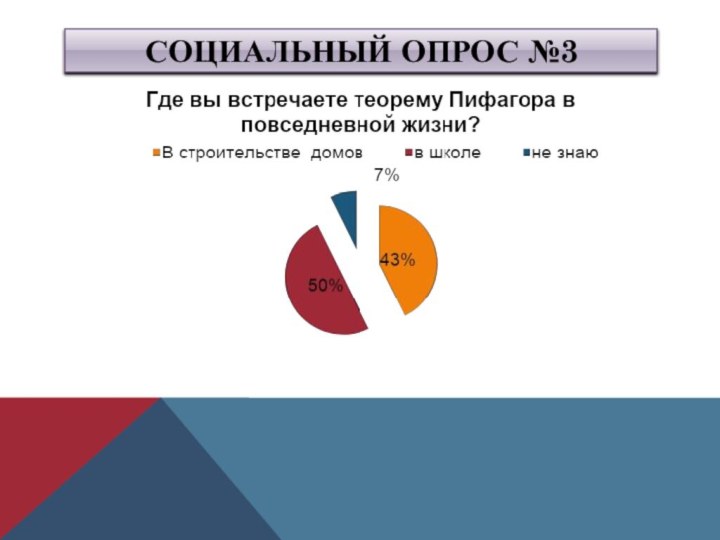
- 13. Социальный опрос №3
- 14. Социальный опрос №4
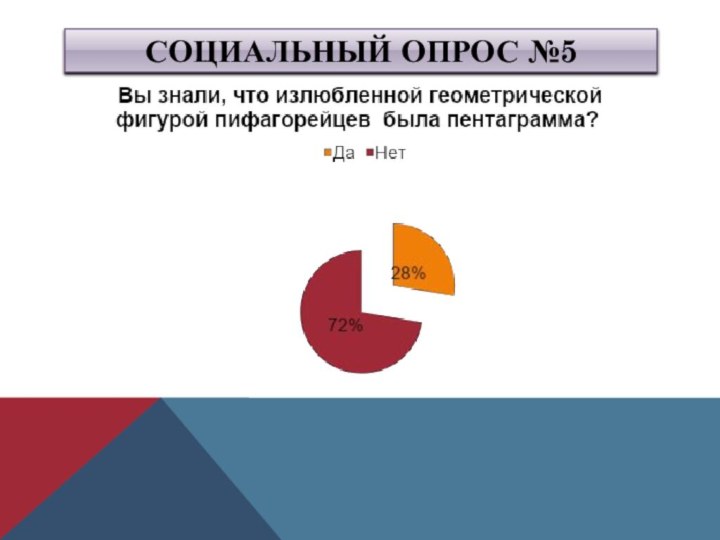
- 15. Социальный опрос №5
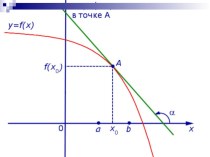
- 17. Геометрическая формулировка ТЕОРЕМЫ ПИФАГОРАВ прямоугольном треугольнике площадь
- 18. Алгебраическая Формулировки теоремы Пифагора В прямоугольном треугольнике
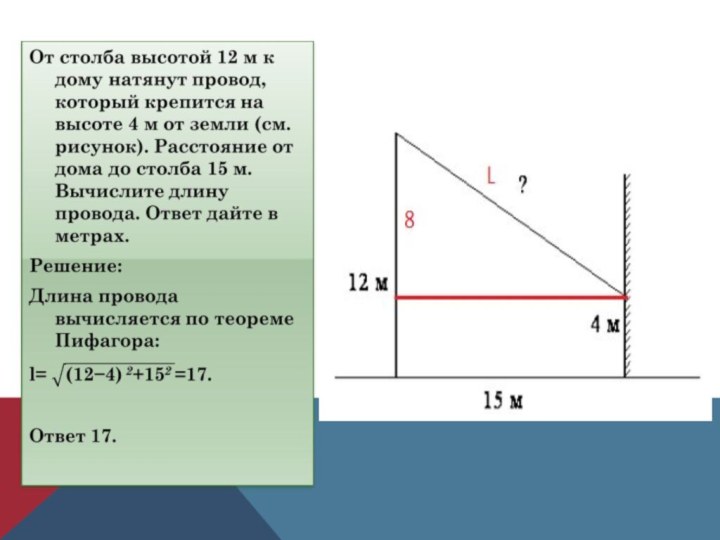
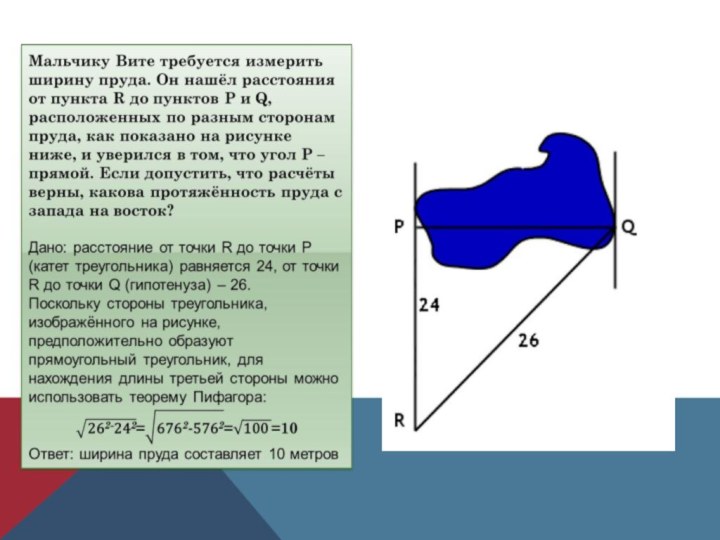
- 19. Решение прикладных задач с теоремой Пифагора
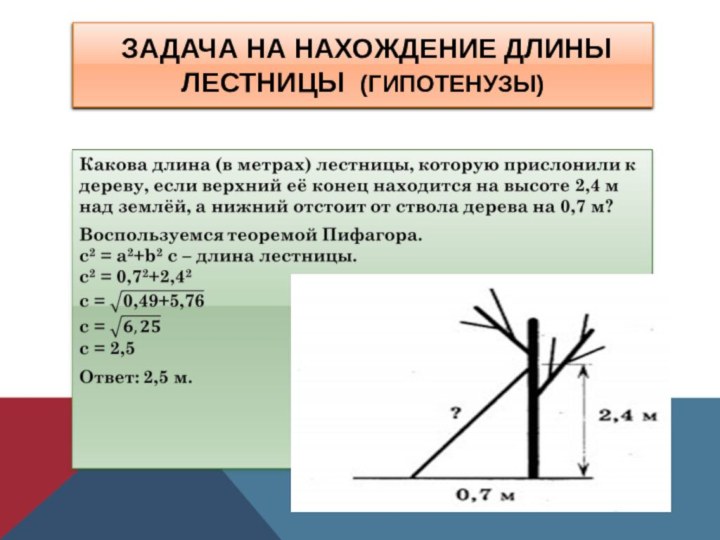
- 20. Задача на нахождение длины лестницы (гипотенузы)
- 21. Задача на нахождение неизвестного катета
- 22. Задача на нахождение радиуса описанной окружности около прямоугольного треугольника
- 23. Исторические задачиИз учебника Леонтия Магницкого. Случися
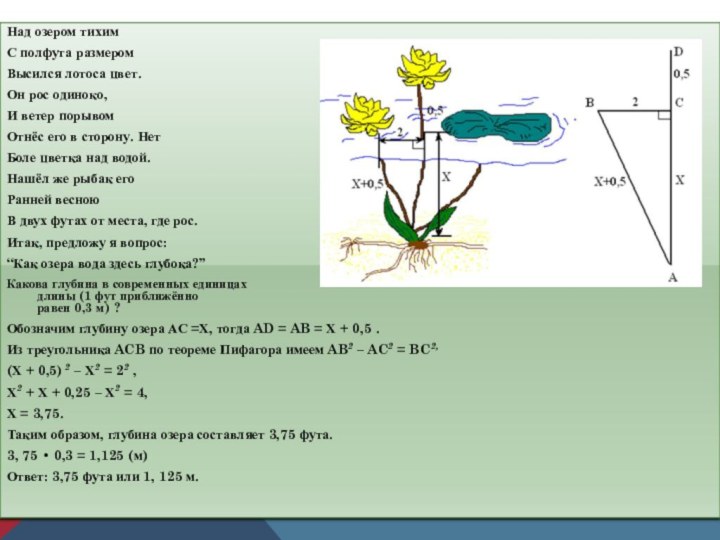
- 24. Над озером тихимС полфута размеромВысился лотоса цвет.Он
- 25. Применение теоремы ПифагораАвиацияСтроительство1)Крыша2)Молниеотвод3)КораблестроениеМобильная связьФизикаЛитератураМузыка
- 28. строительство крышШирина здания - 5,5 м.
- 29. кораблестроение Для крепления мачты нужно
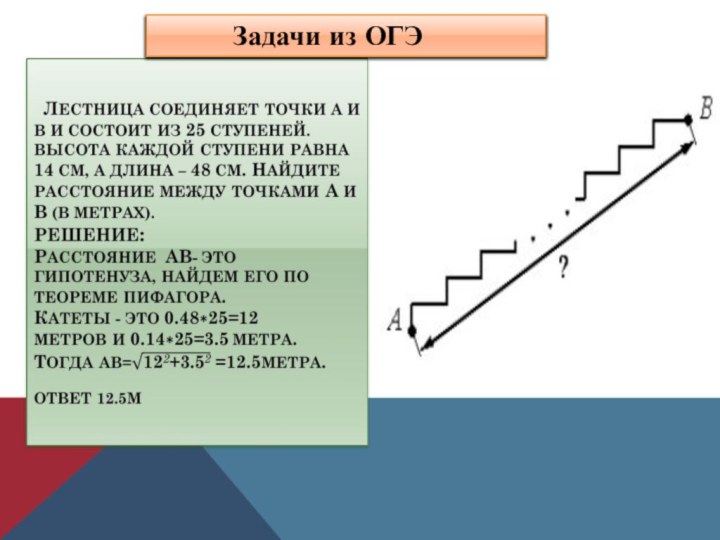
- 32. Задачи из ОГЭ
- 35. стихи про Пифагора и его
- 37. Необходимые ресурсы1.
- 39. Скачать презентацию
- 40. Похожие презентации
Цель исследования:Узнать о жизни Пифагора; о возникновении самой теоремы; её применение в повседневной жизни.Предмет исследования:Теорема Пифагора и её применение к решению задач прикладного характера





























Слайд 3
Цель исследования:
Узнать о жизни Пифагора; о возникновении
самой теоремы; её применение в повседневной жизни.
и её применение к решению задач прикладного характераСлайд 4
ЗАДАЧИ:
Рассмотреть историю возникновения теоремы Пифагора
Выявить, в каких областях применяется
теорема ПифагораИзучить методы решения задач с применением теоремы Пифагора
Составить задачи прикладного характера на применение теоремы Пифагора
Слайд 6
Пифагор Самосский (570—490 гг.
до н. э.) — древнегреческий философ, математик, мистик, создатель религиозно-философской школы пифагорейцев.
Кто же это такой?
Слайд 7
Биография пифагора
Обучение длиной в 30 лет
По одной
из версий, будучи пытливым юношей, Пифагор покинул родину. Он
отправился искать знаний в Египет, где пробыл, согласно разным источникам, от 11 до 22 лет, а затем попал в плен и был отправлен в Вавилон. Пифагор смог извлечь пользу из своего положения. В течение 12 лет он изучал математику и геометрию в древнем государстве. На Самос Пифагор вернулся только в 56 лет. Здесь в то время правил тиран Поликрат. Пифагор не смог принять такую политическую систему и вскоре отправился на юг Италии, где располагалась греческая колония Кротон.
Слайд 8
Пифагорейцы
История теоремы Пифагора- связана с развитием созданной греческим
философом школы. Это религиозно-этическое братство проповедовало соблюдение особого образа
жизни, изучало арифметику, геометрию и астрономию, занималось исследованием философской и мистической стороны чисел.Все открытия учеников греческого математика приписывались ему. Однако история возникновения теоремы Пифагора связывается древними биографами только с самим философом. Предполагается, что он передал грекам знания, полученные в Вавилоне и Египте. Есть также версия, что он действительно открыл теорему о соотношениях катетов и гипотенузы, не зная о достижениях других народов
.
Слайд 9
История теоремы Пифагора
Насчитывает несколько тысячелетий. Утверждение, гласящее,
что квадрат гипотенузы равен сумме квадратов катетов, было известно
еще задолго до рождения греческого математика. Однако теорема Пифагора, история создания и доказательства ее связываются для большинства именно с этим ученым. Согласно некоторым источникам, причиной тому послужило первое доказательство теоремы, которое было приведено Пифагором. Однако часть исследователей опровергает этот факт.Бюст Пифагора в Капитолийском музее в Риме
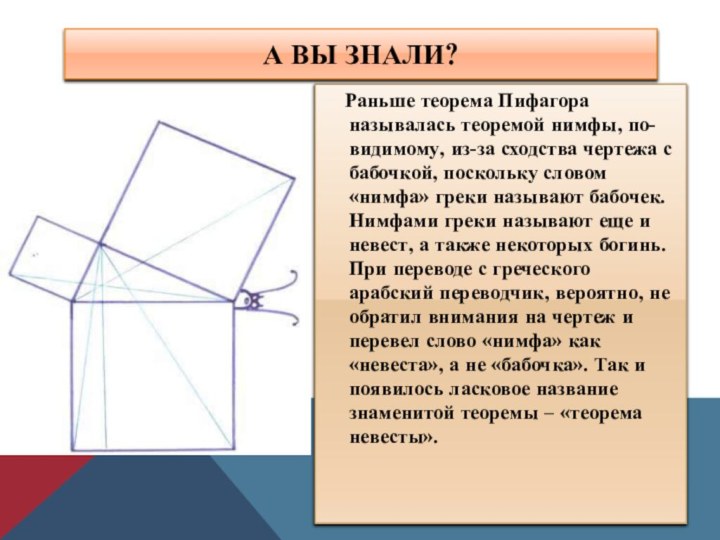
Слайд 10 Раньше теорема Пифагора называлась теоремой нимфы,
по-видимому, из-за сходства чертежа с бабочкой, поскольку словом «нимфа»
греки называют бабочек. Нимфами греки называют еще и невест, а также некоторых богинь. При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» как «невеста», а не «бабочка». Так и появилось ласковое название знаменитой теоремы – «теорема невесты».А вы знали?
Слайд 17
Геометрическая формулировка
ТЕОРЕМЫ ПИФАГОРА
В прямоугольном треугольнике площадь квадрата, построенного
на гипотенузе равна сумме площадей квадратов, построенных на катетах.
Слайд 18
Алгебраическая Формулировки теоремы Пифагора
В прямоугольном треугольнике квадрат
длины гипотенузы равен сумме квадратов длин катетов.
c – длина
гипотенузы, a, b – длины катетов
Слайд 23
Исторические задачи
Из учебника Леонтия Магницкого. Случися некоему
человеку к стене лествицу прибрати, стены же тоя высота
есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать .Решение:
x2+1172=1252
x2=442
x=44
Ответ: 44 стопы
Слайд 24
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос
одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка
над водой.Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ?
Обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2,
(Х + 0,5) 2 – Х2 = 22 ,
Х2 + Х + 0,25 – Х2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
Слайд 25
Применение теоремы Пифагора
Авиация
Строительство
1)Крыша
2)Молниеотвод
3)Кораблестроение
Мобильная связь
Физика
Литература
Музыка
Слайд 26
Авиация
С аэродрома вылетели одновременно два
самолёта: один - на запад, другой - на юг. Через два часа расстояние между ними было 2000 км. Найдите скорости самолётов, если скорость одного составляла 75% скорости другого.Решение:
По теореме Пифагора:
4x2+(0,75x*2)2=20002
6,25x2=20002
2,5x=2000
x=800
0,75x=0,75*800=600.
Ответ: 800 км/ч.; 600 км/ч
Слайд 27
Молниеотвод
Молниеотвод защищает от молнии все предметы, расстояние
до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.Решение:
По теореме Пифагора h2 ≥ a2+b2, значит h ≥ (a2+b2)½.
Ответ: h ≥ (a2+b2)½
Слайд 28
строительство крыш
Ширина здания - 5,5 м. Высота
– 3м. Какой длины будут стропила?
Решение: высота крыши (первый
катет) – 3 метра.Длина второго катета = 5,5:2 = 2,75 м.
По теореме Пифагора находим гипотенузу (стропила):
х2= 2,752 + 32 ≈ 16,5625
х ≈ 4,07
Ответ: длина стропил – 4,07 метров.
Слайд 29
кораблестроение
Для крепления мачты нужно установить
4 троса, один конец каждого троса должен крепиться на
высоте 12 метров, другой-на земле на расстоянии 5 метров от мачты. Хватит ли 50 м троса для крепления мачты.Трос - гипотенуза, а катеты – мачта и земля
Мачта = 12м; Земля = 5 м.
Гипотенуза равна: c2 = a2+ b2 = 122 + 52 = 144 + 25 = 169 c = 13 м - это длина одного троса. Длина 4 тросов 13*4 = 52 м.
Т.к. 52>50, значит 50 м троса не хватит. Ответ: 50 м не хватит.
Слайд 30
Физика
Найдите равнодействующую трёх
сил по 200 Н каждая, если угол между первой и второй силами и между второй и третьей силами равен 60°Решение:
Модуль суммы первой пары сил равен:
F1+22=F12+F22+2*F1*F2 cos α
где α - угол между векторами F1 и F2, т.е. F1+2=200 √3 Н. Как ясно из соображений симметрии вектор F1+2 направлен по биссектрисе угла α, поэтому угол между ним и третьей силой равен:
β=60°+60°/2=90°.
Теперь найдём равнодействующую трёх сил:
R2=(F3+F1+2 )
R=400 Н.
Ответ: R=400 Н.
Слайд 31
Мобильная связь
СВЯЗЬ Какую наибольшую высоту должна иметь антенна мобильного
оператора, чтобы передачу можно было принимать в радиусе R=50 км. Радиус Земли равен 6380 км. Из треугольника ОВС по теореме Пифагора получаем, что сторона ОВ=6380,35км. Из этого следует, что АВ=0,35 км или 350 м
Слайд 35
стихи про Пифагора
и его теорему
Если дан
нам треугольник
И притом с
прямым углом,То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
Слайд 36
Вывод
Появление
задач прикладного характера обусловлено практической деятельностью человекаТеорема Пифагора применяется в различных областях
Первые прикладные задачи с использованием теоремы Пифагора были решены в глубокой древности
Задачи прикладного характера интересны ученикам школы
Результаты исследования могут быть полезны на уроках математики и на внеклассных занятиях
Слайд 37
Необходимые ресурсы
1. Техническое
оснащение: фотоаппарат, компьютер, интернет.
2. Программное обеспечение: прикладной пакет Microsoft
Word для создания текстовых фрагментов, прикладной пакет Microsoft Power Point для создания презентаций.3. Школьные ресурсы информации.
Слайд 38 Продолжите
фразу
Сегодня на уроке я узнал..
Для меня стало неожиданным..
Мне удалось..
Мне
хочется попробовать..Настроение после нашей работы..