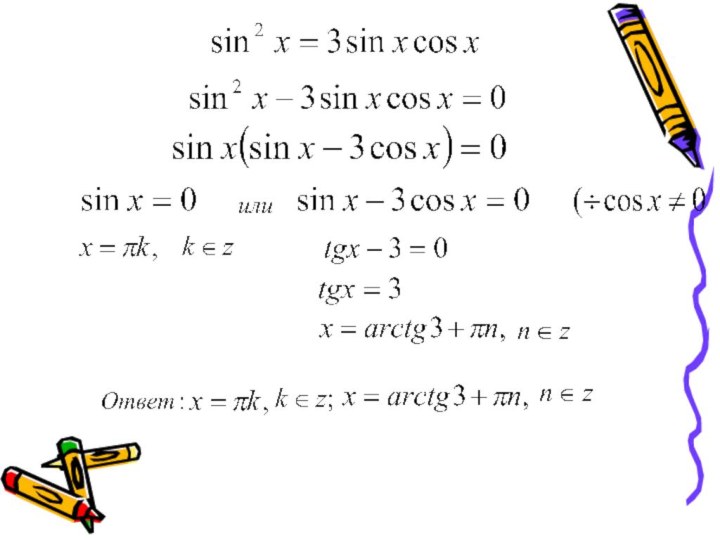простейших тригонометрических уравнений.
Уметь:
Вычислять значения тригонометрических функций.
Вычислять значения обратных тригонометрических
функций.Решать простейшие тригонометрические уравнения.
Выполнять тождественные преобразования выражений.