Слайд 2
Решение неравенств
§1.Решение неравенств, содержащих квадратный трехчлен:
§2.Решение целых

рациональных неравенств
§3.Решение дробно-рациональных неравенств
§4.Неравенства, содержащие знак модуля.
§5.Иррациональные неравенства.
§6.Уравнения и
неравенства с параметрами.
6.1.Графический метод решения задач с параметрами.
§7.Решение неравенств методом интервала
§8.Решение неравенств с помощью параболы
Решение квадратных уравнений графическим способом
Виды квадратичной функции
§1.Функция y=ax2
§2. Квадратичная функция
Преобразование графиков функции y=a(x-m)2+n
§1. Растяжение
§2. Параллельный перенос по оси Ox
§3. Параллельный перенос по оси Oy
Сечение конуса
Построение параболы по трем точкам
Заключение
Приложения
Список использованной литературы
Содержание:
Цель
Задачи
Проблемы исследования
Квадратное уравнение
§1.Определение
§2.Решение неполных квадратных уравнений
§3.Формулы корней квадратного уравнения
§4.Алгоритм решения квадратных уравнений
§5.Алгорит устного решения квадратных уравнений
Теорема Виета
§1. Следствия из теоремы Виета
Неравенства
§1.свойтсва неравенств
Слайд 3
Цель:
1. Исследовать квадратный трехчлен и осуществить его полный
анализ.
2. Научиться применять его на практике.
3. Разработать свое методическое
пособие.
Слайд 4
Задачи:
1. Произвести анализ учебно-методической литературы.
2. Произвести анализ различных
способов решения квадратного трехчлена.
3. Изучить историю развития квадратного трехчлена.
Слайд 5
Проблемы исследования:
1. Заключается в выделении способов решения квадратного
трехчлена.
Объект исследования.
Организация
применения различных способов решения квадратного
трехчлена при изучении математики в школе.
Предмет исследования квадратный трехчлен.
Слайд 6
Квадратное уравнение
Квадратным уравнением называют уравнение вида ах²+bх+с=0, где
коэффициенты а, b, с - любые действительные числа, причём
а≠0. Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.
Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени.
определение
Слайд 7
Решение неполных квадратных уравнений
Неполное квадратное уравнение может иметь
два корня, один корень и ни одного корня.
Слайд 8
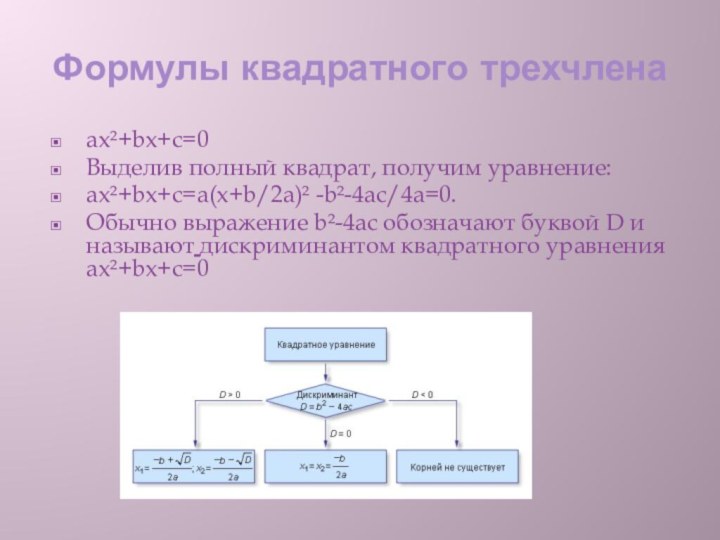
Формулы квадратного трехчлена
ах²+bх+с=0
Выделив полный квадрат, получим уравнение:
ах²+bх+с=а(х+b/2а)²
-b²-4ас/4а=0.
Обычно выражение b²-4ас обозначают буквой D и называют дискриминантом
квадратного уравнения ах²+bх+с=0
Слайд 9
Алгоритм решения квадратных уравнений
Вычислить Д квадратного уравнения по
формуле:
D=b²-4ас
Сделать вывод о знаке D и о количестве корней.
Если
D<0, то корней нет.
Если D=0, то один корень х=-b/2а
Если D>0 то, два корня х1=-b-√D/2а х2=-b+√D/2а
Записать ответ.
Слайд 10
Алгоритм устного решения квадратных уравнений
Приведенное квадратное уравнение имеет
вид
x2 + рх + q = 0
его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид
х1 · х2 = q,
х1 + х2 = - p
Отсюда можно сделать следующий вывод:
Если в уравнении последним знаком является «минус», то корни имеют разные знаки, причем знак меньше корня совпадает со знаком второго коэффициента в уравнении
Зная, что при сложении чисел с разными знаками их модули, вычитаются затем: для нахождения корней приведенного уравнения необходимо выполнить следующие действия:
найти такие множители числа q, чтобы их разность была равна числу р;
поставить пред меньшим из найденных чисел второй знак уравнения, другой корень будет иметь противоположный знак.
Слайд 11
Теорема Виета
Теорема: Сумма корней приведенного квадратного уравнения равна
второму коэффициенту с противоположным знаком, а произведение корней равно
свободному члену.
Доказательство:
Если х1 и х2 – корни, то их можно вычислять по формуле: х1,2=-р±√D/2
х1=-р-√D/2
+
х2=-р+√D/2
____________
-р+√D/2+-р-√D/2=-р+√D+-р-√D/2=-2р/2=-р
х1·х2=-р+√D/2·-р-√D/2=(-р+√D)(-р-√D)/4=р²-D/4=р²-(р²-4q)/4= р²- р²+4q/4=
=4q/4=q.
Слайд 12
Обратная теорема:
Если числа х1 и х2 таковы, что
х1+х2=-p, x1·x2=q, то эти числа корни приведенного уравнения х²+рх+q=0.
Доказательство:
По
условию х1+х2=-p, x1·x2=q, тогда можно составить квадратное уравнение х²+рх+q=0.
х²+рх+q=х²-(х1=х2)·х+х1·х2=х²-х1·х-х2·х+х1·х2=х(х-х1)-х2(х-х1)=(х-х1)(х-х2)
(х-х1)(х-х2)=0 <=> х-х1=0 х=х1
х-х2=0 х=х2
Слайд 13
Следствие из теоремы Виета
Следствие 1:
Для того, чтобы корни
квадратного трехчлена имели одинаковые знаки необходимо и достаточно выполнение
условий: чтобы D ≥ 0; чтобы х1·х2>0
Причем: 1) оба корня положительные если дополнительно выполняется равенство х1+х2>0
<=> b²-4ас≥0
с/а>0
-b/а>0
2) оба корня отрицательные если дополнительно выполняется равенство х1+х2<0
<=> b²-4ас≥0
с/а>0
-b/а<0
Следствие 2:
Для того, чтобы корни квадратного трехчлена имели различные знаки необходимо выполнения условий: чтобы D>0; чтобы х1·х2<0
<=> b²-4ас>0
с/а<0.
Слайд 14
неравенства
Пусть функции и
определены на некотором множестве . Поставим задачу:
найти множество , на котором значения одной из функций больше (меньше) значений другой из них, другими словами, найти все значения , для которых выполняется неравенство: > ( < ).
Множество называется множеством решений данного неравенства.
Решить неравенство – значит найти множество всех , для которых данное неравенство выполняется.
Слайд 15
Свойства неравенств
пусть
, тогда
и
пусть
, тогда
Слайд 16
Решение неравенств
Решение неравенств, содержащих квадратный трехчлен
Решение неравенств, содержащих
квадратный трехчлен:
Пусть - дискриминант квадратного трехчлена.
Слайд 17
§2.Решение целых рациональных неравенств
Если в неравенстве функции и
заданы целыми рациональными выражениями, то его называют целым рациональным
неравенством.
Если неравенство привести к равносильному и разложить левую часть на линейные множители, то такое неравенство можно решить методом интервалов.
Суть этого метода в следующем:
Перенести все слагаемые в левую часть и решить уравнение, приравняв выражение в левой части к нулю;
Найденные корни уравнения нанести на числовую ость. Эти корни разбивают числовую ось на промежутки, на каждом из которых выражение, стоящее в левой части, сохраняет знак;
Выбрать в каждом из промежутков какое-нибудь значение («пробную» точку) и определить знак выражения в этой точке;
Выбрать промежутки, в которых выражение имеет требуемый знак и записать ответ, взяв их объединения.
Слайд 18
§3.Решение дробно-рациональных неравенств
Дробно рациональные неравенства можно привести к
равносильному неравенству , тогда метод интервалов применим и для
решения дробно-рациональных неравенств.
Слайд 19
§4.Неравенства, содержащие знак модуля.
Одним из методов решения неравенств,
содержащих знак модуля, является метод промежутков, который был рассмотрен
при решении уравнений с модулем.
Разобъем числовую ось точками, в которых обращаются в нуль выражения, стоящие под знаком модуля.
Выбирая на этих промежутках контрольные точки, проверяем, удовлетворяется ли на них заданное неравенство или нет. Ответом к задаче служит объединение промежутков, где выполняется данное неравенство.
Слайд 20
§5.Иррациональные неравенства.
Рассмотрим решение иррациональных неравенств, т.е. неравенств, в
которых неизвестная содержится под знаком радикала. Простейшие из них
имеют вид:
или .
При рассмотрении этих неравенств будут применяться следующие утверждения:
1. Неравенство вида (при натуральном ) равносильно системе неравенств:
2. Неравенство вида равносильно совокупности двух систем неравенств:
и
Слайд 21
§6.Уравнения и неравенства с параметрами.
Иногда в уравнениях и
неравенствах некоторые коэффициенты или свободные члены заданы не конкретными
числовыми значениями, а обозначены буквами. Такие буквы называются параметрами. Предполагается, что эти параметры могут принимать любые значения.
Решить уравнение с параметрами означает следующее:
а) исследовать, при каких значениях параметров уравнение имеет корни и сколько их при различных значениях параметров;
б) найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.
Слайд 22
6.1.Графический метод решения задач с параметрами.
Слайд 23
Метод интервалов основан на методе полной индукции (перебор
всех вариантов) и на свойстве непрерывной функции сохранять знак
между значениями, в которых она обращается в 0 (интервалы знакопостоянства)
Решение неравенств.
Рассмотрим график многочлена.. Это непрерывная функция. Значение 0 она приобретает 3 раза, f(x) = 0 в точках x1, x2, x3, корнях многочлена.
В промежутках между ними она сохраняет знак.
Поскольку для решение неравенства f(x)>0 нас интересует только знак функции, перейдем от графика к координатной прямой.
f(x)>0 при x (x1; x2) и при x (x3; )
f(x)<0 при x ( - ; x1) и при х (x2; x3)
Синим и красным цветом выделены решения неравенств f(x)<0, а красным – f(x)>0
Для определения знака функции на интервале достаточно знать знак функции в одной из точек интервала знакопостоянства.
Этим методом удобно решать неравенства, левая часть которых разложена на множители, поскольку в них не представляет труда найти корни.
Слайд 24
§8.Решение неравенств с помощью параболы
Графиком квадратичной функции (квадратного
трехчлена) у = ах2 + bх + с является
парабола. Расположение параболы в зависимости от знаков коэффициента а и дискриминанта D приведено на рис.
Числа х1 и х2 на оси абсцисс — корни квадратного уравнения ах2 + bх + + с = 0; координаты вершины параболы (точки А) во всех случаях
точка пересечения параболы с осью ординат имеет координаты (0; с).
Слайд 25
Решение квадратных уравнений графическим способом
Квадратное
уравнение можно решать и графическим способом. Решим графически уравнение
ах2 + bx +с = 0. Оно равносильно уравнению ах2 = - (bx + c). Постоим графики функций y = ax2 и y = - bx - c в одной системе координат (рис. 1). В точках х1 и х2 значения обеих функций равна. Следовательно, х1 и х2 являются корнями уравнения ах2 = - (bx + c) и равносильного ему уравнения ах2 + bx +с = 0
Если парабола и прямая касаются. То квадратное уравнение имеет два равных корня.
Если же парабола и прямая не пересекаются и не касаются, то квадратное уравнение не имеет корней.
Уравнение ах2 + bx +с = 0 можно решить иначе, построив параболу y = ах2 + bx +с и найдя точки ее пересечения с осью Ох, если D≥0 (рис. 2)2
Слайд 26
Область определения этой функции - множество R действительных
чисел.
Придавая переменной х несколько значений из области определения функции
и вычисляя соответствующие значения у по формуле y = x2 , изображаем график функции.
График функции y = ax2 называется параболой.
Слайд 27
Свойства функции у =aх2.
1. Если х = 0,
то у = 0, т.е. парабола имеет с осями
координат общую точку (0;0) - начало координат.
2. Если х ≠ 0, то у > 0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.
3. Множеством значений функции у = aх2 является промежуток [0; + ∞).
4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = aх2 - четная).
5. На промежутке [0; + ∞) функция у = aх2 возрастает.
6. На промежутке (-∞; 0] функция у = aх2 убывает.
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.
Слайд 28
Квадратичной функцией называется функция, которую можно записать
формулой вида y = ax2 + bx + c,
где x – независимая переменная, a, b и c – некоторые числа, причем a≠0.
Свойства функции и вид ее графика определяются, в основном, значениями коэффициента a и дискриминанта .
Слайд 29
Преобразование графиков функции y=a(x-m)2+n
§1. Растяжение
Растяжение графика у =
x2 вдоль оси у в |а| раз (при |а|
< 1 — это сжатие в 1/|а| раз).
Если, а < 0, произвести, кроме того, зеркальное отражение графика относительно оси х
Результат: график функции у = ах2.
Слайд 30
§2. Параллельный перенос по оси Ox
Параллельный перенос
графика функции у = ах2 вдоль оси х на
|m| (вправо при
m > 0 и влево при т < 0).
Результат: график функции у = а(х - т)2.
Слайд 31
§3. Параллельный перенос по оси Oy
Параллельный перенос графика
функции вдоль оси у на |n| (вверх при
п > 0 и вниз при п < 0).
Результат: график функции у = а(х - т)2 + п.
Слайд 32
Сечение конуса
Парабола является одним из конических сечений
Точка
является точкой
экстремума и называется вершиной параболы. Если a > 0, то в этой точке достигается минимум функции, и
Если a < 0, то в этой точке достигается максимум функции, и
Слайд 33
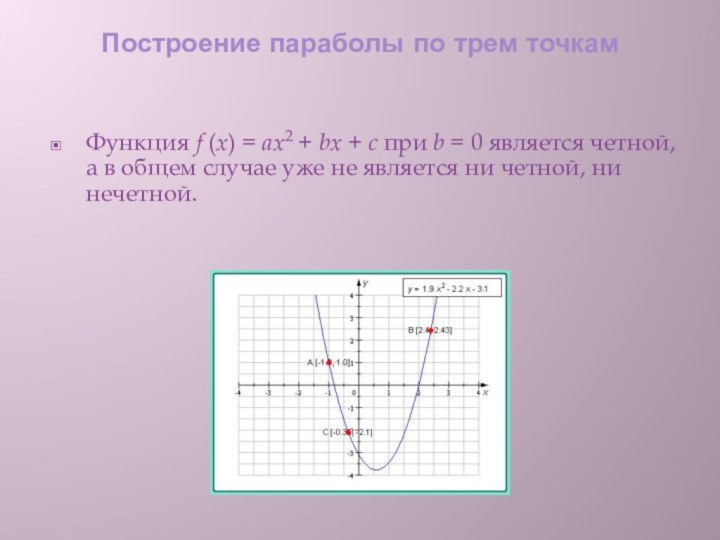
Построение параболы по трем точкам
Функция f (x) = ax2 + bx + c при b = 0
является четной, а в общем случае уже не является
ни четной, ни нечетной.
Слайд 34
Заключение
В результате выполнения исследования можно сделать следующие выводы:
Изучение
научно – методической литературы по теме выполненной работы показали,
что использование различных способов решения квадратных уравнений является важным звеном изучении математики, повышает интерес, развивает внимание и сообразительность.
Система использования различных способов решений уравнений на разных этапах урока является эффективным средством активизации учащихся, положительно влияет на повышение качества знаний, умений и навыков учащихся, развивает умственную деятельность.
Основным в решении квадратных уравнений является правильно выбрать рациональный способ решения и применить алгоритм решения
Работа над докладом способствует дальнейшему изучению решений уравнений.