- я забываю,
я
вижу – я запоминаю, я делаю – я понимаю»
Древняя китайская мудрость
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













a²
25x⁴y⁶
4c²
49
6ab²c
28xy
pq
2pq
26xy
12ab²c
c²
x⁴
(a+b)²
x²+5x+6
a²+a-30
m²+2mn+n²
a²+2ab+b²
(a+b)²
a²+2ab+b²
(m+n)²
m²+2mn+n²
(a-b)²
a²-2ab+b²
(m-n)²
m²-2mn+n²
a²-2ab+b²
m²-2mn+n²
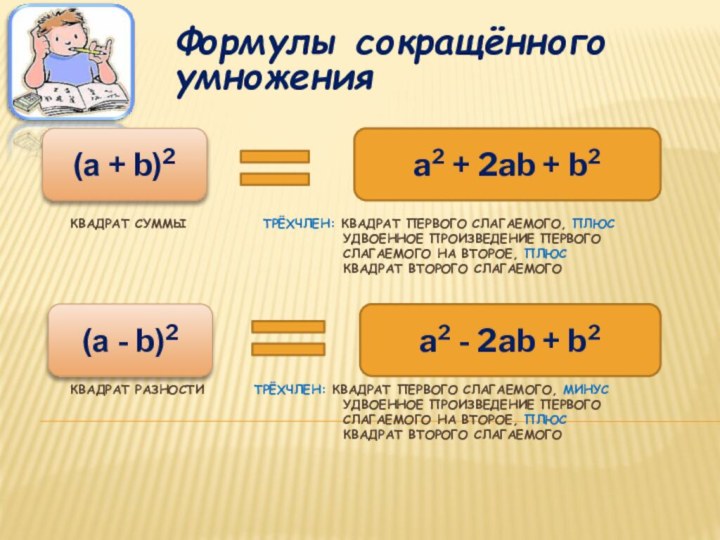
Формулы сокращённого умножения
(а + b)2
(а - b)2
a² + 2ab + b²
a² - 2ab + b²
2у
3х
3х
3х
2у
2у
х²+6ху+9у²
4c²-12cd+9d²
m²-2mn+4n²
16a²+8ab+b²
p²+2pq+9q²
x⁴+2x²y²+y⁴
20mn-5n²
a²b²-8ab+16
2a⁶+a³b³
X=4
X=7
X=6
(9m² - 2k)² = 81m⁴- 36 m²k + 4k²
(6a³ +5b)² = 36a⁶ + 60а³b +25b²
(3a³ – 4b²)² = 9a⁶ – 24a³b² + 16b⁴
(2m + 5k²)² = 4m² + 20mk² + 25k⁴
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
a²+2ab+b²
(a+b)²