Слайд 2
Метод интервалов
введение функции, отвечающей левой части неравенства, в
нашем случае – линейной функции y=a·x+b,
нахождение ее нулей, которые разбивают область
определения на промежутки,
определение знаков, которые имеют значения функции на этих промежутках, на основе которых делается вывод о решении линейного неравенства.
Слайд 3
Алгоритм решения a·x+b, ≥) при a≠0
1. Находятся нули
функции y=a·x+b, для чего решается линейное уравнениеa·x+b=0. Как известно, при a≠0 оно имеет
единственный корень, который обозначим x0.
2. Строится координатная прямая, и на ней изображается точка с координатой x0. Причем, если решается строгое неравенство (со знаком < или >), то эту точку делают выколотой (с пустым центром), а если нестрогое (со знаком ≤ или ≥), то ставят обычную точку. Эта точка разбивает координатную прямую на два промежутка (−∞, x0) и (x0, +∞).
Слайд 4
3. Определяются знаки функции y=a·x+b на этих промежутках. Для этого
вычисляется значение этой функции в любой точке промежутка (−∞, x0),
и знак этого значения и будет искомым знаком на промежутке (−∞, x0). Аналогично, знак на промежутке (x0, +∞) совпадает со знаком значения функции y=a·x+b в любой точке этого промежутка. Но можно обойтись без этих вычислений, а выводы о знаках сделать по значению коэффициента a: если a>0, то на промежутках (−∞, x0) и (x0, +∞) будут знаки − и + соответственно, а если a>0, то + и −.
4. Если решается неравенство со знаками > или ≥, то ставится штриховка над промежутком со знаком плюс, а если решаются неравенства со знаками < или ≤, то – со знаком минус. В результате получается геометрическое изображение числового множества, которое и является искомым решением линейного неравенства
Слайд 5
Решите неравенство −3·x+12>0.
1. Согласно алгоритму, сначала находим корень уравнения −3·x+12=0, −3·x=−12, x=4.
Дальше изображаем координатную прямую и отмечаем на ней точку
с координатой 4, причем эту точку делаем выколотой, так как решаем строгое неравенство:
Слайд 6
3. Теперь определяем знаки на промежутках. Для определения
знака на промежутке (−∞, 4) можно вычислить значение функции y=−3·x+12, например, при x=3.
Имеем −3·3+12=3>0, значит, на этом промежутке знак +. Для определения знака на другом промежутке (4, +∞) можно вычислить значение функции y=−3·x+12, к примеру, в точке x=5. Имеем −3·5+12=−3<0, значит, на этом промежутке знак −. Эти же выводы можно было сделать на основании значения коэффициента при x: так как он равен −3, то есть, он отрицательный, то на промежутке (−∞, 4) будет знак +, а на промежутке (4, +∞) знак −. Проставляем определенные знаки над соответствующими промежутками:
Слайд 7
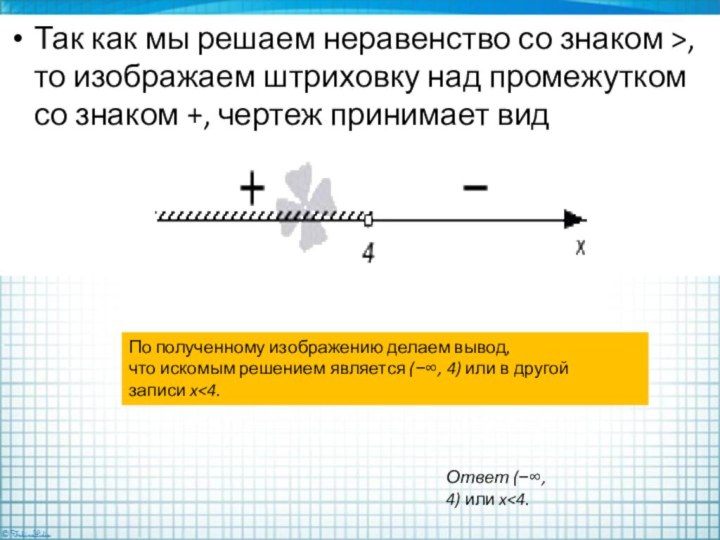
Так как мы решаем неравенство со знаком >,
то изображаем штриховку над промежутком со знаком +, чертеж
принимает вид
По полученному изображению делаем вывод,
что искомым решением является (−∞, 4) или в другой записи x<4.
Ответ (−∞, 4) или x<4.
Слайд 8
Тест
1. Какие из чисел –0,5; –1; 1 и
0,5 являются решением неравенства –3х – 4 > х
– 1?
а) 0,5; 1; б) –1; –0,5; в) -1; г) –0,5; 1; 0,5.
3. Известно, что а > b, какое из следующих неравенств неверно?
а) а + 5 > b + 5; в) а – 5 < b – 5;
б) –5а < –5b; г)
Слайд 9
3. Решите неравенство.
Х -
а) (–∞; 1,5]; в) [–1,5; +∞);
б)
[–0,9; +∞); г) (–∞; 0,9].
4. При каких значениях m имеет
смысл выражение ?
а) в)
б) г)
Слайд 11
Переменные, входящие в состав алгебраической дроби, принимают лишь
допустимые значения,
т.е. такие значения, при которых
знаменатель дроби
не обращается в нуль
Найти значение алгебраической дроби:
Решение:
Повторим. Пример №1:
если: а) а=2, b=1; б) а=5, b=0; в) а=4, b=4.
в) а=4, b=4:
На 0 делить нельзя!
Слайд 12
Находят значение переменной, при
которых знаменатель дроби
обращается
в нуль.
2. Затем исключают эти значения из множества
всех чисел.
Алгоритм нахождения допустимых значений дроби:
Слайд 13
Установите, при каких значениях переменной
не имеет смысла
дробь:
Ответ: при а = – 5
Решение
Слайд 14
при х ≠ – 2;
Установите, при каких
значениях
переменной имеет смысл дробь:
при х ≠ 0;
при
х ≠ 2;
х – любое число;
Слайд 15
Установите, при каких значениях переменной
имеет смысл дробь:
Ответ:
Решение
(3t – 2)(3t + 2) = 0,
(3t – 2)
= 0
3t = 2
или
(3t + 2) = 0,
3t = – 2,







![Презентация по алгебре на тему решение неравенств. Метод интервалов 3. Решите неравенство.Х - а) (–∞; 1,5]; в) [–1,5; +∞);б) [–0,9; +∞); г) (–∞; 0,9].4.](/img/tmb/7/655219/81b90e0f0e47721134c6bf8d10d2cd94-720x.jpg)