- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Кусочно-заданные функции, 9 класс
Содержание
- 2. Кусочно-заданные функции. щелкните
- 3. ОПРЕДЕЛЕНИЕ.Кусочно-заданная функция — функция, определённая на множестве вещественных чисел заданная на каждом из интервалов, составляющих область определения, отдельной формулой.
- 4. Формальное определение и задание функции.Пусть заданы
- 5. Запись кусочно-заданной функции.,,.f (x)=
- 6. Виды кусочно-заданных функций Если все функции — постоянные,
- 7. Построение графиков кусочно-заданных функций.f(x)=x=0 -является точкой смены формул.
- 8. f(x)=-xf(x)= x
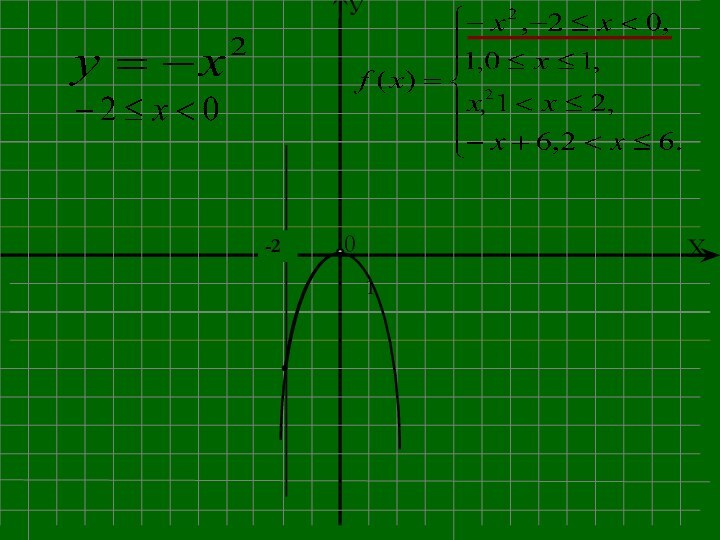
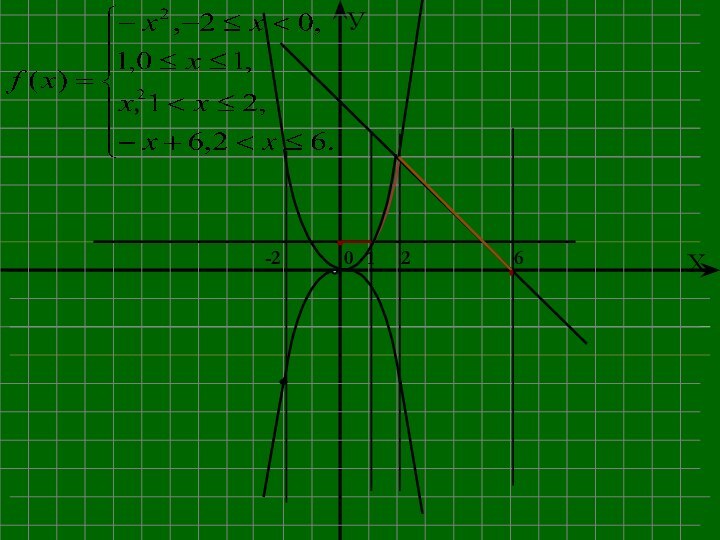
- 9. Построить график функции., x = -2; 0; 1; 2; 6 - точки смены формул.
- 10. -2 ,
- 11. 1,
- 12. ,2
- 13. ,,26
- 14. ,-226
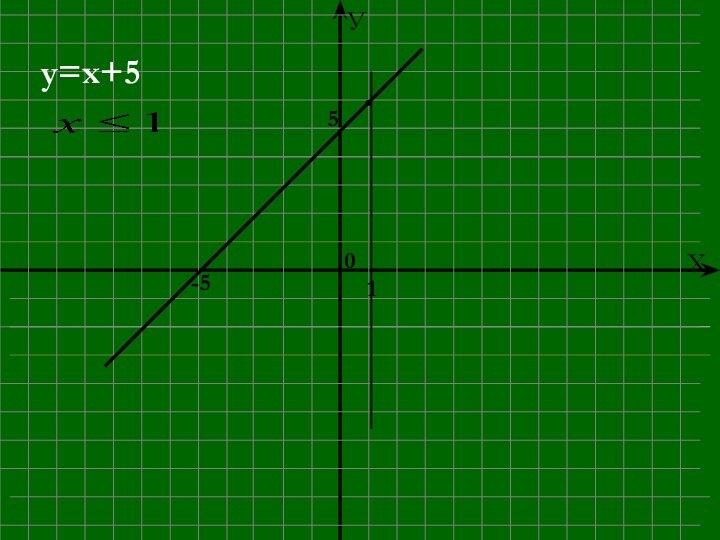
- 15. Построить график функцииX = 1; 4; 7 – точки смены формул.
- 16. y=x+5 -55
- 17. 24
- 18. 3740
- 19. -5537
- 20. Скачать презентацию
- 21. Похожие презентации
Кусочно-заданные функции. щелкните










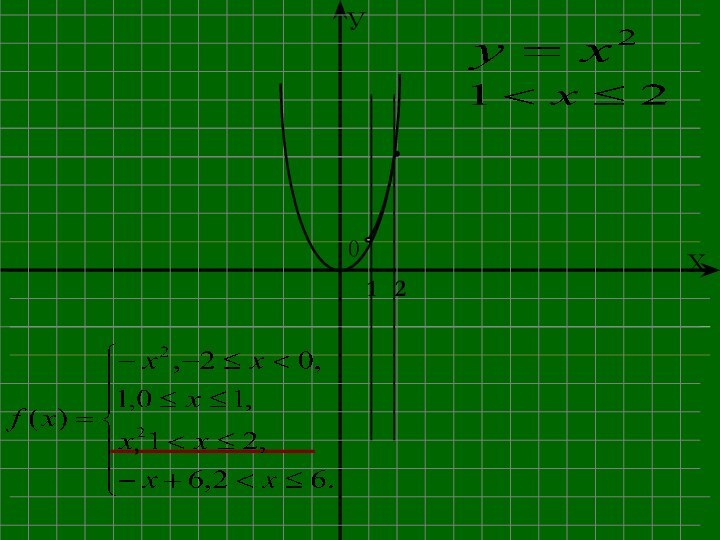



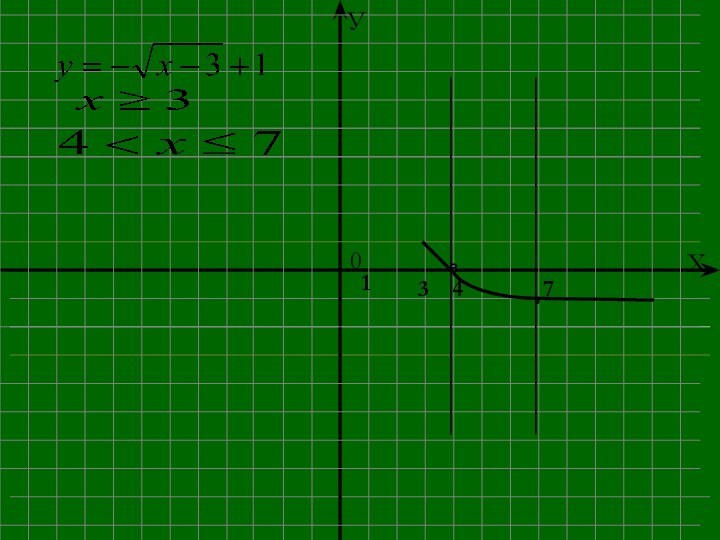


Слайд 3
ОПРЕДЕЛЕНИЕ.
Кусочно-заданная функция — функция, определённая на множестве вещественных чисел заданная
на каждом из интервалов, составляющих область определения, отдельной формулой.
Слайд 4
Формальное определение и задание функции.
Пусть заданы
— точки смены формул.
Кусочно-заданные функции, обычно задают на каждом из интервалов
отдельно .
Записывают это в виде:
Слайд 6
Виды кусочно-заданных функций
Если все функции — постоянные, то f(x) — кусочно-постоянная
функция.
Если все функции fi(x) являются линейными функциями, то f(x) — кусочно-линейная функция.
Если все функции fi(x) являются непрерывными функциями,
то f(x) — кусочно-непрерывная функция. При этом сама она может не являться непрерывной.Если все функции fi(x) являются дифференцируемыми функциями, то f(x) —кусочно-гладкая функция. При этом точки смены формул могут быть (а могут и не быть) точками излома.
Если все функции fi(x) являются монотонными функциями, то f(x) —кусочно-монотонная функция. При этом на соседних интервалах монотонность может быть разной.