Презентация на тему Исследовательская работа по математике Красивые задачи

Содержание

2. «Красивые» задачи.
3. Цель нашего исследования – создать сборник «красивых» математических
4. Объект исследования – решение математических
5. Задача построенная с помощью циркуля
7. Классификация задач по
8. Решение. Пусть А, В, С, D –
9. Задача Зигзаг разделил правильный девятиугольник на треугольники, как
10. ЗадачаДана белая доска размером 100*100 клеток. Двое
13. Скачать презентацию
14. Похожие презентации

«Красивые» задачи.

Главная
Алгебра
Исследовательская работа по математике Красивые задачи

«Красота математики, как и красота любой вещи, — это внутреннее свойство, она происходит из

Цель нашего исследования – создать сборник «красивых» математических задач. Задачи:Определить понятие «красивая» задача в

Объект исследования – решение математических задач. Предмет исследования – математические задачи определенного

Исследовательская работа по математике Красивые задачи

Классификация задач по группам:1) «Красивые» задачи по решению;2)

Решение. Пусть А, В, С, D – концы исходных ножек табуретки, а

Задача Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая часть

ЗадачаДана белая доска размером 100*100 клеток. Двое по очереди красят ее клетки

Слайды презентации

Слайд 2 «Красивые» задачи.

Слайд 3 Цель нашего исследования – создать сборник «красивых» математических задач.
Задачи:
Определить

Цель нашего исследования – создать сборник «красивых» математических задач. Задачи:Определить понятие «красивая» задача

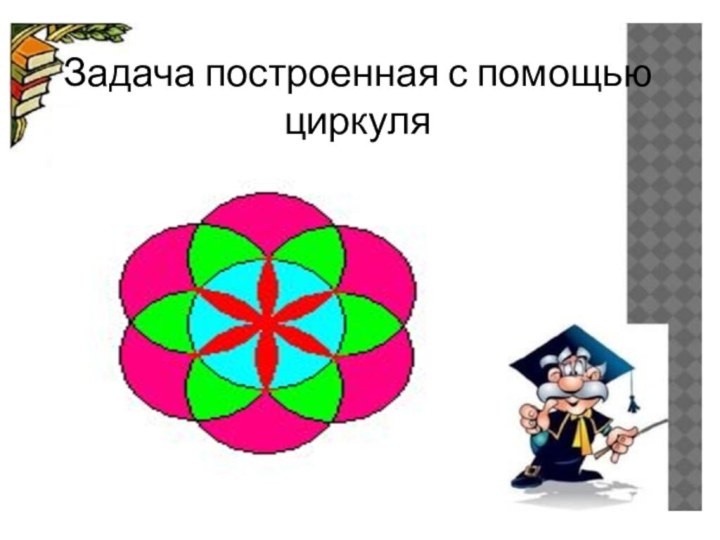
понятие «красивая» задача в математике.
Классифицировать найденные задачи

по разделам.
Подготовить материалы для сборника «красивых» математических задач.

Слайд 4
Объект исследования – решение математических задач.

Предмет

исследования – математические задачи определенного типа.

Гипотеза исследования – если окажется возможным

из множества математических задач выбрать определенные («красивые») задачи и классифицировать их по некоторым признакам, то возможно создание сборника таких задач и использование его в качестве математического саморазвития.
Методы исследования:
1.Теоретические.
2.Эмпирические.
3.Математические.

Слайд 5 Задача построенная с помощью циркуля

Слайд 6

Слайд 7 Классификация задач по группам:
1)

Классификация задач по группам:1) «Красивые» задачи по решению;2) «Красивые»

«Красивые» задачи по решению;
2) «Красивые» задачи по чертежу;
3) «Красивые»

задачи по содержанию;
4) «Красивые» олимпиадные задачи.

Слайд 8 Решение. Пусть А, В, С, D – концы

Решение. Пусть А, В, С, D – концы исходных ножек табуретки,

исходных ножек табуретки, а А1, В1, С1, D1 –

подпиленных. А1А + В1В = С1С + D1D. Поскольку табуретка стоит, касаясь пола четырьмя ножками, то точки А1, В1, С1 и D1 лежат в одной плоскости. Табуретка квадратная, значит, плоскости АВА1В1 и СDС1D1 параллельны. Следовательно, А1В1 // С1D1. Аналогично, В1С1 // А1D1. Таким образом, четырехугольник А1В1С1D1 – параллелограмм, и его диагонали пересекаются в точке О1. Пусть О – центр квадрата АВСD. Заметим, что отрезок ОО1 – средняя линия как в трапеции АСС1А1, так и в трапеции ВDD1В1, а значит , А1А+ С1С= 2ОО1= В1В+ D1D.
Теперь переберем возможные длины отпиленной части, расположенной по диагонали от потерянной. При этом получим, что длина отпиленной части удовлетворяет одному из равенств:
8+x=9+10, 9+x=8+10, 10+x=8+9, x=7, x=9,x=11.
Поскольку длины всех кусков различны, =9, и остаются только варианты 7 и 11.
Ответ: 7,11.

Маленький Петя подпилил все ножки у квадратного табурета и четыре отпиленных кусочка потерял. Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек?

Слайд 9 Задача
Зигзаг разделил правильный девятиугольник на треугольники, как показано

Задача Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая

на рисунке. Какая часть площади больше: закрашенная или незакрашенная?

Решение.

Проведем в девятиугольнике еще несколько диагоналей.

Девятиугольник разбился на 13 треугольников. На рисунке
образовалось много параллелограммов и трапеций с
диагоналями. Расставим номера треугольников, причем
одинаковым номером отметим равные треугольники разных
цветов. 12 из них разбились на пары, а тринадцатому,
который оказался закрашенным, пары не хватило. Значит,
закрашенная часть площади девятиугольника больше
его незакрашенной части.
Ответ: закрашенная.

Слайд 10 Задача
Дана белая доска размером 100*100 клеток. Двое по

ЗадачаДана белая доска размером 100*100 клеток. Двое по очереди красят ее

очереди красят ее клетки в черный цвет, причем первый

всегда закрашивает квадрат 2*2, а второй—три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?
Ответ: второй

Решение. В одном из углов доски второй игрок своим первым ходом закрашивает три клетки в прямоугольнике 2x3, а три оставшиеся клетки из этого прямоугольника объявляет резервом. В дальнейшем второй игрок делает все возможные ходы, не затрагивая резерва. Если такой ход становится невозможным, то закрашиваются клетки резерва. Ясно, что ответного хода у первого игрока нет.