Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Что такое степень с натуральным показателем

Содержание

2. Найдите значения выражений:3+3+3+3=2+2+2+2+2+2+2=Упростите выражение:х+х+х+…+х+х= п слагаемых
3. Найдите площадь квадрата со стороной 10 см.
4. 1)10 · 10
5. Степень с натуральным показателем
6. Степень с натуральным показателем ап =а•а•а•…•а•апоказатель степениn множителейоснование степени56; 3,75; 04; (-4,8)6
7. Степенью числа а с натуральным показателем
8. №1. Представьте в виде произведения
9. №3. Вычислите:
10. № 5. Найдите х, если2х = 32;
11. №7: Сравните с нулём значения выражений
12. (-2)1 =(- 2) = -2(-2)2 = (-
14. 5) -24 и (-2)4
15. 1) а4; 34 = 812) 0,251 =
16. Из истории степеней
17. Сложение, вычитание, умножение и деление
19. Вильям Оутред (1575-1660)– английский математикAq вместо A2Ac вместо A3Aqqвместо A4
20. Франсуа Виет (1540-1603) – французский матемматикВиет применял
21. Михаэль Штифель (1487г.-19.04.1567г.) -немецкий математик ААА вместо А3
22. Томас Гарриот (1560-1621)-английский математикаааа вместо а4
23. Рене Декарт (1596-1650) –французский математик Рене Декарт в его «Геометрии» (1637) впервые ввёл современное обозначение степеней
24. В физике:10 = 101100 = 102 (санти)
26. В астрономии расстояния до звезд измеряют в
27. Миаил Васильевич Ломоносов (1711-1765)-русский учёный“Пусть кто-нибудь попробует
28. Скачать презентацию
29. Похожие презентации

Найдите значения выражений:3+3+3+3=2+2+2+2+2+2+2=Упростите выражение:х+х+х+…+х+х= п слагаемых

Главная
Алгебра
Что такое степень с натуральным показателем

N –натуральные числаZ – целые числаQ - рациональные числа

Найдите значения выражений:3+3+3+3=2+2+2+2+2+2+2=Упростите выражение:х+х+х+…+х+х= п слагаемых

Найдите площадь квадрата со стороной 10 см. Найдите объем куба с

Степень с натуральным показателем ап =а•а•а•…•а•апоказатель степениn множителейоснование степени56; 3,75; 04; (-4,8)6

Степенью числа а с натуральным показателем n(п≥ 2)называется произведение n множителей,

№1. Представьте в виде произведения третью степень числа 4 и

№7: Сравните с нулём значения выражений (-3) 4 + (-81)(-6)

(-2)1 =(- 2) = -2(-2)2 = (- 2) (- 2) = 4(-2)3

1) а4; 34 = 812) 0,251 = 0,253) 0100 = 04) 125

Из истории степеней У древних вавилонян,

Сложение, вычитание, умножение и деление идут первыми в списке арифметических

Вильям Оутред (1575-1660)– английский математикAq вместо A2Ac вместо A3Aqqвместо A4

Франсуа Виет (1540-1603) – французский матемматикВиет применял сокращения:N для первой степени,Q для

Михаэль Штифель (1487г.-19.04.1567г.) -немецкий математик ААА вместо А3

Томас Гарриот (1560-1621)-английский математикаааа вместо а4

Рене Декарт (1596-1650) –французский математик Рене Декарт в его «Геометрии» (1637) впервые ввёл современное обозначение степеней

В физике:10 = 101100 = 102 (санти) 1000 = 103 (кило)1000000 =

Что такое степень с натуральным показателем

В астрономии расстояния до звезд измеряют в астрономических единицах (а.е.).1 а.е. =

Миаил Васильевич Ломоносов (1711-1765)-русский учёный“Пусть кто-нибудь попробует вычеркнуть из математики степени, и

Найти значение выражения n2 + k2 , если 2n = 32

Слайды презентации

Слайд 2 Найдите значения выражений:
3+3+3+3=
2+2+2+2+2+2+2=
Упростите выражение:
х+х+х+…+х+х=
п слагаемых

Слайд 3 Найдите площадь квадрата со стороной 10 см.

Найдите объем куба с ребром 0,5 см.

S = а2
S

= 102 = 100(см2)

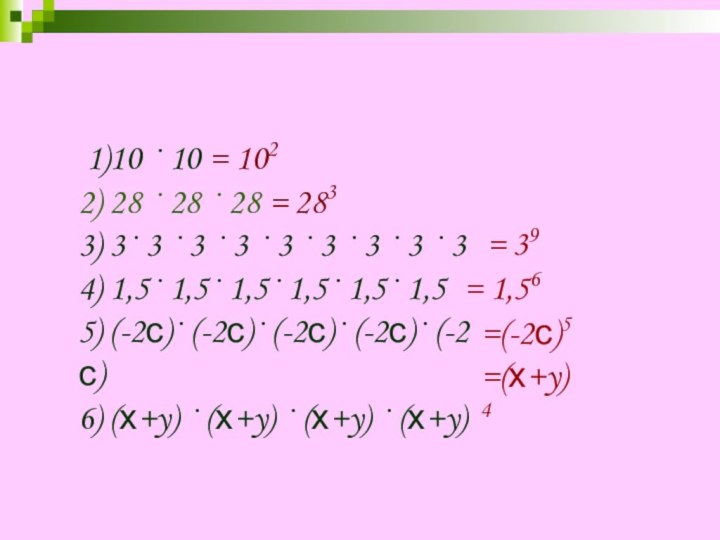
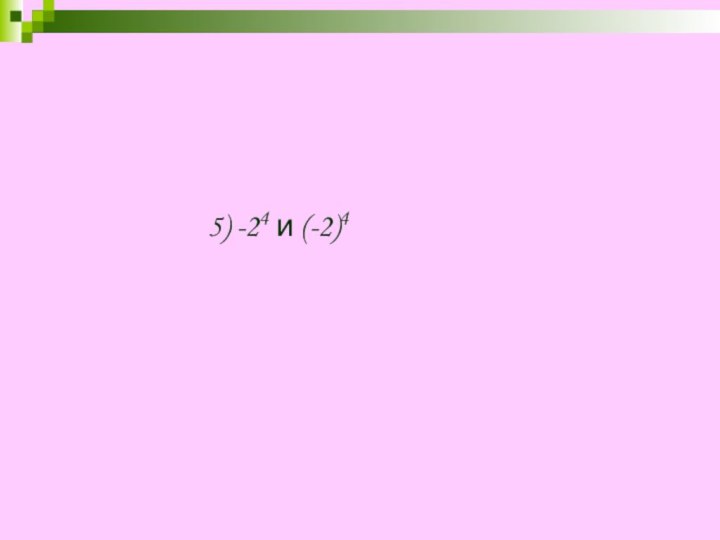
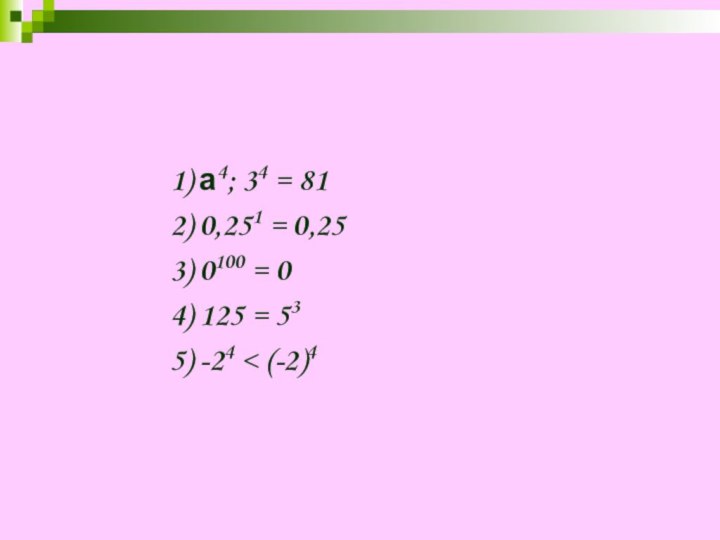
V = а3
V = 0,53= 0,125 (см3)

Слайд 4

1)10 · 10 =

102
2) 28 · 28 · 28 = 283
3) 3·

3 · 3 · 3 · 3 · 3 · 3 · 3 · 3
4) 1,5· 1,5· 1,5· 1,5· 1,5· 1,5
5) (-2с)· (-2с)· (-2с)· (-2с)· (-2с)
6) (х+y) · (х+y) · (х+y) · (х+y)

= 39

=(-2с)5

= 1,56

=(х+y)4

Слайд 5 Степень с
натуральным
показателем

Слайд 6 Степень с натуральным показателем
ап =а•а•а•…•а•а

показатель

степени
n множителей
основание степени
56; 3,75; 04; (-4,8)6

Слайд 7 Степенью числа а с натуральным показателем n(п≥

Степенью числа а с натуральным показателем n(п≥ 2)называется произведение n

2)называется произведение n множителей, каждый из которых равен а.
Степенью

числа а с показателем 1 называется само число а. (а1=а)
Операцию отыскания степени называют возведением в степень.

Слайд 8
№1. Представьте в виде произведения
третью степень

числа 4 и найдите
ее числовое значение.
43 = 4·4·4 =64

№2. Чему равна сумма кубов чисел 5 и 3 ?
53 + 33 = 125 + 27 =152

Слайд 9

№3. Вычислите:

1) 5 3

2) 24 – 62
3) (-4) 2+ 25
4) 1 7 – 92 + 10 3
№4. Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1.
1) 64 2)36 3)121 4)27

= 125

= -20

= 48

= 920

=43

=62

=112

=33

Слайд 10

№ 5. Найдите х, если

2х = 32;

2) х 3 = 125

№ 6. Вычислите

квадрат
куба числа:
1)2 2)4

2 х= 25

х=5

х 3= 53

х = 5

(23) 2 =64

(43)2=4096

Слайд 11 №7: Сравните с нулём значения выражений

(-3) 4 + (-81)

(-6) 2 – 12

4 2 ·

(-1) 5

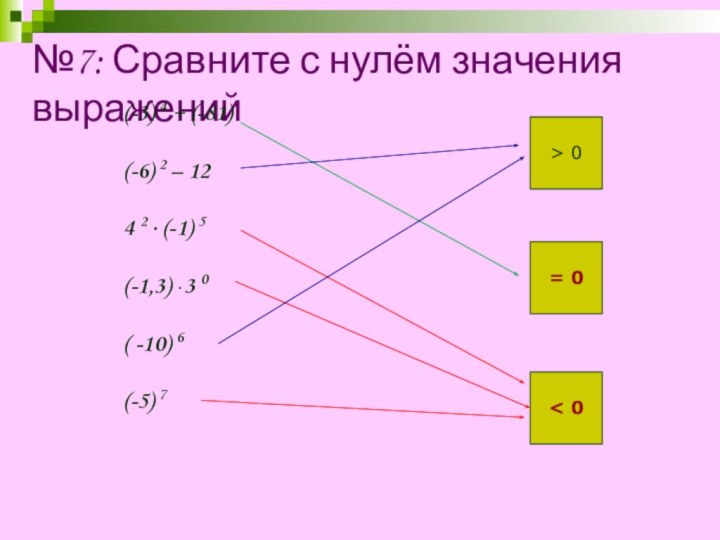
(-1,3) · 3 0

( -10) 6

(-5) 7

> 0

= 0

< 0

Слайд 12 (-2)1 =(- 2) = -2
(-2)2 = (- 2)

(- 2) = 4
(-2)3 = (- 2) (- 2)

(- 2) = -8
(-2)4 = (- 2) (- 2) (- 2) (- 2) = 16
(-2)5 = (- 2) (- 2) (- 2) (- 2) (- 2) = -32
(-2)6 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = 64
(-2)7 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = -128
(-2)8 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = 256
(-2)9 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = -512
(-2)10 = (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) (- 2) = 1024

Какую закономерность
можно заметить?

Слайд 13

an

n - четное
a >

an > 0

a = 0

an = 0

a < 0

n - нечетное

an < 0

Слайд 14
5) -24 и (-2)4

Слайд 15
1) а4; 34 = 81
2) 0,251 = 0,25
3)

1) а4; 34 = 812) 0,251 = 0,253) 0100 = 04)

0100 = 0
4) 125 = 53
5) -24 < (-2)4

Слайд 16 Из истории степеней

Из истории степеней У древних вавилонян, египтян и

У древних вавилонян, египтян и китайцев имелись

некоторые отдельные знаки – иероглифы для немногих математических понятий. Однако лишь в «Арифметике » Диофанта (3в) встречаются зачатки алгебраической буквенной символики.

Слайд 17
Сложение, вычитание, умножение и деление идут

первыми в списке арифметических действий. У математиков не сразу

сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.

Слайд 18

Европейские

Европейские математики 16 века вторую степень неизвестного

математики 16 века вторую степень неизвестного называли «сила», а

также «квадрат», третью степень – «куб».
Немецкие математики Средневековья стремились ввести единое обозначение и сократить число символов. Книга Михаэля Штифеля «Полная арифметика» (1544 г.) сыграла в этом значительную роль.