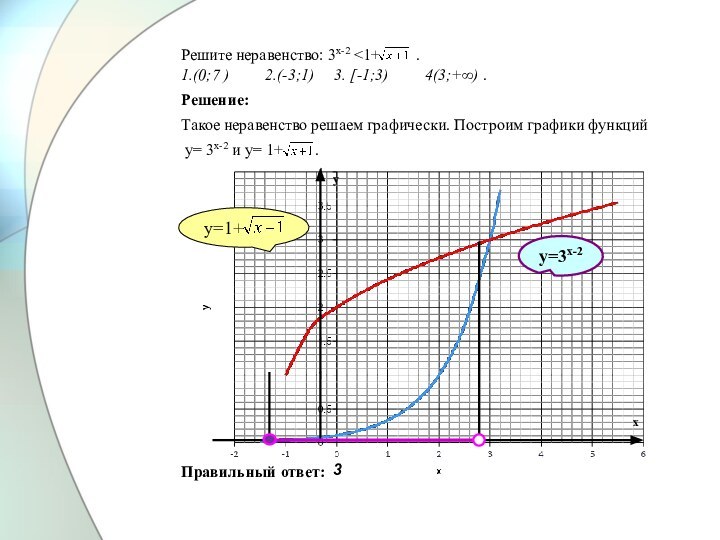
≤4х .
1.[1;6]
2.[2;3] 3.(-∞;2]U[3; +∞) 4. (-∞;1]U[6; +∞)
Решение:
Поскольку 4х =22х , получим: 2 ≤ 22х.
Т.к. основание степени равно 2 и оно больше 1, то это неравенство равносильно неравенству того же смысла:
х2 -5х+6≤2х.
Перенесём 2х из правой части неравенства в левую с противоположным знаком:
х2 -5х+6-2х≤0,
приведём подобные члены:
х2 -7х+6≤0.
Рассмотрим функцию у = х2-7х+6. Графиком этой функции является парабола, ветви которой направлены вверх. Выясним, как расположена эта парабола относительно оси х. Для этого решим уравнение х2-7х+6=0.
Получим: х1=6, х2=1.
Значит, парабола пересекает ось х в двух точках, абсциссы которых равны 1 и 6. Покажем схематически, как расположена парабола в координатной плоскости.
Из рисунка видно, что функция принимает неположительные значения на [1;6].
Правильный ответ:
1
Х
1
6


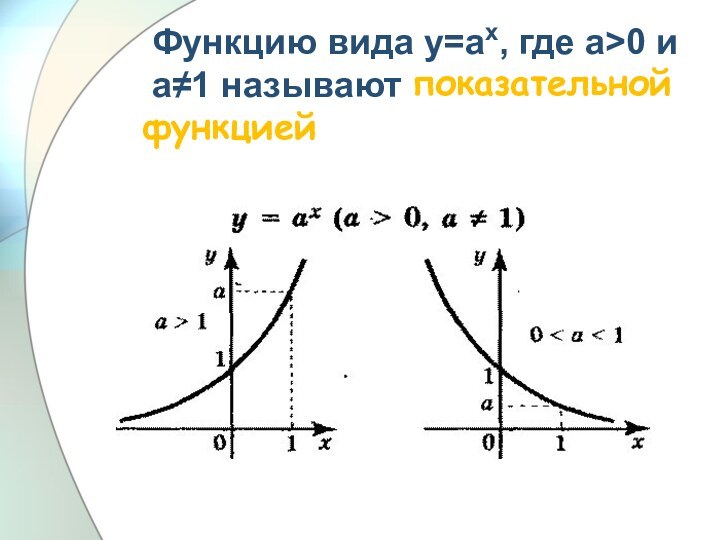



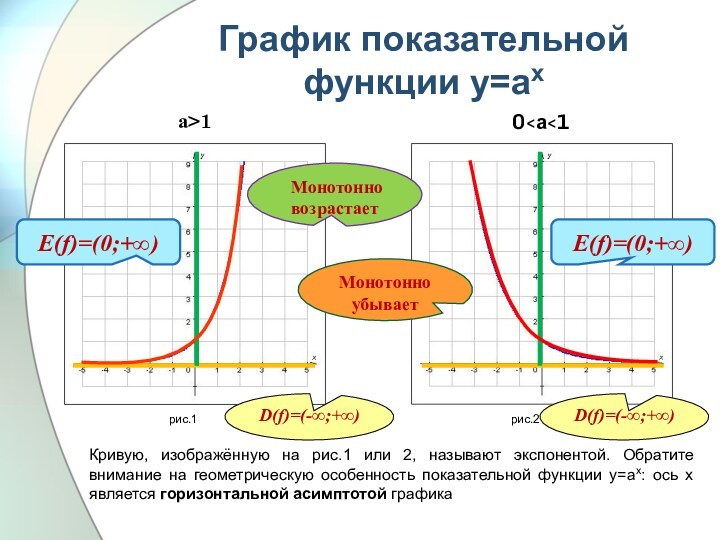


![Презентация к уроку по математике Решение показателных неравенств А.6. Решите неравенство: 37х-9 ≤ 81х .1. (-∞; 1,5]](/img/tmb/6/515329/5bb2e7c78b5ddf3de7e0fad10a42755e-720x.jpg)


![Презентация к уроку по математике Решение показателных неравенств Задания для самостоятельного решенияРешите неравенства:№1. 4≥16х+1 1.(-∞; 1,5]](/img/tmb/6/515329/a49c613ebe4a7a2d219d4a685cfcce87-720x.jpg)








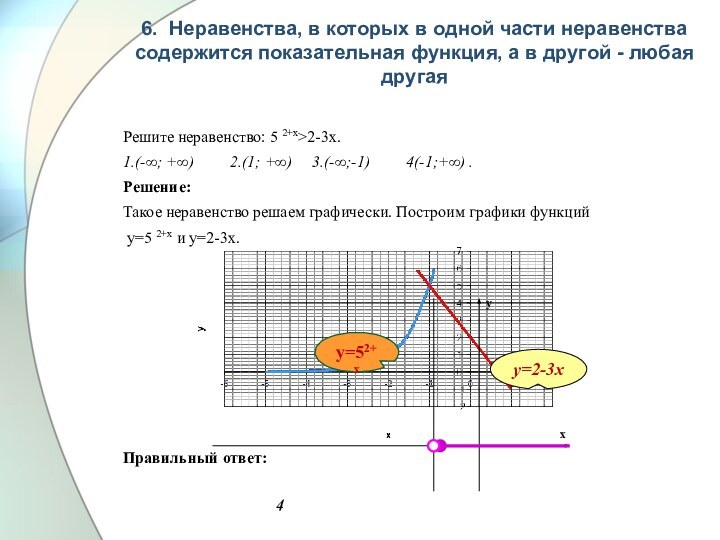
![Презентация к уроку по математике Решение показателных неравенств Решите неравенство: 5х-4≤(х-2)2.1.(-1;3] 2.( -∞;1]](/img/tmb/6/515329/d73746a7a595f0a7cbb470f272837bc6-720x.jpg)