Презентация на тему к циклу уроков по алгебре в 11 классе по теме Комбинаторика

вероятность наступления какого – либо события?
Можно ли вычислить вероятность

- благоприятные исходы

- все возможные исходы

конвертам?
1
2
3
4
5
6
7
8
9
10
?

в которой изучаются
вопросы о том, сколько различных комбинаций,

все нужные
нам комбинации и непосредственно подсчитать их.
При переборе

Обозначаем наши комбинации буквами или цифрами так,
что каждая комбинация будет обозначена своей уникальной
последовательностью букв или цифр.

Выписываем комбинации в алфавитном порядке (при
обозначении буквами) или по возрастанию (при обозначении
цифрами).

в ресторан отдали свои шляпы
швейцару, а при выходе

4
и также занумеруем их шляпы. Считаем, что
шляпа с

Всего 9 вариантов требуемой раздачи шляп.

1

2

3

4

важен для нас, а в некоторых не важен.
Упорядоченный набор

Всякий неупорядоченный набор
объектов – множество, сами
объекты – элементы множества.

Пример: слово автор является
цепочкой из 5 элементов:
а, в, т, о и р.

А U В
состоит из всех
элементов хотя
бы одного

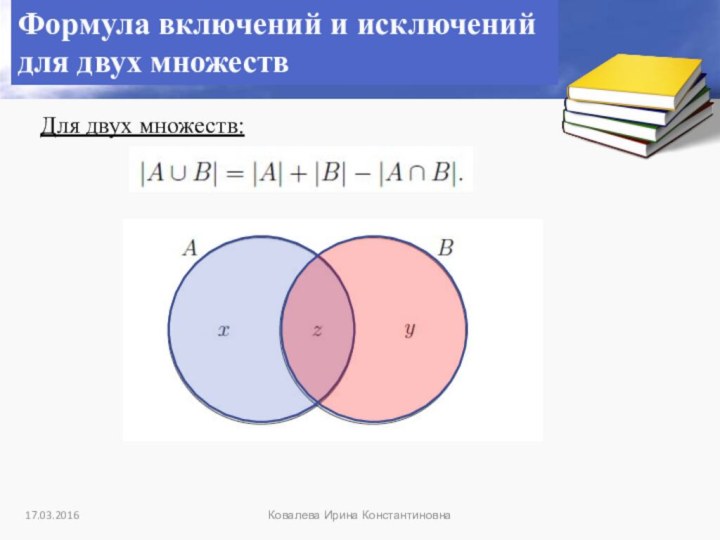
Множество А ∩ В
состоит только из
общих элементов
множества А и В

Множество А \ В
состоит из всех
элементов множества
А не принадлежащих
множеству В

Пример:
А{1,2,3,4,5,6}
В{5,6,7,8,9}
АUВ{1,2,3,4,5,6,7,8,9}

Пример:
А{1,2,3,4,5,6}
В{5,6,7,8,9}
А∩В{5,6}

Пример:
А{1,2,3,4,5,6}
В{5,6,7,8,9}
А\В{1,2,3,4}

a можно
выбрать m способами, а объект b –

Сколькими способами можно
выбрать фрукт с подноса?

Яблоко – 5 способами,
сливу – 5 способами,
клубнику – 4 способами.

Ответ: 14 способами.

a
можно выбрать m способами, после чего объект b

В магазине есть 7 видов пиджаков,
3 вида брюк, 4 вида галстуков.
Сколькими способами можно купить
комплект из пиджака, брюк и галстука?

7*3*4 = 84

друга только порядком следования элементов, называются перестановками.

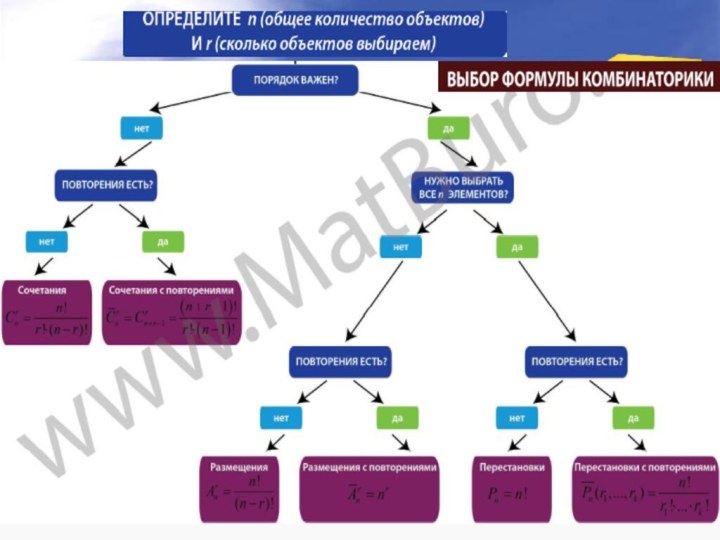
Число перестановок из n-элементов вычисляется по формуле:
Рn = n!

способами их можно рассадить?


Р8= 8!= 8*7*6*5*4*3*2*1

друг от друга составом и порядком, называются размещениями.

составить двузначных чисел?

нужно выбрать капитана и его заместителя. Сколькими способами это

9 предметов. Сколькими способами можно составить расписание на понедельник,

7. Решите уравнение

выбираемых из m различных видов, и отличающиеся одно от

Читают: число размещений с повторениями
из эм по эн

без повторений
Размещения
с повторениями
-расположение

расположение «предметов»
в предложении так, что
каждый предмет может
участвовать в размещении
сколько угодно раз.

22232223
22333223
33322322
23232323
32232232и т.д.

только составом элементов, называются сочетаниями из n-элементов по к.

в каждом ( n m) называются такие соединения, каждое

коктейлей можно получить, если для каждого берутся три сока?

задачи?

можно извлечь последовательно 6 звуков?
2.Сколькими способами можно рассадить 5

3.Сколько четырёхзначных чисел можно составить из четырёх
карточек с цифрами 0, 5, 7, 9?

4.В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

5.Студенческая группа состоит из 23 человек, среди которых
10 юношей и 13 девушек. Сколькими способами можно выбрать
двух человек одного пола?

задача решается
непосредственным применением комбинаторных
принципов – правила суммы

В некоторых случаях приходится идти окольным путем и
действовать «методом решета»: для нахождения элементов
интересующего нас множества мы сначала находим число
элементов некоторого большего множества, а потом
«просеиваем» нужные элементы, постепенно отбрасывая
лишние.

для двух множеств

множеств

задачу о шляпах в общем виде.
Задача (Леонард Эйлер): Войдя

Решение:
занумеруем гостей числами 1, 2, …, n и так же занумеруем
шляпы (при этом i-ая шляпа принадлежит i-му гостю).
Тогда каждый вариант разбора шляп обозначается
единственной перестановкой чисел 1, 2, …, n.

число i стоит на
своем месте, если ki =i

Пусть Аi - множество перестановок, в которых число i стоит
на своем месте (i = 1,2,…,n). Искомое число N беспорядков,
таким образом равно

|Аi| = (n – 1)!, поэтому