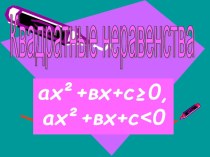Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Квадратичная функция

Содержание

План:1 Определение квадратичной функции2 Свойства функции3 Графики функции4 Квадратичные неравенства5 Вывод
Квадратичная функция.Подготовил ученик 8А класса Герлиц Андрей. План:1 Определение квадратичной функции2 Свойства функции3 Графики функции4 Квадратичные неравенства5 Вывод Определение:Квадратичной функцией называется функция, которую можно записать формулой вида y = ax2 Свойства: Свойства функции и вид ее графика определяются, в основном, значениями - Четность, нечетность:при b= 0     функция четнаяпри b≠0    функция не является ни -Промежутки монотонности при а > 0  График:           Графиком квадратичной функции является парабола – кривая, симметричная относительно прямой , Чтобы построить график квадратичной функции, нужно: 1)найти координаты вершины параболы и Неравенства:Неравенства вида ах2 + bх + с > 0 и ах2 + Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, Вывод: Квадратичные функции используются уже много лет. Формулы решения квадратных уравнений
Слайды презентации

Слайд 2 План:
1 Определение квадратичной функции
2 Свойства функции
3 Графики функции
4

План:1 Определение квадратичной функции2 Свойства функции3 Графики функции4 Квадратичные неравенства5 Вывод

Квадратичные неравенства
5 Вывод

Слайд 3
Определение:
Квадратичной функцией называется функция, которую можно записать формулой

Определение:Квадратичной функцией называется функция, которую можно записать формулой вида y =

вида y = ax2 + bx + c, где

x – независимая переменная, a, b и c – некоторые числа, причем a≠0.

Слайд 4 Свойства:
Свойства функции и вид ее графика

Свойства: Свойства функции и вид ее графика определяются, в основном, значениями

определяются, в основном, значениями коэффициента a и дискриминанта.

-  Область определения: R;
- Область значений:
при а > 0          [-D/(4a); ∞)
при а < 0          (-∞; -D/(4a)];


Слайд 5
- Четность, нечетность:
при b= 0     функция четная
при b≠0   

- Четность, нечетность:при b= 0     функция четнаяпри b≠0    функция не является

функция не является ни четной, ни нечетной.
- Нули:
при

а < 0          (-∞; -D/(4a)];
при D > 0      два нуля:
при D = 0      один нуль:
при D < 0     нулей нет

Слайд 6
-Промежутки монотонности
при а >

-Промежутки монотонности при а > 0  при а < 0 

0 


при а < 0 


Слайд 7 График:
           Графиком квадратичной функции является парабола – кривая,

График:           Графиком квадратичной функции является парабола – кривая, симметричная относительно прямой

симметричная относительно прямой , проходящей через вершину параболы (вершиной

параболы называется точка пересечения параболы с осью симметрии).

Слайд 8
Чтобы построить график квадратичной функции, нужно:
1)найти

Чтобы построить график квадратичной функции, нужно: 1)найти координаты вершины параболы и

координаты вершины параболы и отметить ее в координатной плоскости;

2)построить еще несколько точек, принадлежащих параболе;
3)соединить отмеченные точки плавной линией.
           

Слайд 9 Неравенства:
Неравенства вида ах2 + bх + с >

Неравенства:Неравенства вида ах2 + bх + с > 0 и ах2

0 и ах2 + bх + с < 0,

где х — переменная, a, b и с — некоторые числа, причем, а≠0, называют неравенствами второй степени с одной переменной.

Слайд 10
Решение неравенства второй степени с одной переменной можно

Решение неравенства второй степени с одной переменной можно рассматривать как нахождение

рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция

принимает положительные или отрицательные значения.

  • Имя файла: kvadratichnaya-funktsiya.pptx
  • Количество просмотров: 155
  • Количество скачиваний: 0
- Предыдущая Слово и его формы. Родственные слова.
Следующая - Войны России в литературе

Похожие презентации

Презентация по алгебре на тему Стандартный вид многочлена (7 класс). Презентация по алгебре на тему Стандартный вид многочлена (7 класс). 185
Производная Производная 177
Неравенства и их системы. Неравенства и их системы. 157
Презентация к уроку: Системы линейных уравнений в физике Презентация к уроку: Системы линейных уравнений в физике 170
Презентация к уроку по алгебре Решение экологических задач методом составления системы уравнений Презентация к уроку по алгебре Решение экологических задач методом составления системы уравнений 141
КОВАЛЕВСКАЯ Софья Васильевна КОВАЛЕВСКАЯ Софья Васильевна 194
Решение линейных неравенств Решение линейных неравенств 170
Исследование графика линейной функции Исследование графика линейной функции 169
Решение неравенств методом интервалов Решение неравенств методом интервалов 159
Иррациональные уравнения Иррациональные уравнения 181
Неделя математики МИФ 2018-2019 учебный год Неделя математики МИФ 2018-2019 учебный год 161
Деление многочлена на многочлен Деление многочлена на многочлен 300
Уравнения с параметрами Уравнения с параметрами 141
Презентация Электронное пособие по тригонометрии Презентация Электронное пособие по тригонометрии 230
Решение простейших тригонометрических уравнений Решение простейших тригонометрических уравнений 139
Презентация по математике на тему Линейная функция ( 7 класс) Презентация по математике на тему Линейная функция ( 7 класс) 168
Формулы и правила дифференцирования Формулы и правила дифференцирования 182
Неопределенный интеграл Неопределенный интеграл 141
Презентация по алгебре Способы решения систем уравнений (7 класс) Презентация по алгебре Способы решения систем уравнений (7 класс) 166
Презентация к уроку по алгебре Неполные квадратные уравнения Презентация к уроку по алгебре Неполные квадратные уравнения 166
Интерактивный кроссворд Треугольники Интерактивный кроссворд Треугольники 174
Презентация по геометрии на тему Параллельность прямой и плоскости (10 класс) Презентация по геометрии на тему Параллельность прямой и плоскости (10 класс) 188
Презентация по алгебре на тему Линейная функция (7 класс) Презентация по алгебре на тему Линейная функция (7 класс) 188
Презентация Портрет показательной функции (алгебра, 11 класс) Презентация Портрет показательной функции (алгебра, 11 класс) 228
Презентация по алгебре: Арифметическая и геометрическая прогрессии (9 класс) Презентация по алгебре: Арифметическая и геометрическая прогрессии (9 класс) 155
Квадратные уравнения Квадратные уравнения 178
Координатная плоскость по алгебре (7 класс) Координатная плоскость по алгебре (7 класс) 177
План проведения семинара для учителей (по Муниципальному заданию на 2016 год) Реальная математика в Концепции развития математического образования План проведения семинара для учителей (по Муниципальному заданию на 2016 год) Реальная математика в Концепции развития математического образования 177
Лайфхак при решении заданий ЕГЭ. Лайфхак при решении заданий ЕГЭ. 183
Көпмүшені топтау тәсілімен көбейткіштерге жіктеу тақырыбына презентация (алгебра 7 сынып) Көпмүшені топтау тәсілімен көбейткіштерге жіктеу тақырыбына презентация (алгебра 7 сынып) 225