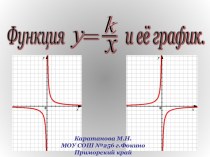
c=0
Неполная квадратное уравнении когда b=0,c≠0
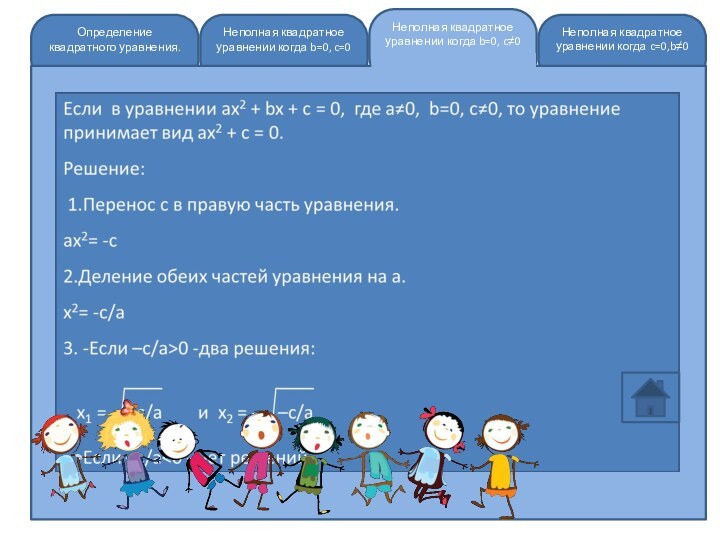
Неполная квадратное уравнении когда c=0,b≠0
,
Определение
квадратного уравненияПолное квадратное уравнение
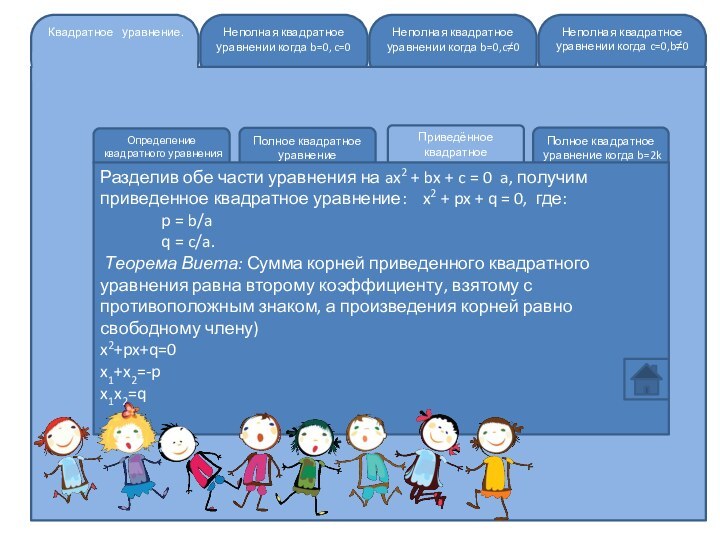
Приведённое квадратное уравнение
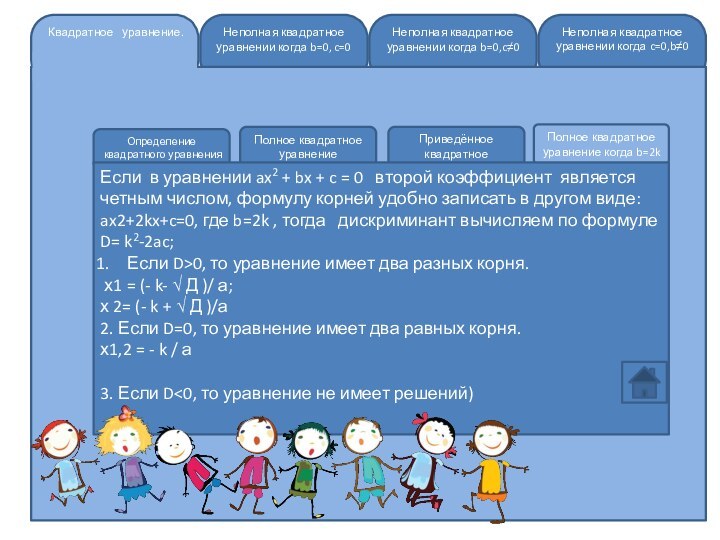
Полное квадратное уравнение когда b=2k
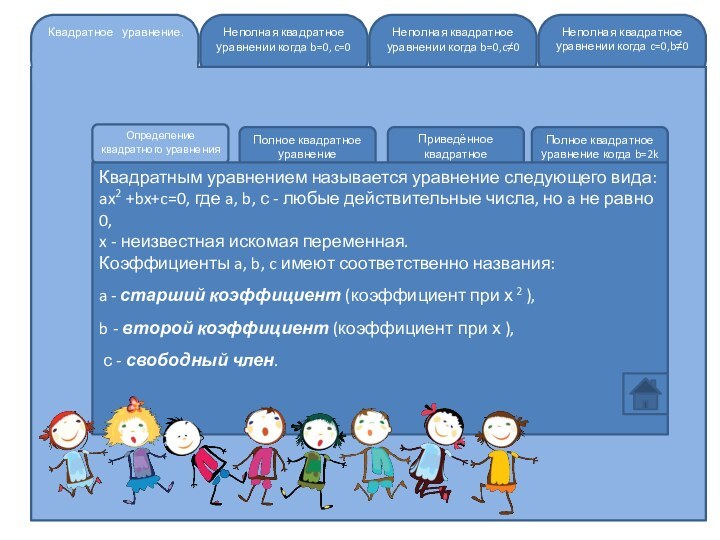
Квадратным уравнением называется уравнение следующего вида: ax2 +bx+c=0, где a, b, с - любые действительные числа, но a не равно 0,
x - неизвестная искомая переменная.
Коэффициенты a, b, c имеют соответственно названия:
a - старший коэффициент (коэффициент при х 2 ),
b - второй коэффициент (коэффициент при х ),
с - свободный член.