Слайд 2
УРОК №1
ТЕМА УРОКА: «РАЗМЕЩЕНИЯ»
Слайд 3
ТИП УРОКА: изучение нового материала.
ЦЕЛЬ: создать условия для
осознания и осмысления блока новой учебной информации.
ЗАДАЧИ:
Способствовать запоминанию
основной терминологии, умению вычислять перестановки и размещения;
Способствовать развитию интереса к математике, умений применять новый материал на практике и в жизни
Способствовать воспитанию аккуратности.
НОВЫЕ ПОНЯТИЯ: размещения, размещения с повторениями
ОБОРУДОВАНИЕ: доска, презентация
Слайд 4
"КВАРТЕТ"
«Проказница Мартышка, Осел, Козел да косолапый Мишка
задумали сыграть квартет ….»
Сколько существует способов, чтобы рассадить в
один ряд четырех музыкантов?
Задача №1
Слайд 5
"Конкурс"
Задача №2
Вас пригласили на конкурс красоты
с 8 участницами . Одновременно проводиться викторина: нужно угадать,
кто займет 1,2,3 место.
Сколько всего существует вариантов?
Слайд 6
Определение.
Размещением из n элементов по k (k≤n) называется
любое множество, состоящее из любых k элементов, взятых в
определенном порядке из данных n элементов.
Обозначение:
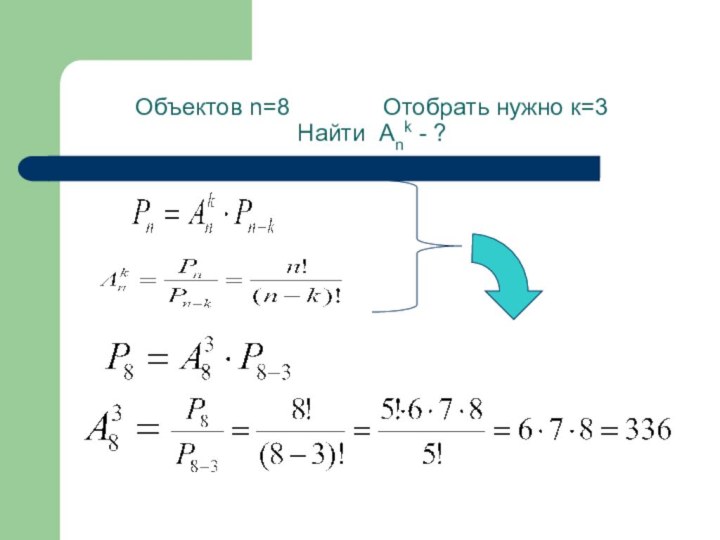
Отобрать нужно к=3
Найти Аnk - ?
Слайд 8
II способ решения:
Первое место может занять
любая из 8 участниц, второе место может занять любая
из оставшихся 7 участниц, третье место – любая из оставшихся 6 участниц. Тогда общее число способов равно:
Слайд 9
ТЕОРЕМА.
Ank =n(n – 1)(n – 2)…..(n –
k +1)
Доказательство: Выбрать один элемент из n элементов
можно n способами. Если этот выбор сделан, то второй элемент выбирается из (n -1) элементов, т.к. повторения запрещены, то третий элемент выбирают из (n– 2) элементов,… к-ый элемент (последний) из n – (к – 1) элементов.
По правилу произведения получим:
Ank =n(n – 1)(n – 2)…..(n – k +1).
Слайд 10
Задача № 3
У нас есть 9
разных книг из серии «Занимательная математика». Сколькими способами можно:
а) расставить их на полке;
б) подарить три из них победителям школьной олимпиады, занявшим первые три места?
Слайд 11
Решение:
а) P9= 9!= 362 880;
б)
Слайд 12
II. Закрепление материала. Решение задач.
Сколькими способами можно
составить трехцветный полосатый флаг из горизонтальных полос, если имеется
материал пяти различных цветов.
Из 9 членов комитета надо выбрать председателя, его заместителя и секретаря. Сколькими способами это можно сделать?
На соревнованиях по легкой атлетике приехала команда из 12 спортсменок. Сколькими способами тренер может определить, кто из них побежит в эстафете 4 х 100 м на первом, втором, третьем и четвертом этапах?
Слайд 15
Число размещений из n элементов по m с
повторениями.
Выбор m элементов подмножества из n– элементов множества
при условии, что элементы подмножества возвращаются в исходное множество – называется размещением с повторением
Число размещений из n элементов по m с повторениями обозначается
Слайд 16
Теорема:
Доказательство: Выбрать один элемент
из n элементов можно n способами. После того, как
этот выбор сделан, второй элемент опять выбирается из n элементов, т.к. повторения разрешены, третий…m-ый элемент также из n элементов. По правилу произведения
Пример: Сколько различных трехзначных чисел можно составить из цифр 1,2,3,4,5,6,7,8,9?