Презентация на тему по алгебре Квадратные уравнения (8класс)

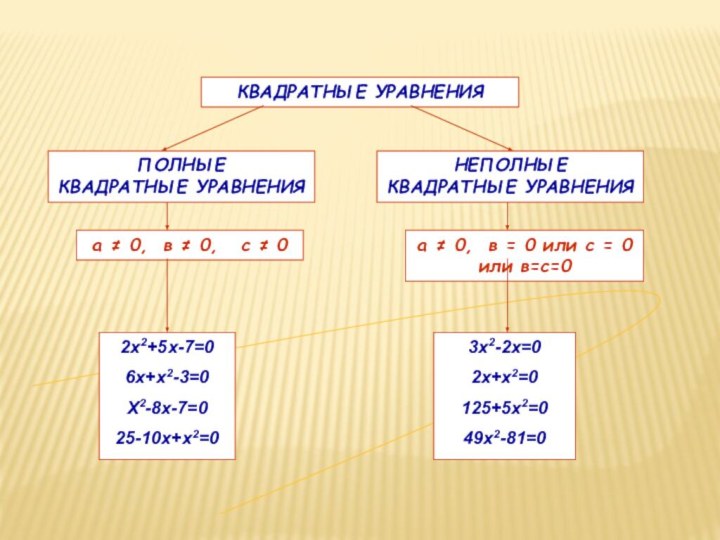
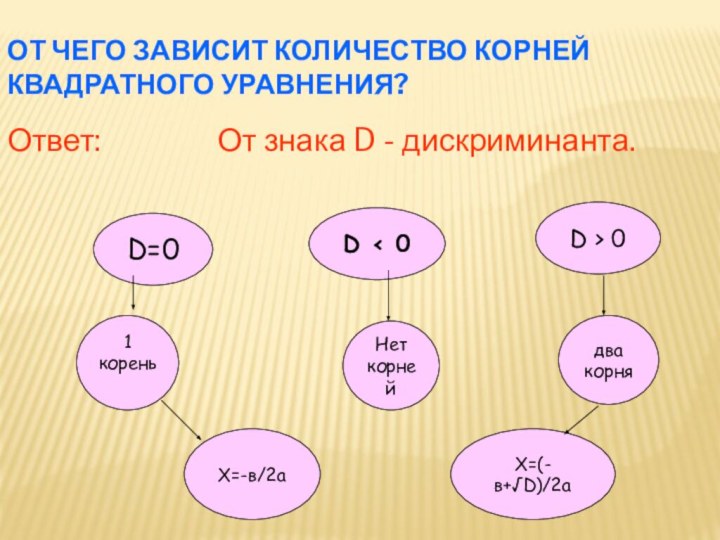
где х –переменная,

а, в и с

некоторые числа,

причем а 0
коэффициенты квадратного уравнения

a – старший коэффициент, b – второй коэффициент,

c – свободный член

ОПРЕДЕЛЕНИЕ:

Квадратным уравнением называется

0, с ≠ 0
а ≠ 0, в =

0 или с = 0 или в=с=0

2х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0

3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0

х + 4 = 0
б) 12х - х2

= 0
в) 8 + 5х2 = 0
2 вариант
а) х – 6х2 = 0
б) - х + х2 – 15 = 0
в) - 9х2 + 3 = 0

1 вариант
а) а = 6, в = -1, с = 4;
б) а = -1, в = 12, с = 0;
в) а = 5, в = 0, с = 8;
2 вариант
а) а = -6, в =1, с = 0;
б) а = 1, в =-1, с = -15;
в) а = -9, в = 0, с = 3.

Определите коэффициенты
квадратного уравнения:

правую часть уравнения.
ах2= -с
2.Деление обеих частей уравнения на а.
х2=

-с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -

Если –с/а<0 - нет решений

Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а

1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.

2 вариант:

а) 2х + 3х2= 0 а) 3х2 – 2х = 0
б) 3х2 – 243= 0 б) 125 - 5х2 = 0
в) 6х2 = -10х – 2х( 5 – 3х). в) -12х – 6х(2 – 3х) = 18х2

вариант
а) х(2+3х)=0,
х=0 или 2+3х =0,

3х = -2,
х= -2/3.
Ответ: 0 и -2/3.
б) 3х2 = 243,
х2 = 243/3,
х2 = 81,
х =-9, х= 9.
Ответ: -9 и 9.
в) 6х2 = - 10х -10х + 6х2,
6х2 +10х +10х - 6х2 =0,
20х = 0,
х=0.
Ответ: 0.

2 вариант
а) х(3х -2) =0,
х=0 или 3х-2 =0,
3х = 2,
х = 2/3.
Ответ: 0 и 2/3.
б) - 5х2 = - 125,
х2 = -125/-5,
х2 = 25,
х = - 5, х = 5.
Ответ: -5 и 5.
в) - 12х -12х +18 х2 - 18 х2 = 0,
- 24х = 0,
х = 0.
Ответ: 0.

4х2 – 4х + 1= 0
в) х2 – 2х

+3 = 0
г) 6х2 – х + 4 = 0
д) 12х - х2 = 0
е) 8 + 5х2 = 0

ж) 5х2 – 4х + 2 = 0
з) 4х2 – 3х -1= 0
и) х2 – 6х + 9= 0
к) х – 6х2 = 0
л) - х + х2 – 15 = 0
м) - 9х2 + 3 = 0

= b2- 4ac, x1,2=
Теорема Виета. Только для приведенных квадратных

уравнений

которых уравнение обращается в верное равенство

значит…
найти все его корни или установить,
что

их нет

От знака

D - дискриминанта.

1 вариант


а) 3х2 – 5х -

2 = 0
б) 4х2 – 4х + 1= 0
в) х2 – 2х +3 = 0

2 вариант


а) 5х2 – 4х + 2 = 0
б) 4х2 – 3х -1= 0
в) х2 – 6х + 9= 0

1 вариант

а) D =(-5)2 - 4*3*(-2) = 49,

2 корня;
б) D =(-4)2 - 4*4*1 = 0,
1 корень;
в) D =(-2)2 - 4*1*3 = -8,
нет корней

2 вариант

а) D =(-4)2 - 4*5*2 = -24,
нет корней;
D =(-3)2 - 4*4*(-1) = 25,
2 корня;
D =(-6)2 - 4*1*9 = 0,
1 корень

Уравнения вида x² + px +

q = 0 называют
приведёнными квадратными уравнениями.
3x² - 5x +9 = 0; -x² - 5x +9 =0; 0,8x² - 5 + 9 =0; x² - 5x + 9 = 0
Чем отличается последнее уравнение от предыдущих?
Его старший коэффициент равен 1.
Как из обычного квадратного уравнения сделать приведённое ?
Нужно обе части уравнения разделить на старший
коэффициент.


а) -x² + 31x – 6 = 0 x² - 31x + 6 = 0
б) 18 – 9x + 9x² = 0 x² - x + 2 = 0
в) -1:3 x² - 5x + 3 = 0 x² + 15x – 9 = 0

равна второму коэффициенту, взятому с противоположным знаком, а произведение

равно свободному члену.

Доказательство:
Дано приведенное квадратное уравнение. Решим его. D=p2-4q. Пусть D>0, тогда

Найдём произведение и сумму корней

n таковы, что их сумма равна –p, а произведение

равно q, то эти числа являются корнями уравнения x2+px+q=0.

Дано: m и n-некоторые числа
m+n=-p, m*n=q
Доказать: m и n-корни уравнения x2+px+q=0

Доказательство:
По условию m+n=-p, а mn=q. Значит, уравнение x2+px+q=0 можно записать в виде x2-(m+n)x+mn=0.
Подставив вместо x число m получим:
m2+(m+n)m+mn=m2-m2-mn+mn=0
Значит, число m является корнем уравнения.
Аналогично можно показать, что число n также является корнем уравнения. Что и требовалось доказать.

вариантам)

+с =0
D = k2 –ас;
если D>0,

то
х1,2 =
если D <0 , то уравнение корней не имеет.
Привести вторую запись данной формулы при условии , если в приведенном квадратном уравнении второй коэффициент чётный :

математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в)

изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
________________________________________________
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?

на поляне забавлялось – ( х/8)2 и 12 прыгали

по лианам. Составим уравнение:

( х/8)2 + 12 = х,
х2/64 + 12 – х =0, /*64
х2 - 64х + 768 = 0,
D = (-64)2-4*1*768 =4096 – 3072 = 1024 = 322, 2 корня
х= (64 -32)/2 = 16,
х= (64 + 32)/2 = 48.
Ответ: 16 или 48 обезьянок.