- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Комбинаторика. Комбинаторные конструкции (10 класс)
Содержание
- 2. **************************************************
- 3. Тема урока: Комбинаторика. Комбинаторные конструкцииКомбинаторика - это
- 4. - учебные заведения (составление расписаний) сфера общественного
- 5. Перестановка - упорядоченный набор объектовPn = n·(n-1)·(n-2)···(n-(n-1))Pn
- 6. Несколько стран в качестве символа своего государства
- 7. Устный счетВыбрать правильный ответ:
- 8. Вычислить:
- 9. Задача №2 Сколько существует анаграмм для слова КАТЕР (стр. 67)?Решение:P5 = 5!=5∙4∙3∙2∙1=120 Ответ: 120
- 10. «10 выпускников пришли в кафе отпраздновать окончание
- 11. Сколько трехзначных чисел можно составить из цифр
- 12. 1357357157137135573735357353537535357517Решение с помощью дерева возможных вариантов.
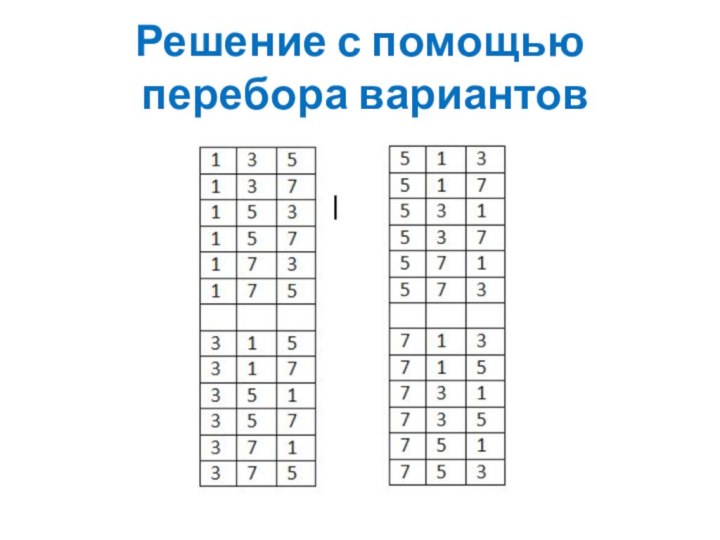
- 13. Решение с помощью перебора вариантов
- 14. Размещением из n элементов по k (k
- 15. Сколько трехзначных чисел можно составить из цифр
- 17. Задача №6Студенты 1 курса изучают 10 предметов.
- 18. Задача №7Имеется 5 цветков разного цвета. Обозначим
- 19. Если в букет входит красный цветок «a», то можно составить такие букеты:
- 26. Если в букет не входит красный цветок
- 30. Наконец, если в букет не входит ни
- 32. Сочетанием из n элементов по k называется
- 33. Имеется 5 цветков разного цвета. Обозначим их
- 34. Задача №8В магазине «Филателия» продается 8 различных
- 35. Задача № 9Из 18-ти студентов группы надо
- 36. Комбинаторные конструкции
- 37. 1 группаИз шести врачей поликлиники двух необходимо
- 38. Ответы:1 группа2 группа3 группа4 группа
- 39. Домашнее задание: Стр. 64, Занятие 1 (учебник)№
- 40. Узнали: простейшие комбинаторные конструкции, формулы для нахождения
- 41. Выберите смайлик, который соответствует Вашему настроению в
- 42. Использованные ресурсы:Математика: учебник для студ. учреждений сред.
- 43. Скачать презентацию
- 44. Похожие презентации









































Слайд 4
- учебные заведения (составление расписаний)
сфера общественного питания
(составление меню)
биология (расшифровка кода ДНК)
- химия (анализ возможных
связей между химическими элементами)- экономика (анализ вариантов купли-продажи акций)
азартные игры (подсчёт частоты выигрышей)
доставка почты (рассмотрение вариантов пересылки)
- спортивные соревнования (расчёт количества игр между участниками)
Области применения комбинаторики:
Слайд 5
Перестановка - упорядоченный набор объектов
Pn = n·(n-1)·(n-2)···(n-(n-1))
Pn =
n!
Читается: «P из n» равно «n факториал»
По определению: 0! = 1 и 1! = 1Перестановкой из n элементов называют каждое расположение этих элементов в определенном порядке
Слайд 6 Несколько стран в качестве символа своего государства решили
использовать флаг в виде трех горизонтальных полос одинаковых по
ширине, но разных по цвету: белый, синий, красный.Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
P3 = 3! = 3∙2∙1 = 6
Решение:
Ответ: 6
Слайд 9
Задача №2
Сколько существует анаграмм для слова КАТЕР
(стр. 67)?
Решение:
P5 = 5!=5∙4∙3∙2∙1=120
Ответ: 120
Слайд 10 «10 выпускников пришли в кафе отпраздновать окончание школы,
но не могли решить, как сесть, т.е. в каком
порядке. На выручку пришёл официант, который предложил сесть сегодня, как придётся, а на другой день сесть по - другому и так до тех пор, пока не наступит такой день, когда они сядут как в первый раз. Тогда их официант обещал угостить бесплатным обедом. Как вы думаете, долго ли друзьям ждать бесплатного обеда?»Задача №3
Решение:
10! = 3 628 800
Учитывая, что в году 365 дней, то это почти 9942 года.
Ответ: около 10 000 лет.
Слайд 11
Сколько трехзначных чисел можно составить из цифр 1,
3, 5 и 7, используя в записи числа каждую
из них не более одного раза? Задача №4
Слайд 14 Размещением из n элементов по k (k
любое множество, состоящее из k элементов, взятых в определенном
порядке из данных n элементов.Читается: «A из n по k»
Слайд 15 Сколько трехзначных чисел можно составить из цифр 1,
3, 5 и 7, используя в записи числа каждую
из них не более одного раза?Решение:
Ответ: 24
Слайд 16
Задача №5
Сколько имеется слов длиной 3 с неповторяющимися буквами в алфавите из 6 букв (в.4, стр. 67)?
Решение:
Ответ: 120
Слайд 17
Задача №6
Студенты 1 курса изучают 10 предметов. Сколькими
способами можно составить расписание на один день, чтобы в
нем было 4 различных предмета?Решение:
Ответ: 5040
Слайд 18
Задача №7
Имеется 5 цветков разного цвета. Обозначим их
буквами a, b, c, d, e. Требуется составить букет
из трех цветков.Слайд 26 Если в букет не входит красный цветок «а»,
а входит желтый цветок «b», то можно получить такие
букеты:Слайд 30 Наконец, если в букет не входит ни красный
цветок «а», ни желтый цветок «b», то можно составить
букет:Слайд 32 Сочетанием из n элементов по k называется любое
множество, составленное из k элементов, выбранных из данных n
элементовЧитается: «С из n по k»
Слайд 33 Имеется 5 цветков разного цвета. Обозначим их буквами
a, b, c, d, e. Требуется составить букет из
трех цветков.Решение:
Ответ: 10
Слайд 34
Задача №8
В магазине «Филателия» продается 8 различных наборов
марок, посвященных спортивной тематике. Сколькими способами можно выбрать из
них 3 набора?Решение:
Ответ: 56
Слайд 35
Задача № 9
Из 18-ти студентов группы надо выбрать
двух дежурных. Сколькими способами можно сделать этот выбор?
Решение:
Ответ: 153
Слайд 37
1 группа
Из шести врачей поликлиники двух необходимо отправить
на курсы повышения квалификации. Сколькими способами это можно сделать?
2
группаСколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
3 группа
В группе 7 студентов успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде по предмету?
4 группа
Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?
Слайд 39
Домашнее задание:
Стр. 64, Занятие 1 (учебник)
№ 4.37
(стр. 80, задачник)
№ 4.44 (стр. 80, задачник)
Дополнительно:
В группе учатся
12 мальчиков и 10 девочек. Для уборки территории нужно выделить 4 мальчиков и 3 девочек. Сколькими способами это можно сделать?
Слайд 40
Узнали:
простейшие комбинаторные конструкции, формулы для нахождения простейших
комбинаций (перестановок, размещений и сочетаний).
Научились:
различать простейшие комбинаторные конструкции;
вычислять
количество перестановок, размещений и сочетаний;решать простейшие комбинаторные задачи.
Подведем итоги
Слайд 41 Выберите смайлик, который соответствует Вашему настроению в конце
урока
Спасибо за урок!
Мне было очень трудно. Я ничего
не
понял.Мне всё удалось!
Мне не все удалось, придется дома подольше посидеть…
Слайд 42
Использованные ресурсы:
Математика: учебник для студ. учреждений сред. проф.
образования / М.И. Башмаков. - М.: Издательский центр «Академия»,
2014;Математика. Задачник: учебное пособие для студ. учреждений сред. проф. образования / М.И. Башмаков. - М.: Издательский центр «Академия», 2014;
Презентация учителя математики МБОУ СОШ №2 г. Горячий ключ Л.Г. Миносян «Комбинаторика. Комбинаторные задачи»;
Алгебра: элементы статистики и теории вероятностей: учеб. пособие для учащихся 7—9 кл. общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк; под ред. С. А. Теляковского.— М.: Просвещение, 2005.