- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему: Алгебраические уравнения четвёртой степени
Содержание
- 3. Так как f(x) является многочленом чётной степени,
- 4. Решение уравнений четвертой степени можно проводить по
- 5. Комплексные числа
- 6. Решение двучленного уравнения четвертой степениЭтот тип уравнений
- 7. Решение возвратного уравнения четвертой степени 2. Проведем
- 8. 1. Это уравнение в силу симметрии коэффициентов
- 9. Решение биквадратного уравнения
- 10. Решение уравнений четвертой степени по методу Феррари
- 11. Метод Горнера
- 12. В верхней строке выставляются коэффициенты исходного многочлена.
- 13. Но это еще не конец. Можно попробовать
- 15. Повторим основные методы1. Решение двучленного уравнения четвертой
- 16. Скачать презентацию
- 17. Похожие презентации
Так как f(x) является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a>0, то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция

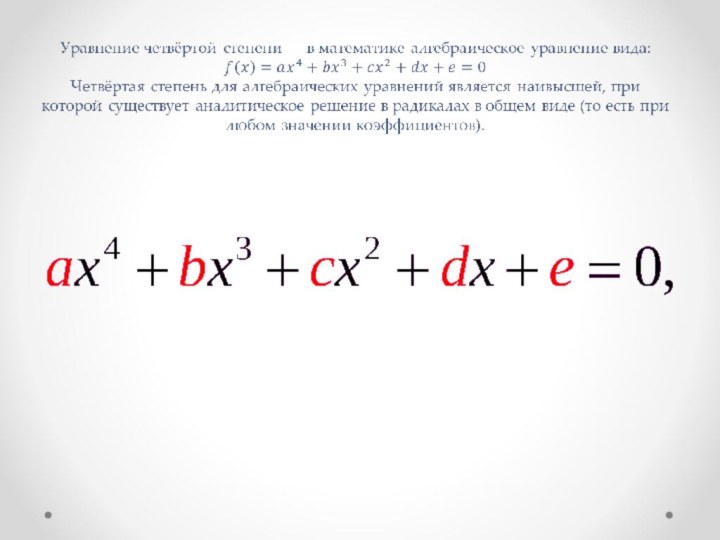














Слайд 4 Решение уравнений четвертой степени можно проводить по общей
схеме решения уравнений высших степеней. Однако, есть несколько специфических
видов таких уравнений – двучленное, биквадратное и возвратное. На них подробно остановимся. Метод Феррари позволяет свести решение к кубическому уравнению. Иногда применение искусственных приемов разложения многочлена на множители быстро приводит к результату.
Слайд 6
Решение двучленного уравнения четвертой степени
Этот тип уравнений четвертой
степени является простейшим, само уравнение имеет вид формула. Решается
с использованием формул сокращенного умножения.
Слайд 7
Решение возвратного уравнения четвертой степени
2. Проведем замену переменных :
Таким образом, возвратное уравнение четвертой степени сводится к квадратному
уравнению.Слайд 8 1. Это уравнение в силу симметрии коэффициентов является
возвратным. Разделим на обе части уравнения (х=0 корнем не является, поэтому
деление не приведет к потере этого корня).2. Проведем группировку:
3. Сделаем замену переменной:
4. Возвращаемся к замене и решаем два квадратных уравнения
Таким образом мы находим 4 комплексных корня возвратного уравнения четвёртой степени
Слайд 10
Решение уравнений четвертой степени по методу Феррари
Имеем А=3, В=3,
С=-1, D=-6. Решим этот пример по методу Феррари.
1. Составляем
и решаем кубическое уравнение
Слайд 12 В верхней строке выставляются коэффициенты исходного многочлена. В
первой ячейке второй строки ставится найденный нами корень 2. Во второй
строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки.
Слайд 13 Но это еще не конец. Можно попробовать разложить
таким же способом многочлен 2x3 + 9x2 + 7x - 6.
Опять ищем
корень среди делителей свободного члена. Делителями числа -6являются ±1, ±2, ±3, ±6.1: 2 + 9 + 7 - 6 = 12 ⇒ число 1 не является корнем многочлена
-1: -2 + 9 - 7 - 6 = -6 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 - 6 = 60 ⇒ число 2 не является корнем многочлена
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) - 6 = 0 ⇒ число -2 является корнем многочлена
Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки: