Слайд 2
Kas sukūrė Pitagoro teoremą?
Pitagoras Samietis(582 m.
pr. m.
e. – 496 m. pr. m. e.)
– jonėnų
mistikas, filosofas
ir matematikas, religinio-
mokslinio pitagorininkų
sąjūdžio įkūrėjas. Jo
vardas tradiciškai siejamas
su Pitagoro teoremos
suformulavimu.
Слайд 3
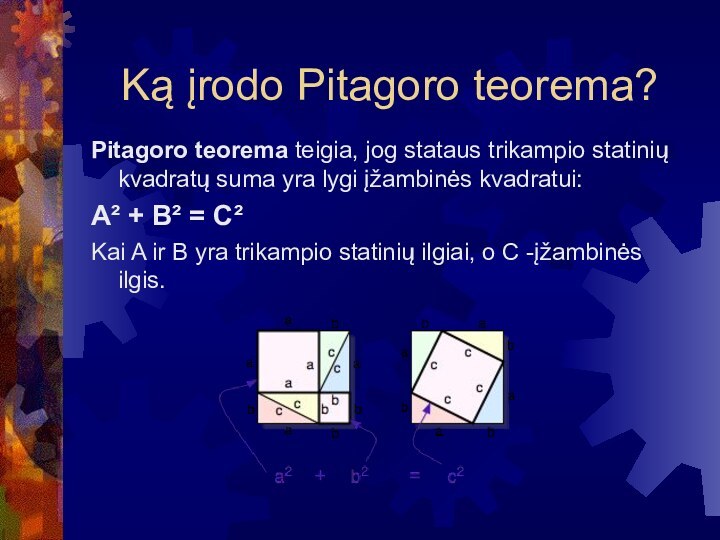
Ką įrodo Pitagoro teorema?
Pitagoro teorema teigia, jog stataus
trikampio statinių kvadratų suma yra lygi įžambinės kvadratui:
A² +
B² = C²
Kai A ir B yra trikampio statinių ilgiai, o C -įžambinės ilgis.
Слайд 4
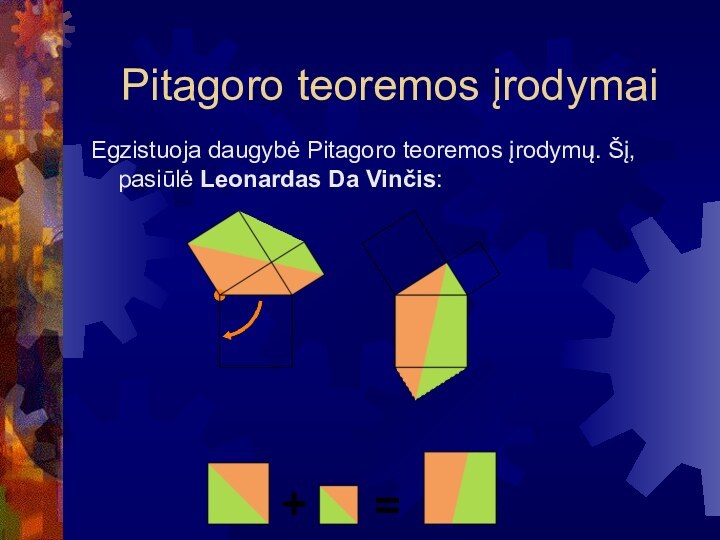
Pitagoro teoremos įrodymai
Egzistuoja daugybė Pitagoro teoremos įrodymų. Šį,
pasiūlė Leonardas Da Vinčis:
Слайд 5
Paprasčiausias įrodymas
Šis įrodymas nereikalauja ploto sąvokos ir išvedamas
vien tik iš aksiomų.
Paimkime statųjį trikampį ABC su
stačiu kampu C, iš kurio nuleiskime aukštinę CH į įžambinę AB. Trikampis ACH yra panašus į trikampį ABC pagal du kampus. Pagal tai ir trikampis CBH panašus į trikampį ABC.
Tad:
a/c = |HB| / a;
b/c = |AH| / b
Iš čia gauname
a2 = c*|HB|
b2 = c*|AH|
Sudėję abi lygtis gauname:
a2 + b2 = c*(|HB|+|AH|) = c2
Слайд 6
Truputėlis istorijos
Teorema pavadinta graikų matematiko Pitagoro (569-475 m.
pr.m.e.) vardu, tačiau ji jau anksčiau buvo žinoma babiloniečiams,
indams, kinams. O seniausias išlikęs teoremos įrodymas Senovės Graikijoje yra Euklido „Pradmenyse”, o jos priskyrimas Pitagorui tėra tik rašiniuose, parašytuose praėjus 5 a. po Pitagoro mirties.
M. Kantoras mano, kad Pitagoro teorema kraštinėms 3, 4 ir 5 buvo žinoma jau senovės Egipte apie 2000 m. pr.m.e. (pagal Berlyno muziejuje esantį papirusą nr. 6619, datuojamą 2000-1786 m. pr.m.e.). Kiek daugiau žinoma apie teoremą Babilone. „Plimpton 322″ molio lentelėje, datuojamoje maždaug 1790-1750 m. pr.m.e., t.y. valdant Hamurabiui, tekste pateikiama keletas užrašų, artimų Pitagoro trejetams.
Слайд 7
Truputėlis istorijos(2)
Indijos „Baudhayana Sulba sutra”, datuojama kažkur 8-2
a. pr.m.e., pateikia Pitagoro trejetų sąrašą, teoremos formuluotę ir
geometrinį jos įrodymą lygiašoniams trikampiams. „Apastamba Sulba sutra” (apie 600 m. pr.m.e.) pateikia skaitinį teoremos įrodymą panaudojant plotų paskaičiavimus. Gali būti, kad remiamasi ankstesnėmis tradicijomis.
Žinoma anksčiau, tačiau išlikusi 1 a. pr.m.e. „Čou Pei Suan Čing ” pateikia Pitagoro teoremą su piešiniu (Kinijoje vadintoje Gougu teorema) trikampiui su kraštinėmis, lygiomis 3, 4 ir 5. Hanų dinastijos laikotarpiu (202 m. pr.m.e. - 220 m.) Pitagoro trejetas pateikiamas „Devyniuose matematikos skyriuose”, paminint ir stačiuosius trikampius.
Слайд 8
Atvirkštinė Pitagoro teorema
Jei trikampio dviejų kraštinių ilgių kvadratų
suma lygi trečiosios kraštinės ilgio kvadratui, tai tas trikampis
yra status.
Слайд 9
Statinis prieš 30° kampą
Jei stačiojo trikampio vienas kampas
lygus 30°, tai prieš jį esantis statinis lygus pusei
įžambinės.
Jei trikampio vienas kampas yra C=90 laipsniu, o kitas kampas yra A=30 laipsniu, tai kraštinė a esanti priešais 30 laipsnių kampą yra dvigubai trumpesnė už ižambinę C, t. y. A=C/2. Pavyzdžiui, jei AC=1, tai AB=0,5. O kraštinė, esanti priešais kampą a.
Слайд 10
Uždaviniai(1)
Trikampio dviejų trumpesniųjų kraštinių ilgiai decimetrais yra:
6
ir 8; a²=6² + 8² = 100; a=10dm
10 ir
24; a²=10² + 24² = 676; a=26dm
8 ir 15; a²=8² + 15² = 289; a=17dm
9 ir 40; a²=9² + 40² = 1681; a=41dm
Kokie galėtų būti trikampio trečiosios kraštinės ilgiai sveikaisiais decimetrų skaičiais?
Слайд 11
Uždaviniai(2)
Trikampio ABC dviejų kraštinių ilgiai yra:
BC = 42mm;
CA = 40mm
AB² = BC² + CA²; AB² = 42²
+ 40² = 3364; AB = 58mm
AB = 7.8cm; BC = 7.2cm
CA² = AB² - BC²; CA² = 7.8² - 7.2² = 9; CA = 3cm
BC = 15.4cm; CA = 7.2cm
AB² = BC² + CA²; AB² = 15.4² + 7.2² = 289; AB = 17cm
Koks turėtų būti trikampio trečiosios kraštinės ilgis, kad trikampis būtų status, o AB būtų įžambinė?
Слайд 12
Uždaviniai(3)
Apskaičiuokite stačiojo trikampio įžambinės c ilgį, kai žinomi
jo statinių a ir b centimetrais.
a = 9;
b = 12; c² = a² + b² = 225; c = 15cm
a = 5; b = 12; c² = a² + b² = 169; c = 13cm
a = 15; b = 8; c² = a² + b² = 289; c = 17cm
a = 16; b = 30; c² = a² + b² = 1156; c = 34cm
a = 2.4; b = 0.7; c² = a² + b² = 6.25; c = 2.5cm
a = 6; b = 1.75 c² = a² + b² = 39.0625; c = 6.25cm
Слайд 13
Uždaviniai(4)
Apskaičiuokite stačiojo trikampio statinio b ilgį, kai žinomas
įžambinės c ilgis milimetrais.
c = 17; a =
8; b² = c² - a² = 225; b = 15mm
c = 25; a = 24; b² = c² - a² = 49; b = 7mm
c = 29; a = 21; b² = c² - a² = 400; b = 20mm
c = 3.4; a = 3 b² = c² - a² = 2.56; b = 1.6mm
Слайд 14
Uždaviniai(5)
Stačiojo trikampio statiniai yra a ir b, o
įžambinė yra c. Apskaičiuokite trikampio nežinomos kraštinės ilgį, kai:
a = 5dm; b = 12dm; c² = a² + b² = 169; c = 13dm
a = 4dm; c = 4.1dm; b² = c² - a² = 0.81; b = 0.9dm
b = 2m; a = 1.5m; c² = a² + b² = 6.25; c = 2.5m
b = 10cm; c = 50.5cm a² = c² - b² = 2450.25; b = 49.5cm
Слайд 15
Uždaviniai(6)
Nustatykite ar trikampis yra status, jei jo kraštinių
ilgis yra:
45, 28, 53 Taip, nes 45² + 28²
= 53²
22, 20, 29 Ne, nes 22² + 20² nėra 29²
10, 24, 28 Ne, nes 10² + 24² nėra 28²
33, 56, 65 Taip, nes 33² + 56² = 65²
Слайд 16
Uždaviniai(7)
Trikampio įžambinės ilgis yra 26m, o trumpesniojo statinio
– 10m. Raskite kito trikampio statinio ilgį.
AC = 26m;
CB = 10m;
AB = ?
AB² = AC² - CA²
AB² = 26² - 10² = 676 – 100 = 576
AB = 24m Ats.: AB = 24m
Слайд 17
Uždaviniai(8)
Trikampio įžambinės AC ilgis yra 24m.
yra 30°. Raskite statinio AB ilgį metrais.
AC = 24m,
AB = ?
AB = AC : 2
AB = 24 : 2 = 12m
Ats.: AB = 12m
Слайд 18
Uždaviniai(9)
Nustatykite ar trikampis yra status, jei jo kraštinių
ilgiai centimetrais yra:
24, 32, 40 Taip, nes 24² +
32² = 40²
14, 48, 50 Taip, nes 14² + 48² = 50²
7, 24, 30 Ne, nes 7² + 24² nėra 30²
13, 84, 85 Taip, nes 13² + 84² = 85²