- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Семинар для педагогов начальных классов Трудности при обучении математике младших школьников консультация (2, 3, 4 класс) по теме
Содержание
- 2. «ЗЕРКАЛЬНОЕ» НАПИСАНИЕ ЦИФРНедостаточность процессов зрительного анализа –
- 3. ЗАТРУДНЕНИЯ В СЧЁТЕ, ОТСУТСТВИЕ УСТОЙЧИВЫХ НАВЫКОВ СЧЁТАНе
- 4. ТРУДНОСТИ ПРИ ВЫПОЛНЕНИИ СЧЁТНЫХ ОПЕРАЦИЙ С ПЕРЕХОДОМ
- 5. ОШИБКИ ПРИ РЕШЕНИИ ПРИМЕРОВ, В ТОМ ЧИСЛЕ
- 6. ТРУДНОСТИ В НАЗЫВАНИИ КОМПОНЕНТОВ ПРИ ВЫПОЛНЕНИИ АРИФМЕТИЧЕСКИХ
- 7. ЗАТРУДНЕНИЯ ПРИ ПЕРЕВОДЕ ИЗ СЛОВЕСНОЙ ФОРМЫ В
- 8. ОШИБКИ В ЗАПИСЯХ ПРИ ИЗУЧЕНИИ ДЕЙСТВИЙ С
- 9. ОШИБКИ ПРИ ЗАПИСИ СОСТАВА ЧИСЕЛНеотдифференцированность понятий «число»
- 10. ТРУДНОСТИ В ОБОЗНАЧЕНИИ ЧИСЛОМ МНОЖЕСТВНе сформировано умение
- 11. ТРУДНОСТИ РЕШЕНИЯ ЗАДАЧ И ПРИМЕРОВ С БУКВЕННЫМИ
- 12. НЕСПОСОБНОСТЬ РЕШАТЬ ЗАДАЧИ НЕСКОЛЬКИМИ СПОСОБАМИНедостаточная гибкость мыслительной
- 13. НЕУМЕНИЕ РЕШАТЬ ЗАДАЧИНедостаточность процессов анализа и анализа
- 14. САМБУРСКАЯ А.А. - АВТОР МЕТОДИКИ ОБУЧЕНИЯ ДЕТЕЙ
- 15. Формулируем Главное Правило:Учим ребенка не тому «где какая
- 16. Прежде чем выходить за пределы двадцатка вы
- 17. При решении математических и музыкальных задач наш
- 18. Скачать презентацию
- 19. Похожие презентации
«ЗЕРКАЛЬНОЕ» НАПИСАНИЕ ЦИФРНедостаточность процессов зрительного анализа – з.3,4,5Недостаточность анализа пространственных отношений – з.31,32Отсутствие прочной связи между зрительным и двигательным образами цифр – з.30

















Слайд 2
«ЗЕРКАЛЬНОЕ» НАПИСАНИЕ ЦИФР
Недостаточность процессов зрительного анализа – з.3,4,5
Недостаточность
анализа пространственных отношений – з.31,32
и двигательным образами цифр – з.30
Слайд 3
ЗАТРУДНЕНИЯ В СЧЁТЕ, ОТСУТСТВИЕ УСТОЙЧИВЫХ НАВЫКОВ СЧЁТА
Не сформирован
переход из конкретного плана действий в абстрактный – з.47,
81Несформированность понятий «больше» и «меньше» – з.86
Недостаточное развитие пространственных отношений – з.31,32
Сниженный уровень интеллектуальной деятельности – повысить качество мыслительной деятельности путём использования развивающих заданий на анализ, синтез, обобщение, классификацию и др.
Слайд 4 ТРУДНОСТИ ПРИ ВЫПОЛНЕНИИ СЧЁТНЫХ ОПЕРАЦИЙ С ПЕРЕХОДОМ ЧЕРЕЗ
ДЕСЯТОК
Недостаточное развитие анализа пространственных отношений – з.31,32
Несформированность мыслительной операции
«анализ через синтез» – з.46, 88, 92Слайд 5 ОШИБКИ ПРИ РЕШЕНИИ ПРИМЕРОВ, В ТОМ ЧИСЛЕ С
ДЕЙСТВИЯМИ РАЗНЫХ СТУПЕНЕЙ
Несформированность мыслительной операции «анализ через синтез» –
з.46, 88, 92Недостаточное развитие анализа пространственных отношений – з.31,32
Низкий уровень сформированности внутреннего плана действия – з.82,83
Недостатки в развитии процессов произвольного внимания – з.2
Не сформирована однонаправленность считывания слева направо – з.6
Слайд 6
ТРУДНОСТИ В НАЗЫВАНИИ КОМПОНЕНТОВ ПРИ ВЫПОЛНЕНИИ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Недостаточное
развитие смысловой памяти –з.16,18,52
Недостаточная отдифференцированность понятий «сложение», «вычитание», «умножение»,
«деление» - з.89,90Слайд 7 ЗАТРУДНЕНИЯ ПРИ ПЕРЕВОДЕ ИЗ СЛОВЕСНОЙ ФОРМЫ В ЦИФРОВУЮ
И НАОБОРОТ
Несформированность прочных ассоциативных связей между словесным обозначением и
графической формой чисел – надо записывать цифровые данные словами и наоборотНезнание состава чисел – з.84
Слайд 8 ОШИБКИ В ЗАПИСЯХ ПРИ ИЗУЧЕНИИ ДЕЙСТВИЙ С ДРОБЯМИ,
ПРИ ВОЗВЕДЕНИИ ЧИСЛА В СТЕПЕНЬ
Недостаточность анализа пространственных отношений –
з.31,32Незнание соответствующего учебного материала – ликвидировать пробелы в знаниях
Слайд 9
ОШИБКИ ПРИ ЗАПИСИ СОСТАВА ЧИСЕЛ
Неотдифференцированность понятий «число» и
«цифра» – з.91
Неусвоенность позиционного принципа построения многозначных чисел –
з.84Недостаточность анализа пространственных отношений – з.31,32
Недостаточность процессов зрительного анализа – з.3,4,5
Слайд 10
ТРУДНОСТИ В ОБОЗНАЧЕНИИ ЧИСЛОМ МНОЖЕСТВ
Не сформировано умение перехода
из конкретного плана в абстрактный – з.47,81
Недостаточность анализа пространственных
отношений – з.31,32Не усвоено понятие числа – з.50, 51
Слайд 11
ТРУДНОСТИ РЕШЕНИЯ ЗАДАЧ И ПРИМЕРОВ С БУКВЕННЫМИ ОБОЗНАЧЕНИЯМИ
Недостаточность
мыслительной операции абстрагирования – з.47, 81
Недостаточное развитие процессов обобщения
– з.17,19, 54, 79,101
Слайд 12
НЕСПОСОБНОСТЬ РЕШАТЬ ЗАДАЧИ НЕСКОЛЬКИМИ СПОСОБАМИ
Недостаточная гибкость мыслительной деятельности
– з.15, 85, 95
Недостаточное развитие операции «анализ через синтез»
– з.62
Слайд 13
НЕУМЕНИЕ РЕШАТЬ ЗАДАЧИ
Недостаточность процессов анализа и анализа через
синтез – з.46, 85, 92,94
Синкретичность мышления – з.95
Конкретность мышления
– з.96Несформированность мыслительной операции обобщения – з.17,19,54,79
Недостатки в развитии процессов памяти –з.13,14
Недостатки в развитии произвольного внимания –з.2
Шаблонность мышления – з.15,85
Слайд 14 САМБУРСКАЯ А.А. - АВТОР МЕТОДИКИ ОБУЧЕНИЯ ДЕТЕЙ ЧТЕНИЮ,
ПИСЬМУ И МАТЕМАТИКЕ НА ОСНОВЕ МУЗЫКАЛЬНОЙ ДЕЯТЕЛЬНОСТИ
По данным
психофизиологов (Т.М.Марютина, О.Ю.Ермолаев, А.Л.Сиротюк и др.), в период формирования мозга (до 7-9 лет) вклад правого полушария в обеспечение психологического функционирования превышает вклад левого полушария, познавательная деятельность детей в возрасте до 7 лет имеет непосредственный, целостный и образный характер.
Слайд 15
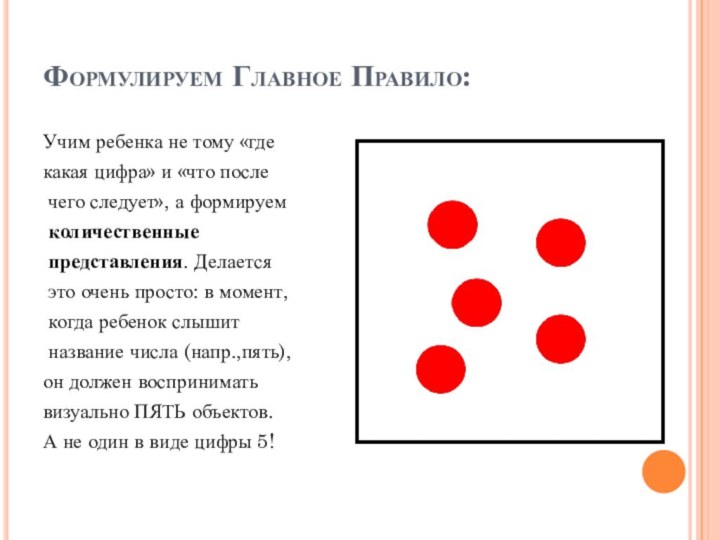
Формулируем Главное Правило:
Учим ребенка не тому «где
какая цифра»
и «что после
чего следует», а формируем
количественные
представления. Делается
это очень просто: в момент,когда ребенок слышит
название числа (напр.,пять),
он должен воспринимать
визуально ПЯТЬ объектов.
А не один в виде цифры 5!
Слайд 16
Прежде чем выходить за пределы двадцатка вы должны
быть уверены, что ребенок:
1. считает до 20 и обратно
2.
быстро определяет количество предметов в пределах 10 (грибы у вас в лесу могут расти по пять штук, по семь и т.д.)3. понимает где предметов больше, а где меньше, где одинаковое количество (можно раскладывать предметы в два ряда)
4. понимает состав числа, т.е. может разложить число на слагаемые (у нас 5 яблок, пробуем разложить эти яблоки на две тарелки разными способами).
5. понимает значение слов "добавить" "прибавить", "убрать", "отнять", "равно". Вот такие задачки на состав числа: Для супа Маше нужны четыре картофелины, две у нее уже есть. Сколько ей не хватает картофелин, чтобы стало 4? Сколько нужно добавить? Обязательно все эти действия иллюстрируете.
Слайд 17 При решении математических и музыкальных задач наш мозг
производит довольно схожие операции
После знакомства с
"двадцаткой" отрабатываем
вычислительные навыки,
состав
числа, даем понятиецифрам, и только потом
переходим в сотню –
причем, я делаю это на
таблице (по типу таблицы
стосчета Зайцева) или
числовой прямой.







![Презентация по обучению грамоте. Буквы П, п. Звуки [п], [п,]](/img/tmb/7/658987/d6e546f14c077d86d6470722c0264173-210x.jpg)





















