Презентация на тему Суждение

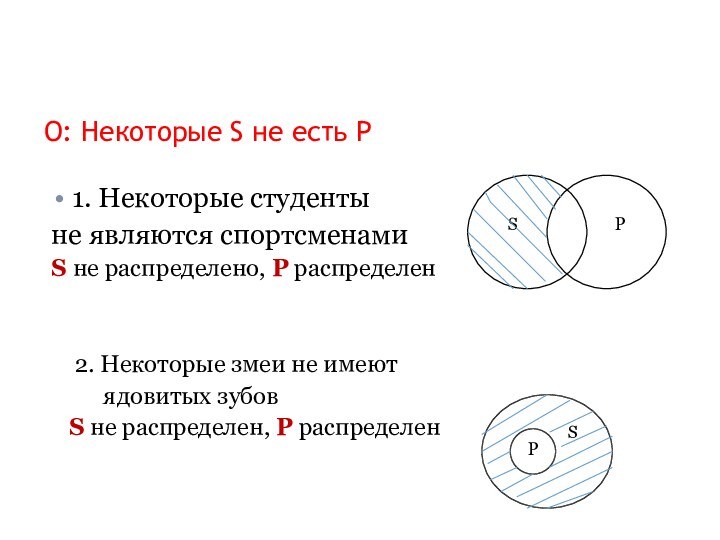
которой нечто утверждается или отрицается о существовании предмета, связях

между предметом и свойством или об отношениях между предметами.
Суждение может быть истинным или ложным.
Не всякое предложение является суждением. Не являются суждением вопросительные и побудительные суждения «Закрой дверь», «Кто сегодня дежурный?».
По составу суждения делятся на простые и сложные.

состоит из следующих структурных элементов: субъекта, предиката, связки, квантора.
Субъект

суждения – это то, о чем говорится в данном суждении. Обозначается буквой "S" (от лат. subjektum - лежащий в основе).
Предикат суждения – это то, что говорится о субъекте суждения. Обозначается буквой "Р"(от лат. слова predikatum - сказанный).

установившиеся в суждении между субъектом и предикатом. Обозначается знаком

"тире" (-) и может подразумеваться или быть выражена одним словом или группой слов: "есть", "суть", "не является", "имеется" и т.п.
По качеству связки суждения бывают утвердительные (связка «есть») или отрицательными (связка «не есть»)

указывает, относится ли суждение ко всему или к части

объема понятия, выражающего субъект ("все", "некоторые", "многие", "ни один" и т.п.). «S есть Р», «S не есть Р»

Пример: «Все люди смертны», «Ни один злой человек не бывает счастлив»

есть(не есть) Р, общие: Все S есть (не есть) Р, частные:

Некоторые S есть (не есть)Р Единичные и общие суждения в процессе рассуждения ведут себя одинаково, так как S берется в этих суждениях в полном объеме. Поэтому единичные утвердительные и общеутвердительные суждения получили обозначение латинской буквой А. Единичные отрицательные и общеотрицательные суждения обозначаются латинской буквой Е

Общеотрицательные E – все S не есть Р
Частноутвердительные I – некоторые

S есть Р
Частноотрицательные О – некоторые S не есть Р

считается тогда, когда его объем полностью включен в объем

другого термина, либо полностью исключен из объема другого термина.
Термин считается нераспределенным, если его объем только частично включается в объем другого термина либо частично исключается из него.
Рассмотрим все четыре типа суждений: А,Е,I,О:
А: «Все S есть Р»
Первый вариант: Все птицы имеют крылья
S распределен, Р не распределен
Второй вариант: Все квадраты –
прямоугольные ромбы

спортсмены
S и Р - оба не распределены

по объемам
2. Некоторые писатели – драматурги
S не распределен, Р – распределен



Е: Ни одно S не есть Р
Оба термина S и Р распределены
относительно друг друга

не являются спортсменами
S не распределено, Р распределен


2.

Некоторые змеи не имеют
ядовитых зубов
S не распределен, Р распределен

простых, соединенных логической связкой.

Виды связок:
 - конъюнкция (грамматические

союзы «и», «а», «но», «да», точка, запятая, двоеточие, точка с запятой, дефис.);
V – слабая дизъюнкция (грамматические союзы «или…или», «либо … либо» в значении «и то, и другое вместе»);
V – строгая дизъюнкция (грамматические союзы «или … или», «либо … либо» в значении «что-то одно из двух»);
 - импликация (грамматические союзы «если …, то», «когда …, тогда», «следовательно», «значит»);
 (↔) - эквиваленция (грамматические союзы «если и только если …, то», «тогда и только тогда …, когда»).

.

делятся на следующие виды:
соединительные (конъюнктивные);
разделительные (дизъюнктивные). Существует два вида

разделительных (дизъюнктивных) суждений: а) исключающе-разделительные (используется строгая дизъюнкция); б) соединительно-разделительные (используется слабая дизъюнкция);
условные (импликативные);
эквивалентные.

качестве элементов простые суждения и обозначить их переменными;
расставить между

переменными логические связки, соответствующие союзам.

Пример: Обоснуйте правильность вывода с помощью таблицы истинности: Если игроки « Динамо» выиграют предстоящий матч, а команда «Спартак» потерпит поражение, то команда «Торпедо» займет призовое место. Но команда «Торпедо» не заняла призового места. Значит, либо игроки «Динамо» проиграли матч, либо команда «Спартак» не потерпела поражение.

игроки « Динамо» выиграют предстоящий матч
В - команда «Спартак»

потерпит поражение
С - команда «Торпедо» займет призовое место
Не-С - команда «Торпедо» не заняла призового места
Не-А - игроки «Динамо» проиграли матч
Не-В - команда «Спартак» не потерпела поражение

не- С)  (не-А V не-В)
Количество строк в таблице

истинности определяется по формуле 2, где n – количество переменных.
Количество столбиков равно количеству переменных плюс количество подформул, входящих в исходную формулу.

(половина «И», половина «Л»)
* 2 столбик (четверть «И» ,

четверть «Л», четверть «И» , четверть «Л»)
* и т.п.
* последний столбик всегда содержит чередование «И» и «Л».
для формулы (((А  В)  С)  не-С)  (не-А Vне- В)
* количество строк равно 2 = 8
* чередование комбинаций «И» и «Л» следующее:
1 столбик - 4 раз подряд «И», 4 раз подряд «Л».
2 столбик - 2 раза подряд «И», 2 раза подряд «Л», 2 раза подряд «И», 2 раза подряд «Л».
3 столбик - содержит чередование «И» и «Л».
количество столбиков равно 3 (3 переменные) + 5 (5 подформул исходной формулы) = 8.
(А  В)
(А  В)  С
((А  В)  С)  не-С
(не-А V не-В)
(((А  В)  С)  не-С)  (не-А V не-В)
* - (((А  В)  С)  не-С)  (не-А Vне- В)

- истинная), поэтому вывод по этой формуле является логически

неправильным, не убедительным.

«логического квадрата»