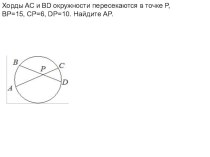
Презентация на тему по геометрии на тему Геометрические фигуры в нашей жизни ученицы 9 класса

расчёты производили свыше тысячи лет назад. Древние люди составляли

на стенах пещер орнаменты из треугольников, ромбов, кругов. Со временем человек научился использовать свойства фигур в практической жизни. Геометрия в быту. Стены, пол и потолок являются прямоугольниками. Многие вещи напоминают окружность, например, обруч, кольцо, тарелка. Арбуз, глобус, мячи - похожи на геометрический шар. Предметов, имеющих форму цилиндра и конуса в окружающем нас мире очень много: трубы, кастрюли, бочки, стаканы, консервные банки.

фигуры, поверхности, можно встретить только в книгах учёных математиков.

Однако, стоит посмотреть вокруг, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Оказывается их очень много. Просто мы их не всегда замечаем. Множество геометрических фигур окружает нас например: круг, овал, квадрат, прямоугольник, треугольник и многие другие.

за природой. Люди – творческие создания: большая часть окружающих

нас объектов приняла геометрические очертания, которые из которых не существуют в природе.
Геометрия присутствует практически во всех сферах нашей жизни: нас окружают круглые, квадратные, прямоугольные, треугольные, сферические, кубические, цилиндрические, конические и другие объекты. Обычно мы не задумываемся о том, почему объекты имеют ту или иную форму, а ее выбор далеко не случаен.
Одна из самых распространенных форм – это окружность и то, что ею ограничено, то есть круг. Вы, наверное, не задумывались, почему трубы – круглые в сечении.

– это замкнутая дуга с постоянной шириной. По этой

причине, например, люки не проваливаются вниз, что приводило бы к несчастным случаям, а будь они квадратными и прямоугольными, это стало бы неизбежным.
Еще одно свойство окружности: из всех замкнутых кривых заданной длины круг покрывает наибольшую площадь. Это объясняет тот факт, что природа часто использует круг и его объемный эквивалент – сферу.  Природа всегда останавливает выбор на самых стабильных формах, минимально расходующих энергию.

используются самые разные геометрические формы. Многие жилые дома украшаются

колоннами. Геометрические фигуры различной формы можно увидеть в постройке соборов и конструкциях мостов. Геометрия транспорта. По улице движутся автомобили, трамваи, троллейбусы, велосипеды. Их колёса с геометрической точки зрения – круги. Сложную форму имеет корпус подводной лодки. Корпус космического спутника состоит из цилиндров. Сложную форму имеют и детали машин – гайки, винты, зубчатые колёса

много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники,

созданные природой. Кристаллы горного хрусталя напоминают отточенный карандаш. Кристалл соли имеет форму куба. А снежинки – это одна из самых красивых геометрических фигур. Обычная горошина, капельки росы – имеют форму шара.

геометрию не изучали, но природа наделила их талантом строить

себе дома в форме геометрических тел. Многие птицы строят гнёзда в форме пол шара. Но самые искусные геометры – пчёлы. Они строят соты из шестиугольников. Одним из этапов нашей работы был творческий. Мы подготовили выставку поделок, в основе которых лежат геометрические фигуры. Из всего изученного мы сделали вывод: геометрия нужна не только для того, чтобы называть части строений или формы окружающего нас мира, с помощью геометрии мы можем решить многие задачи, ответить на многие вопросы.

дети не мыслят своей жизни без компьютера. Математика –

наука для глаз, а не для ушей. Объяснение нового материала. Трапеция. Определение. Типы трапеций. Средняя линия трапеции. Свойства равнобедренной трапеции. В равнобедренной трапеции диагонали равны. Признаки равнобедренной трапеции. Задачи на готовых чертежах. Признаки равенства треугольников. Первый признак равенства треугольников. Второй признак равенства треугольников. Использование ИКТ. Ученик вовлечен в активные действия в процессе обучения.

стороны равны и параллельны. Если у четырехугольника противоположные стороны

попарно равны, то четырехугольник – параллелограмм. Диагонали параллелограмма точкой пересечения делятся пополам. В параллелограмме противоположные стороны и противоположные углы равны.

Свойства ромба. Признаки. Периметр. Формула площади. Ромб в жизни.

Сказка про ромб. Интересные факты. Ромб, в котором проведены диагонали.

Фракталы в природе. Понятие "фрактал". Роль фракталов в машинной

графике сегодня достаточно велика. Одним из основных свойств фракталов является самоподобие. Геометрические фракталы. Треугольник Серпинского. Алгебраические фракталы. Вторая большая группа фракталов - алгебраические. Методов получения алгебраических фракталов несколько. Множство Мандельброта. Обратимся к классике - множству Мандельброта. Все множество Мандельброта в полной красе у нас перед глазами. Множество Жюлиа. Галерея фракталов.

вокруг нас. Подобные треугольники. Подобие плоских фигур. Если изменить

все размеры плоской фигуры в одно и то же число раз ( отношение подобия, то старая и новая фигуры называются подобными. Подобие в нашей жизни. Вокруг нас великое множество подобных фигур. Подобие нас окружает. Вот некоторые примеры из нашей жизни. Игрушки. Растения. Животные. Использовались материалы Интернета.