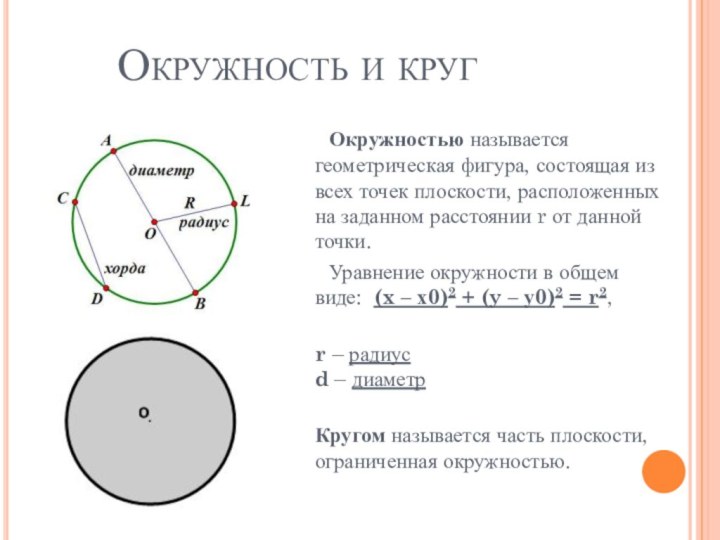
из всех точек плоскости, расположенных на заданном расстоянии r
от данной точки.Уравнение окружности в общем виде: (x – х0)2 + (y – у0)2 = r2,
r – радиус d – диаметр
Кругом называется часть плоскости, ограниченная окружностью.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

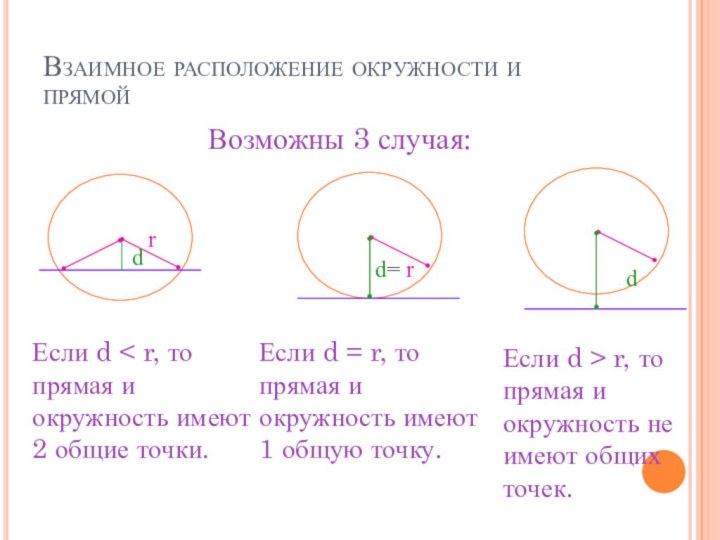







Если d > r, то прямая и окружность не имеют общих точек.
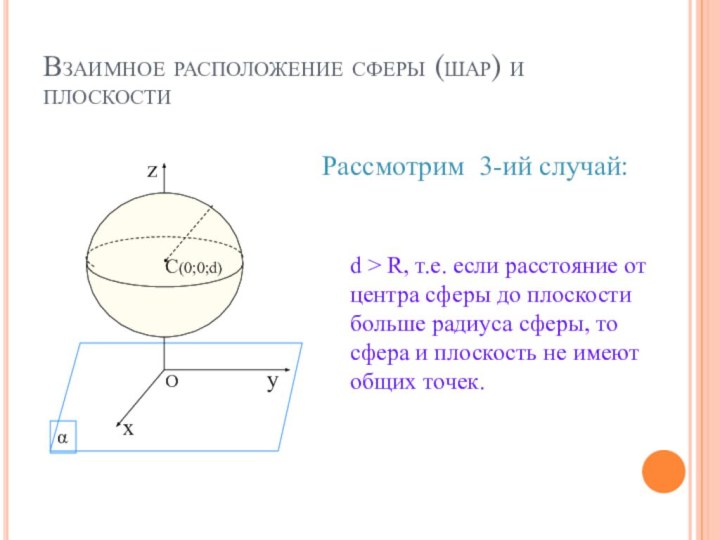
Возможны 3 случая:
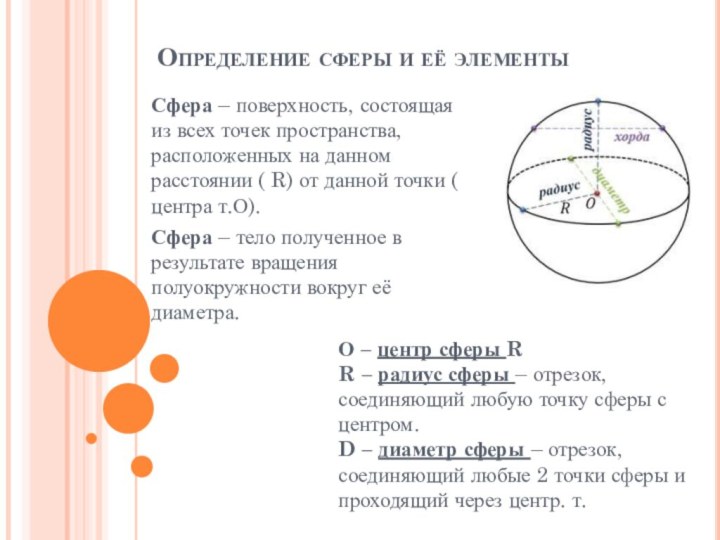
Определение сферы и её элементы
О – центр сферы R
R – радиус сферы – отрезок, соединяющий любую точку сферы с центром.
D – диаметр сферы – отрезок, соединяющий любые 2 точки сферы и проходящий через центр. т.
r
М
r = R2 - d2
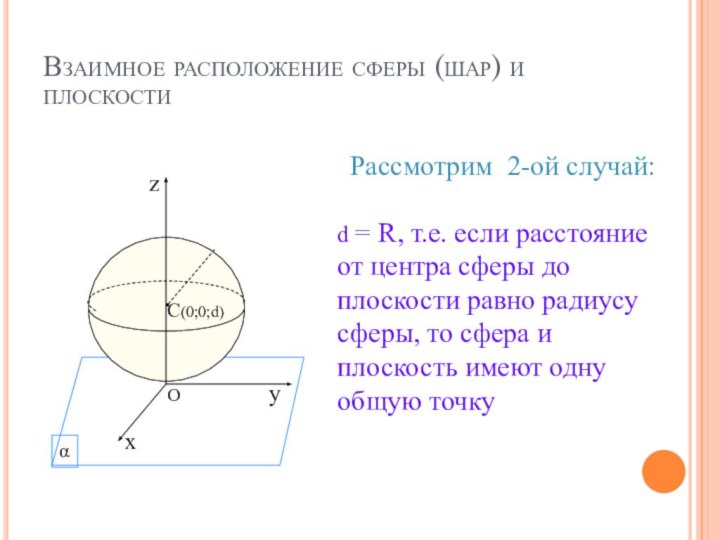
Рассмотрим 1-ый случай:
Напоминание: сечение сферы (шара) плоскостью есть окружность (круг)
Решение:
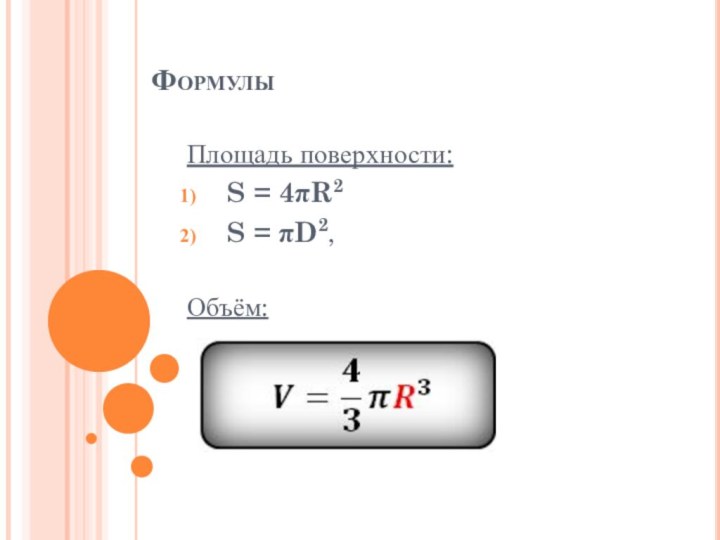
Sсф = 4πR2
Sсф = 4π 62 = 144π см2
Ответ: Sсф = 144π см2