- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Многогранники (9 класс)
Содержание
- 2. Многогранник - это тело, граница которого состоит
- 3. часть пространства, ограниченная совокупностью конечного числа плоских
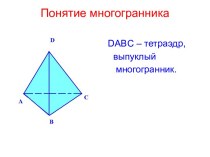
- 4. вершинареброгрань SS,C,A,B – вершиныBC, AB, AS ,SC – ребраASB, SBC, CAB, ASC - грани
- 5. Пространственным аналогом правильного многоугольника на плоскости является многогранник МНОГОУГОЛЬНИКВЕРШИНАСТОРОНАУГОЛМНОГОГРАННИКРЕБРОГРАНЬДВУГРАННЫЙ УГОЛ
- 6. Многогранник называется правильным, если все его грани
- 7. Виды правильных
- 8. История правильных многогранников уходит в глубокую
- 9. Все эти ученые использовали в своих философских
- 10. Тетраэдрсоставлен из четырех равносторонних треугольников. Каждая его
- 11. Гексаэдр (Куб) составлен
- 12. Октаэдр составлен из восьми равносторонних треугольников. Каждая
- 13. Икосаэдрсоставлен из двадцати равносторонних треугольников. Каждая его
- 14. Додекаэдрсоставлен из двенадцати равносторонних пятиугольников. Каждая его
- 15. В каждом правильном многограннике сумма числа граней
- 16. Скачать презентацию
- 17. Похожие презентации
Многогранник - это тело, граница которого состоит из конечного числа плоских многоугольников. Детские кубики, архитектурные сооружения, ювелирные украшения - оглянитесь вокруг, и вы найдете многогранники повсюду.















Слайд 2
Многогранник -
это тело, граница которого состоит
из конечного числа плоских многоугольников.
украшения - оглянитесь вокруг, и вы найдете многогранники повсюду.Слайд 3 часть пространства, ограниченная совокупностью конечного числа плоских многоугольников,
соединенных таким образом, что каждая сторона любого многоугольника является
стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников.МНОГОГРАННИК-
Слайд 5 Пространственным аналогом правильного многоугольника на плоскости является
многогранник
МНОГОУГОЛЬНИК
ВЕРШИНА
СТОРОНА
УГОЛ
МНОГОГРАННИК
РЕБРО
ГРАНЬ
ДВУГРАННЫЙ
УГОЛ
Слайд 6
Многогранник называется правильным,
если все его грани правильные
многоугольники и, кроме того, в каждой вершине сходится одинаковое
число рёбер. Существует 5 видов правильных многогранников.
Слайд 7
Виды правильных многогранников.
ТЕТРАЭДР
ГЕКСАЭДР
ОКТАЭДР
ИКОСАЭДР
ДОДЕКАЭДР
«тетра»
- 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«дедека» -
12«эдра» - грань
Слайд 8
История правильных многогранников
уходит в глубокую древность.
Древние греки
полагали, что материя состоит из 4-х стихий, которым соответствуют
правильные тела:Вода – икосаэдр
Огонь – тетраэдр
Воздух – октаэдр
Земля – куб
Мироздание – додекаэдр
(«пятая сущность»)
Слайд 9
Все эти ученые использовали в своих философских теориях
правильные многогранники.
Платон
Евклид Архимед Кеплер
Слайд 10
Тетраэдр
составлен из четырех равносторонних треугольников.
Каждая его вершина
является вершиной трех треугольников.
Тетраэдр имеет
4 грани,
4
вершины,6 ребер.
Слайд 11
Гексаэдр (Куб)
составлен из шести
квадратов.
Каждая его вершина является вершиной трех квадратов.
Таким
образом, куб имеет6 граней,
8 вершин,
12 ребер
Слайд 12
Октаэдр
составлен из восьми равносторонних треугольников.
Каждая его
вершина является вершиной четырех треугольников.
Октаэдр имеет
8 граней,
6 вершин, 12 ребер.
Слайд 13
Икосаэдр
составлен из двадцати равносторонних треугольников.
Каждая его вершина
является вершиной пяти треугольников.
Икосаэдр имеет
20 граней,
12 вершин, 30 ребер
Слайд 14
Додекаэдр
составлен из двенадцати равносторонних пятиугольников.
Каждая его вершина
является вершиной трех пятиугольников.
Додекаэдр имеет
12 граней,
20
вершин,30 ребер.
Слайд 15 В каждом правильном многограннике сумма числа граней и
вершин равна числу рёбер, увеличенному на 2.
Г+В=Р+2