Презентация на тему по геометрии на тему Параллельность прямой и плоскости (10 класс)

c
Две прямые в пространстве
называются параллельными
если они лежат

в одной плоскости
и не пересекаются

данной прямой, проходит прямая,
параллельная данной, и притом только

одна!

Дано:
α – прямая;
М є α

Доказать:
Ч/з точку М проходит
единственная
прямая b, b α

М
проходит единственная плоскость
2) По опред. прямая b,

проходящая ч/з точку М,
параллельная а, должна лежать в одной
плоскости с точкой М и прямой а.

3) Из планиметрии: ч/з точку М в
плоскости β проходит единственная
прямая, параллельная а.

4) Вывод: b – единственная прямая,
проходящая ч/з точку М, параллельно а!

b∩λ в точке N
Лемма:
Если одна из двух параллельных прямых

пересекает данную плоскость, то и другая
прямая пересекает эту плоскость

N

в какой то плоскости β.
2) Т.к. α∩λ в

точке M, то плоскости λ и β имеют общую точку М, значит по А3 они пересекаются по какой то прямой с.

λ

α

b

М

с

N

β

прямая с пересекает одну из параллельных прямых α, то

она пересекает и вторую прямую b в некоторой точке N.
4) Т.к. прямая с лежит и в λ, то точка N є λ, значит N – общая точка прямой b и плоскости λ.

λ

α

b

М

с

N

β

то они параллельны.
с
b
α
β
Дано:
с // α, с // b.
Доказать:

α // b.

К

в одной плоскости.

1) Пусть точка Кєb, тогда ч/з т.К и прямую α проходит пл. β.
Предположим, что b пересекает β в точке К, тогда по лемме (т.к. с // b) и прямая с будет пересекать β.
Но по условию с // α, и тогда по лемме прямая α пересекает β, что невозможно, т. к. αєβ.
4) Значит наше предположение, что b пересекает β неверно. Значит bєβ.
II. Докажем, что прямые α и b не пересекаются

в пространстве
Прямая АВ
лежит
в плоскости β
Прямая α
и

плоскость ɣ
имеют только
одну общую
точку

λ

Прямая α
и
плоскость
не имеют ни
одной общей
точки

b

точек!

λ
b
b // λ

плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то

она параллельна данной плоскости.

β

b

а

Дано:
а // b, аєβ, bєβ
Доказать:
а // β

а пересекает β.

2) Т.к. а // b по условию, тогда по лемме и b пересекает β.
Противоречие с условием: b лежит в β.
4) Вывод: наше предположение что а // β неверно, значит а // β.

Доказательство

а//α, аєβ, β∩α по прям.

b Доказать: b//а

Утверждение

10

а

β

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

плоскости, то другая прямая либо также параллельна данной плоскости,

либо лежит в этой плоскости

а

а

b

b

β

β

Дано:
а//b и а//β,
тогда либо 1) b//β; 2) bєβ

Утверждение

20

= 7 см;
Аєβ; ВВ1 //

СС1
Найти: СС1

Решение

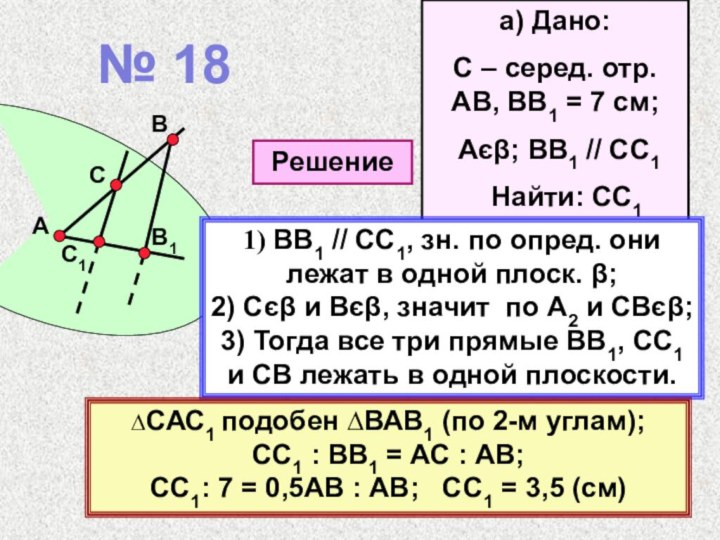
1) ВВ1 // СС1, зн. по опред. они лежат в одной плоск. β; 2) Cєβ и Bєβ, значит по А2 и СВєβ; 3) Тогда все три прямые ВВ1, СС1 и СВ лежать в одной плоскости.

А

С

С1

В

В1

∆САС1 подобен ∆ВАВ1 (по 2-м углам); СС1 : ВВ1 = АС : АВ; СС1: 7 = 0,5АВ : АВ; СС1 = 3,5 (см)

№ 18

АС:СВ=3:2,

ВВ1 = 20 см

Решение

1) ВВ1 // СС1, зн. по опред. они лежат в одной плоск. β; Cєβ и Bєβ, значит по А2 и СВєβ, тогда все три прямые ВВ1, СС1 и СВ лежать в одной плоскости.

А

С

С1

В

В1

2) ∆САС1 подобен ∆ВАВ1 (по 2-м углам); СС1 : ВВ1 = АС : АВ; СС1: 20 = 3 : (3+2); СС1 = 20·3:5 = 12 (см)

Найти: СС1

ɣ

№ 18

Аєα, Вєα, Сєα, М-середина АС, N-середина СВ

Доказать: MN//α

Доказательство

1) Проведём отр. АВ;

2) По А2: АВ є α;

3) MN – средняя лин. ∆АВС;

4) MN // АВ, и по Т-5: MN//α.

№ 22

М

АВСD- прямоуг.

М є пл.АВСD Доказать: СD//пл.АМВ

А

В

М

С

D

Доказательство

1) АВ // СD (по условию);

2) АВ є пл. АВМ;

3) По Т-5: CD // пл.АВМ

№ 23

М є пл.АВСD; АВСD - трапец. АD

– основан. Доказать: АD//пл.ВСМ

1) АD//ВС, т.к. АВСD – трапец.

№ 24

Доказательство

2) ВС є пл.ВМС,

3) По Т-5: АD // пл.ВСМ

= MN; L // MN;

Lєα, Lєβ;

L //α и L // β

L

β

α

М

N

1) L //MN, MNєα, зн. по Т-5 L // α;

Доказать:

№ 25

Доказательство

2) L // MN, MNєβ, зн. по Т-5 L // β

АВ – отрезок, СєАВ, АВ:ВС = 4:3, Вєα, СD//α, СD=12cм
Доказать, что прям. АD∩α в т.Е, ВЕ-?

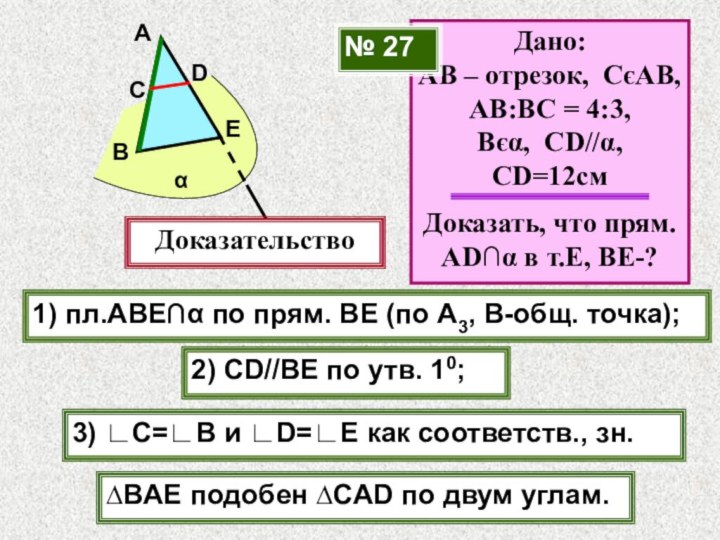
1) пл.АВЕ∩α по прям. ВЕ (по А3, В-общ. точка);

№ 27

Доказательство

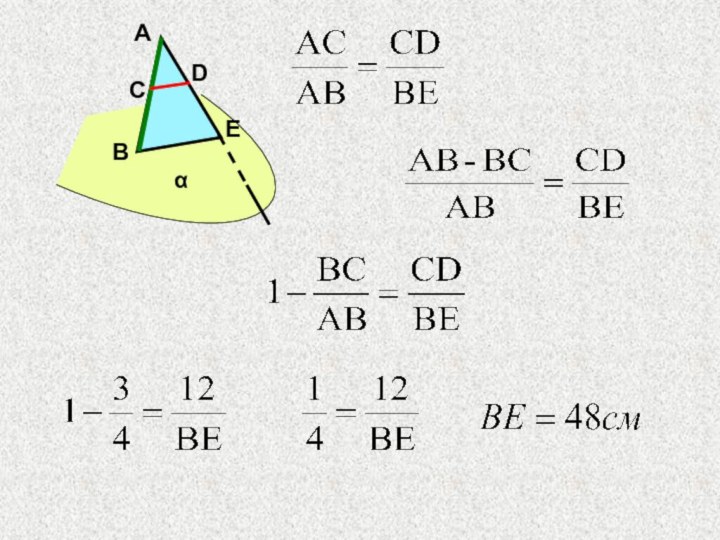
2) СD//ВЕ по утв. 10;

3) ∟C=∟B и ∟D=∟E как соответств., зн.

∆BАE подобен ∆CAD по двум углам.

ВD:DА=2:3; Вєα; Cєα; α//DE

Найти: ВС

α

Решение

1) DЕ // α; DE є пл.АВС, зн. DЕ // ВС; 2) ∆BAC подобен ∆DAE; АВ=2ч+3ч=5ч 3) ВС:DЕ=АВ:АD; ВС:5=5:3; ВС=25/3

?