Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Положение плоскости относительно плоскостей проекций

Содержание

Плоскости частного положения
Положение плоскости относительно плоскостей проекций Плоскости частного положения Плоскость, перпендикулярная к плоскости проекций, называется проецирующейОсобенности проецирующих плоскостей:– одна проекция любого хА2В2С2С1А1В1α( АВС)⊥П1Горизонтально – проецирующая плоскостьxαП1αxУгол наклона к П2 xA2B2A0BC βП2βП1С2П2П1β⊥П2δδ( АВС)∈β; β⊥П2; xA0BC γП2γП1П2П1A3С1B1П3αхА3В3С3С1А1В1В2А2С2γ( АВС)⊥П3Профильно – Плоскость, параллельная к плоскости проекций, называется плоскостью уровняОсобенностиплоскостей уровня:Плоскости уровня– любая плоская АВС||П1⇒ А1В1С1=| АВС|A1B1AA2Ax0BB2αllП1С1С2αГоризонтальная плоскостьП2П1АВС∈α; АВС Плоскости уровняхА2В2С2С1А1В1хА2В2С2С1А1В1хА3В3С3С1А1В1////α( АВС) ll П1Натуральная величина////нвβ( АВС) ll П2В2А2С2////////γ( АВС) ll П3нвгоризонтальнаяфронтальнаяпрофильнаяzy
Слайды презентации

Слайд 2 Плоскости частного положения

Плоскости частного положения

Слайд 3 Плоскость, перпендикулярная к плоскости проекций, называется проецирующей
Особенности
проецирующих

Плоскость, перпендикулярная к плоскости проекций, называется проецирующейОсобенности проецирующих плоскостей:– одна проекция

плоскостей:
– одна проекция любого элемента, расположенного
– в проецирующей плоскости,

совпадает
с соответствующим следом этой плоскости

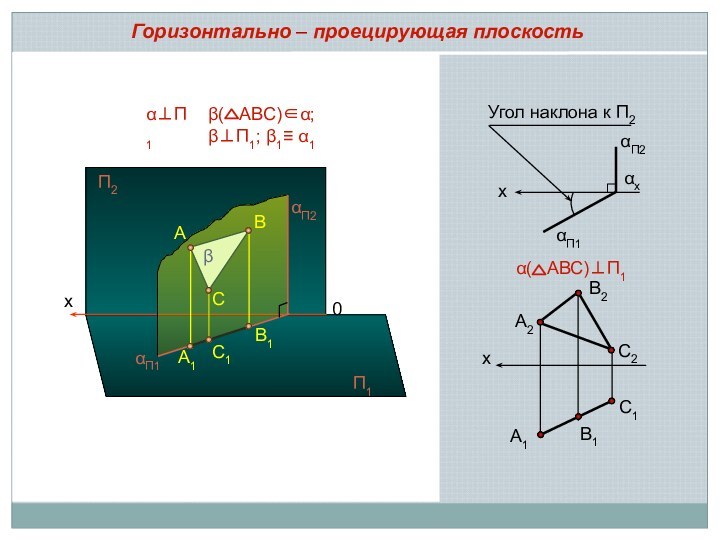
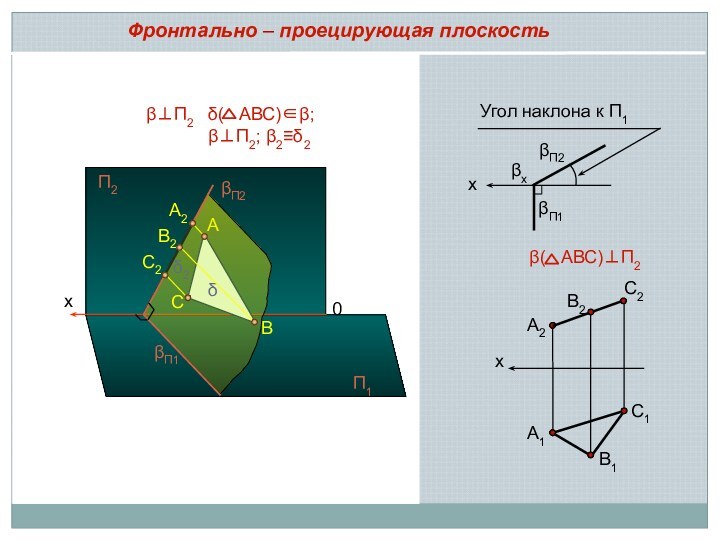
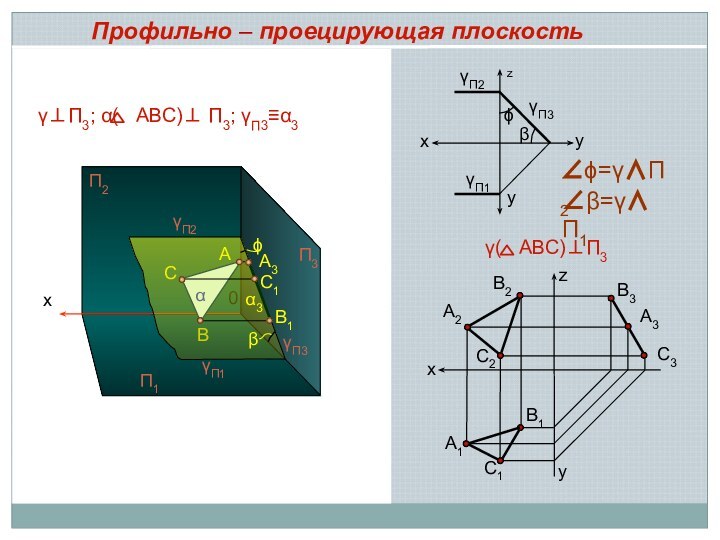
– угол наклона заданной плоскости к плоскости проекций на эпюре проецируется в натуральную величину

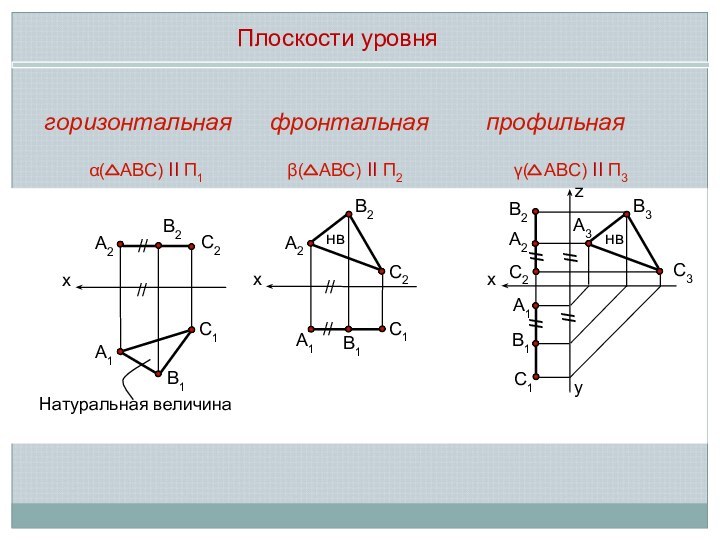
Проецирующие плоскости

Слайд 4
х



А2
В2
С2
С1
А1
В1










α( АВС)⊥П1
Горизонтально – проецирующая плоскость


x
αП1
αx

Угол наклона к

хА2В2С2С1А1В1α( АВС)⊥П1Горизонтально – проецирующая плоскостьxαП1αxУгол наклона к П2 xA1B1A0BC αП2С1П2П1α⊥П1ββ( АВС)∈α; β⊥П1; β1≡ α1αП1αП2

П2





x

A1
B1
A
0

B
C
αП2









С1
П2
П1
α⊥П1
β
β(

АВС)∈α; β⊥П1; β1≡ α1




αП1

αП2

Слайд 5




x

A2
B2
A
0

B
C

xA2B2A0BC βП2βП1С2П2П1β⊥П2δδ( АВС)∈β; β⊥П2; β2≡δ2хА2В2С2С1А1В1β( АВС)⊥П2xβП1βП2βxУгол наклона к П1Фронтально – проецирующая плоскостьδ2


βП2
βП1




С2
П2
П1
β⊥П2
δ
δ( АВС)∈β; β⊥П2; β2≡δ2












х



А2
В2
С2
С1
А1
В1










β( АВС)⊥П2


x
βП1
βП2
βx

Угол наклона к

П1


Фронтально – проецирующая плоскость

δ2



Слайд 6




x

A
0
B
C

xA0BC γП2γП1П2П1A3С1B1П3αхА3В3С3С1А1В1В2А2С2γ( АВС)⊥П3Профильно – проецирующая плоскостьzyxγП1γП2γП3zууϕβ∠ϕ=γ∧П2∠β=γ∧П1γП3α3γ⊥П3; α( АВС)⊥ П3; γП3≡α3ϕβ


γП2
γП1
П2
П1













A3
С1
B1
П3
α

х



А3
В3
С3
С1
А1
В1






















В2
А2
С2
γ( АВС)⊥П3
Профильно – проецирующая плоскость
z
y








x
γП1
γП2
γП3

z
у
у

ϕ
β
∠ϕ=γ∧П2
∠β=γ∧П1
γП3
α3
γ⊥П3; α( АВС)⊥

П3; γП3≡α3


ϕ


β





Слайд 7 Плоскость,
параллельная к плоскости проекций, называется плоскостью уровня
Особенности
плоскостей

Плоскость, параллельная к плоскости проекций, называется плоскостью уровняОсобенностиплоскостей уровня:Плоскости уровня– любая

уровня:
Плоскости уровня
– любая плоская фигура,
расположенная в плоскости уровня,


проецируется на параллельную ей плоскость проекций без искажения, – т.е. в натуральную величину

Слайд 8

















АВС||П1⇒ А1В1С1=|

АВС||П1⇒ А1В1С1=| АВС|A1B1AA2Ax0BB2αllП1С1С2αГоризонтальная плоскостьП2П1АВС∈α; АВС ll П1АВС ll

АВС|
A1
B1
A
A2
Ax
0

B
B2
αllП1



С1


С2



α
Горизонтальная плоскость









П2
П1




АВС∈α;
АВС ll П1

АВС ll А1В1С1



С

  • Имя файла: polozhenie-ploskosti-otnositelno-ploskostey-proektsiy.pptx
  • Количество просмотров: 144
  • Количество скачиваний: 0
- Предыдущая Кормушка
Следующая - Интерьер жилого помещения

Похожие презентации

Презентация по геометрии на тему Метод следов Презентация по геометрии на тему Метод следов 183
Презнтация к уроку геометрии в 7 классе Равнобедренный треугольник и его свойства. Презнтация к уроку геометрии в 7 классе Равнобедренный треугольник и его свойства. 165
Взаимное расположение прямой и окружности Взаимное расположение прямой и окружности 161
Геометрия ЕГЭ (11 класс ) Геометрия ЕГЭ (11 класс ) 82
Вписанная и описанная окружность 8 класс Вписанная и описанная окружность 8 класс 147
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ 205
Решение задач В4 Решение задач В4 146
Треугольники Треугольники 188
Теорема Пифагора по геометрии Теорема Пифагора по геометрии 184
Египетский треугольник Египетский треугольник 156
Задачи на готовых чертежах Задачи на готовых чертежах 154
Презентация к уроку по геометрии Обобщающий урок по теме Равенство треугольников Презентация к уроку по геометрии Обобщающий урок по теме Равенство треугольников 162
Квадратные корни Квадратные корни 157
Теорема синусов Теорема синусов 157
Презентация по математике на тему Свойства магического квадрата и других фигур Презентация по математике на тему Свойства магического квадрата и других фигур 162
Начальные сведения о геометрии Начальные сведения о геометрии 143
Длина отрезка Длина отрезка 180
Соотношения между сторонами и углами прямоугольного треугольника Соотношения между сторонами и углами прямоугольного треугольника 134
Презентация по геометрии Площадь треугольника (8 класс) Презентация по геометрии Площадь треугольника (8 класс) 160
Теорема Пифагора Теорема Пифагора 157
Тема Существование треугольника, равного данному Тема Существование треугольника, равного данному 168
Параллельные прямые и их признаки Параллельные прямые и их признаки 167
Измерение объема тела Измерение объема тела 173
Правильные и полуправильные многогранники Правильные и полуправильные многогранники 164
Презентация по геометрии на тему Четырехугольники (8 класс) Презентация по геометрии на тему Четырехугольники (8 класс) 151
Понятие многогранника Понятие многогранника 321
Презентация по теме: Цилиндр Презентация по теме: Цилиндр 164
Угол между прямыми Угол между прямыми 170
Измерение расстояний. Масштаб Измерение расстояний. Масштаб 351
Правильные выпуклые многогранники Правильные выпуклые многогранники 142