Успешного усвоения нового материала
Основная мысль урока
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи,
то решайте их. (Д.Пойа)
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




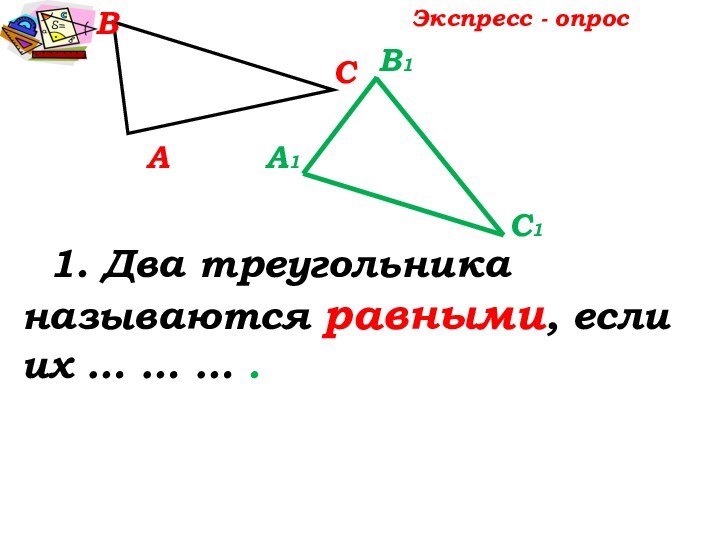
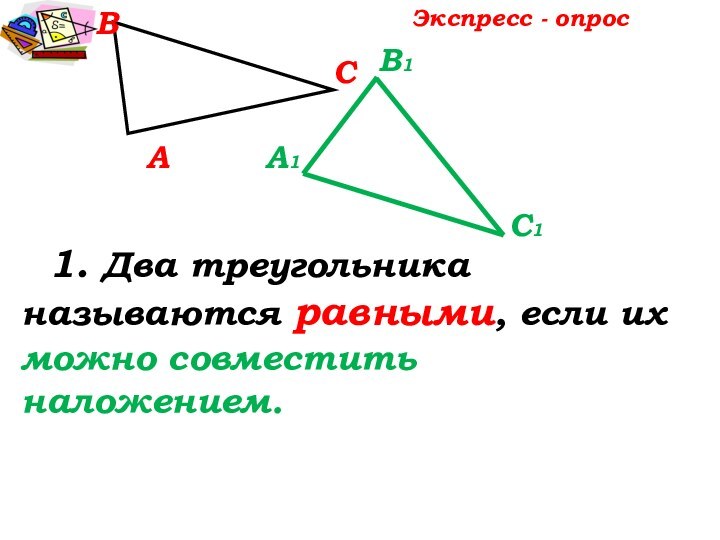


















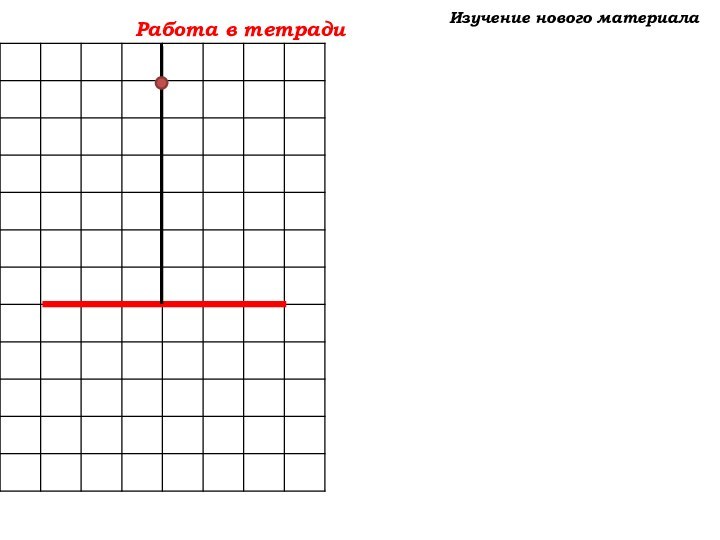
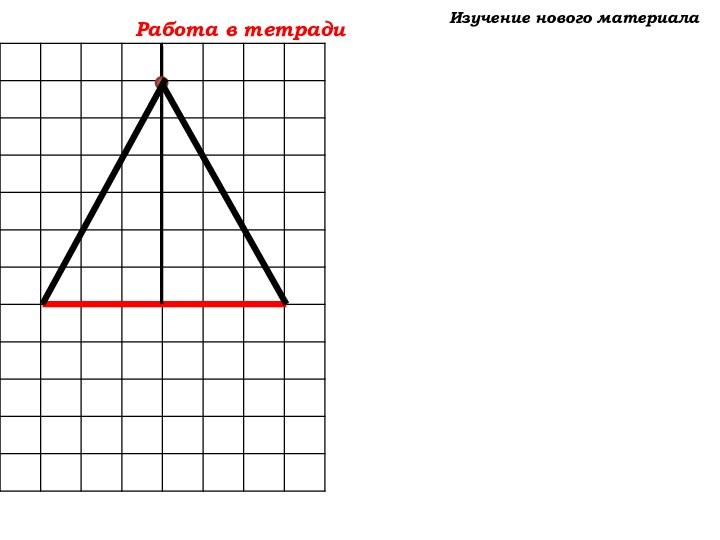

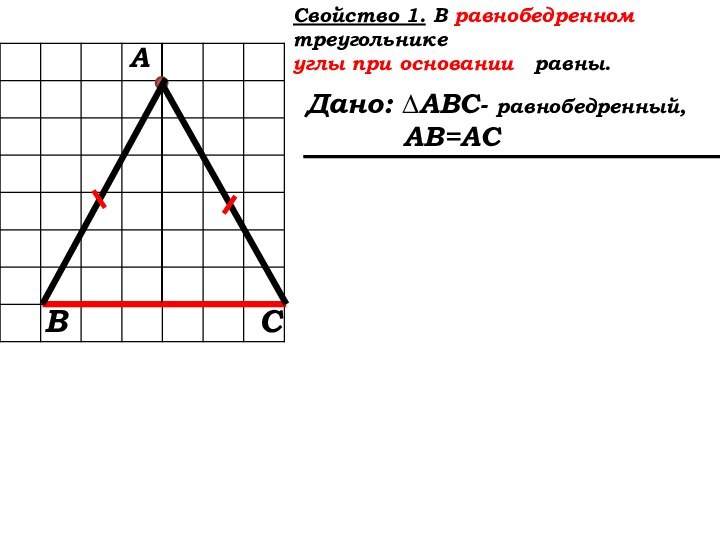
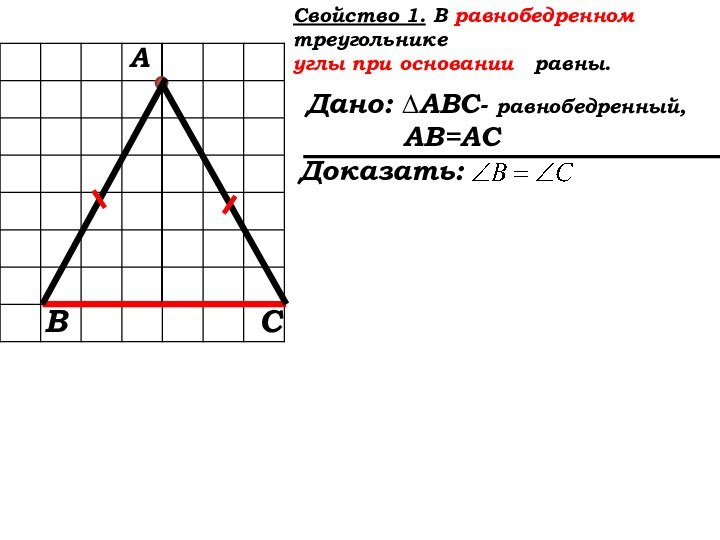



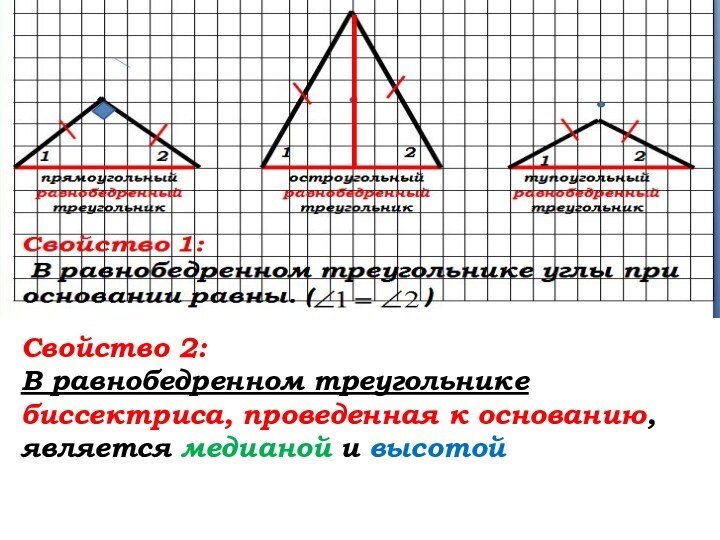



Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи,
то решайте их. (Д.Пойа)
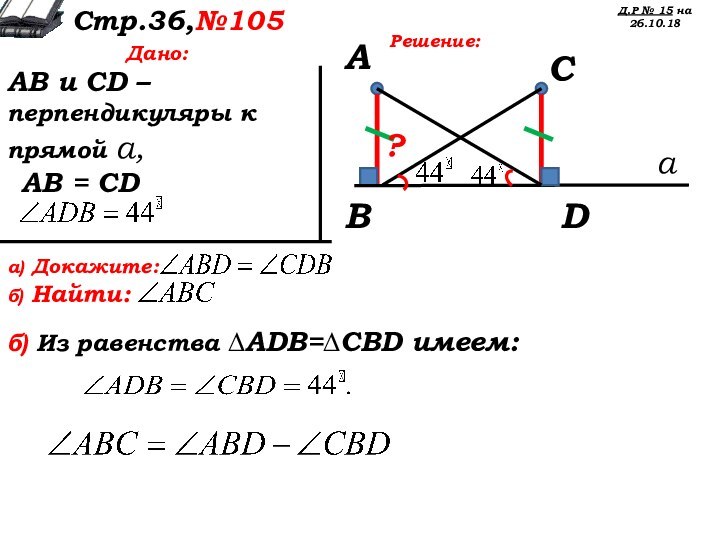
АВ = CD
а) Докажите:
б) Найти:
Решение:
С
D
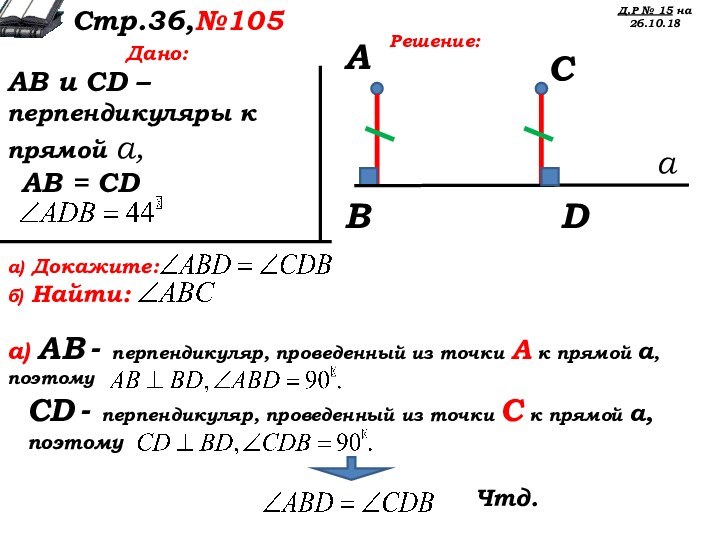
CD - перпендикуляр, проведенный из точки С к прямой а, поэтому
Чтд.
Решение:
С
D
?
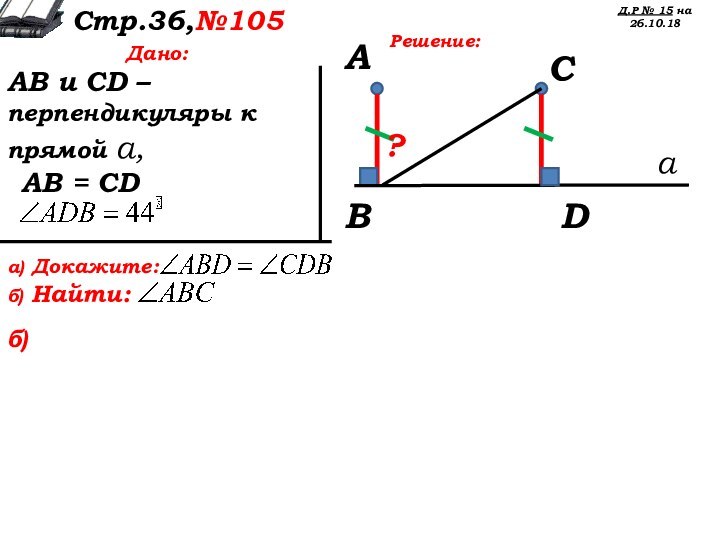
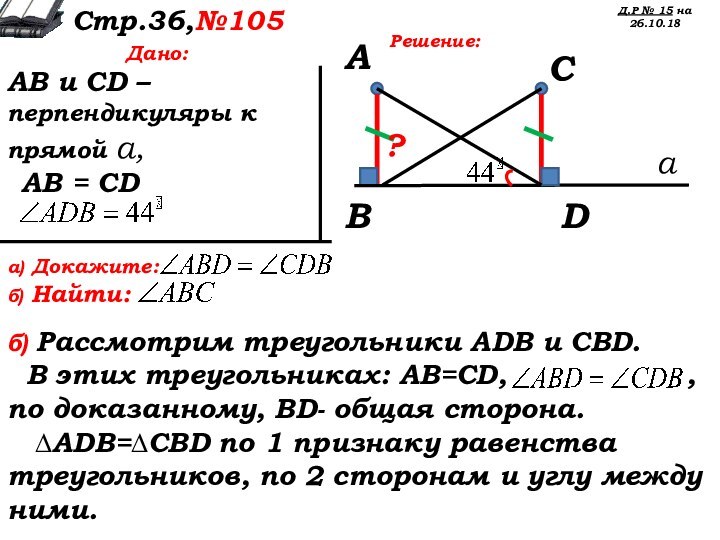
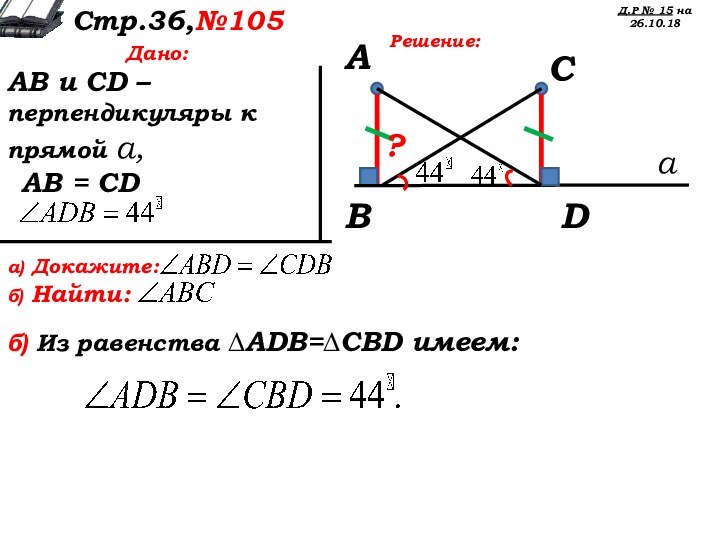
Дано:
АВ и CD – перпендикуляры к прямой а,
АВ = CD
а) Докажите:
б) Найти:
Решение:
С
D
?
АВ = CD
а) Докажите:
б) Найти:
Решение:
С
D
?
АВ = CD
а) Докажите:
б) Найти:
Решение:
С
D
?
АВ = CD
а) Докажите:
б) Найти:
Решение:
С
D
?
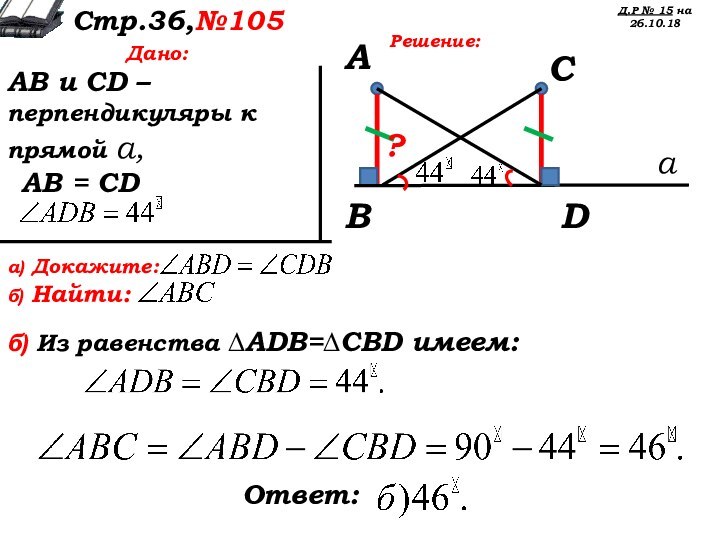
Ответ:
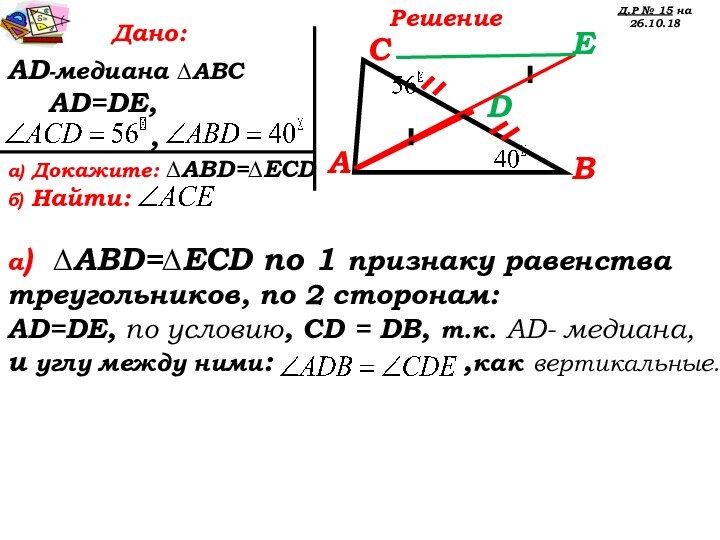
а) Докажите: ∆AВD=∆ЕCD
б) Найти:
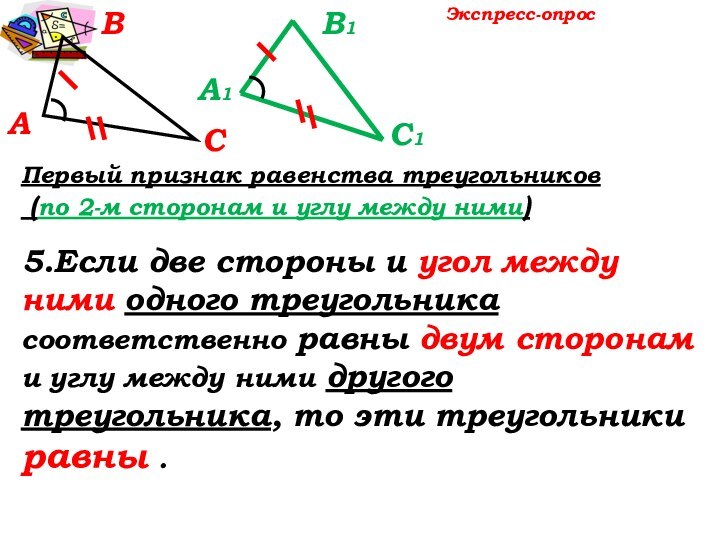
а) ∆AВD=∆ЕCD по 1 признаку равенства
треугольников, по 2 сторонам:
AD=DE, по условию, CD = DB, т.к. AD- медиана,
и углу между ними: ,как вертикальные.
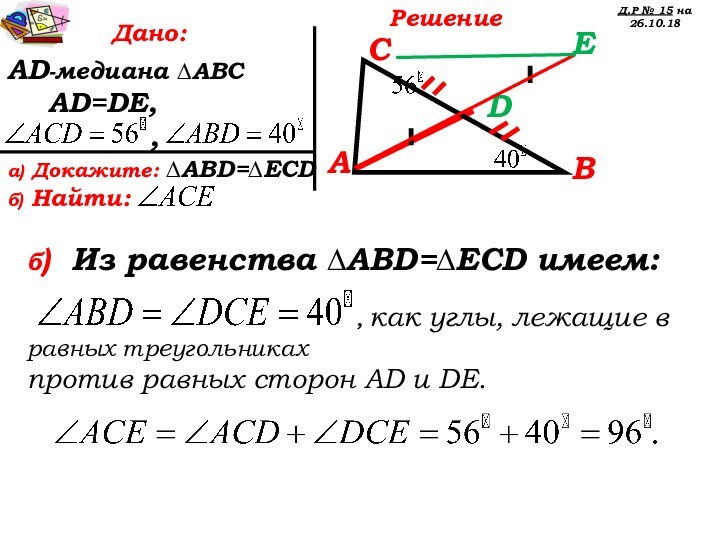
а) Докажите: ∆AВD=∆ЕCD
б) Найти:
б) Из равенства ∆AВD=∆ЕCD имеем:
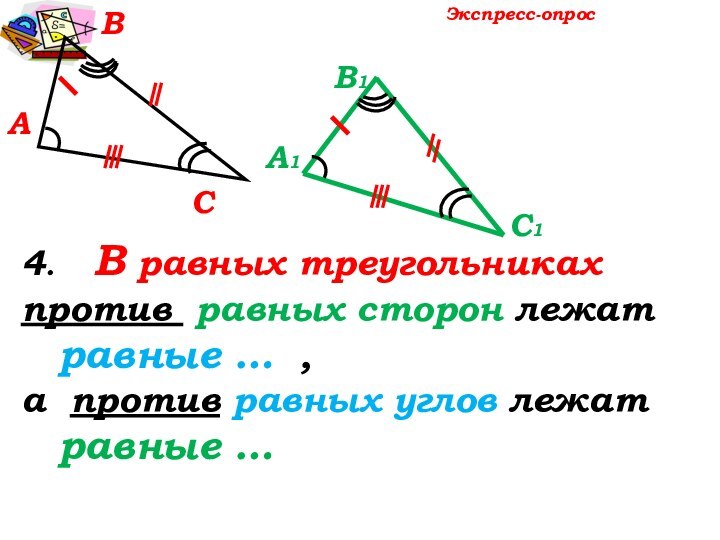
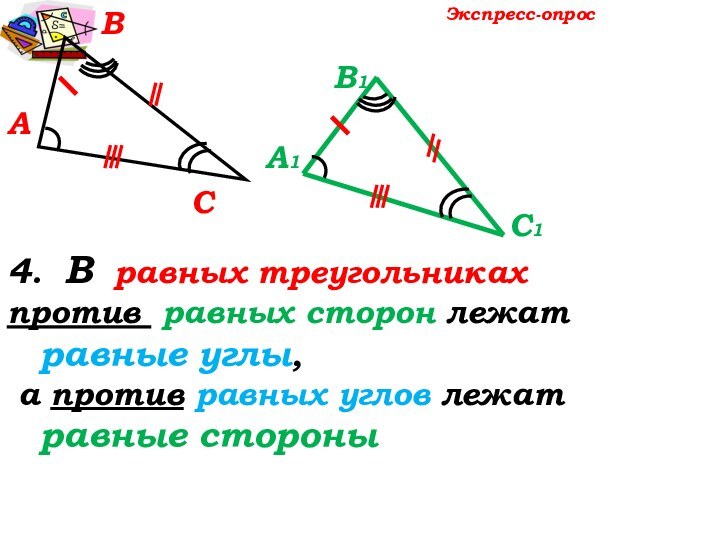
, как углы, лежащие в равных треугольниках
против равных сторон AD и DE.
А1
С1
В1
А1
С1
В1
А1
С1
В1
А1
С1
В1
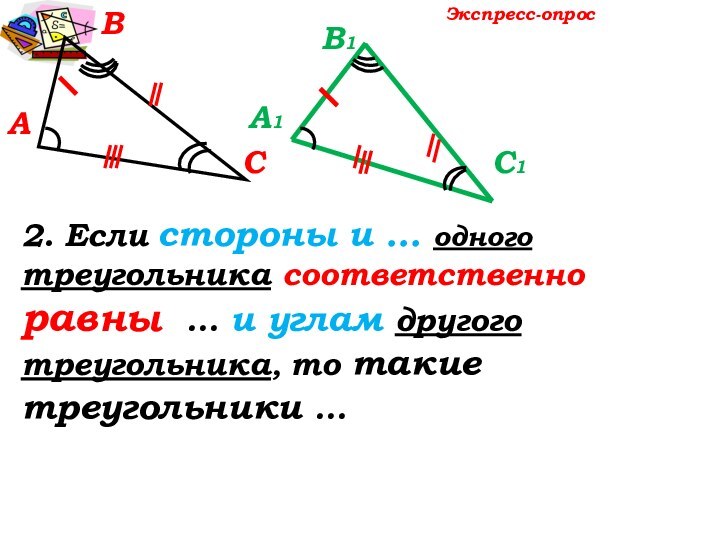
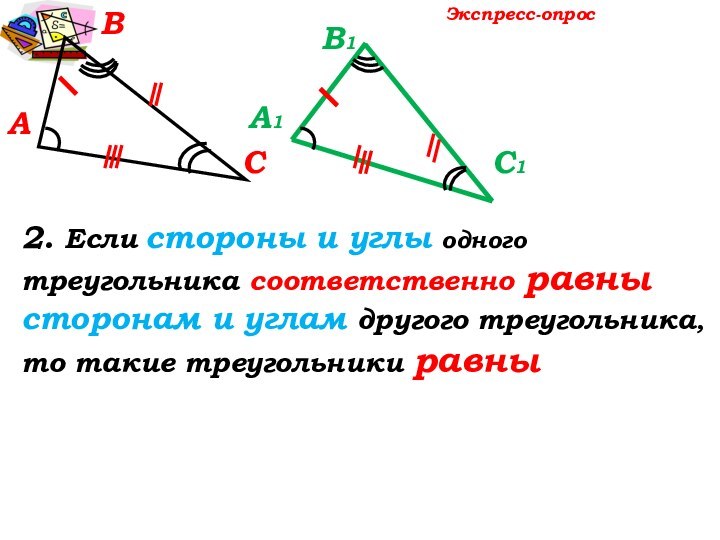
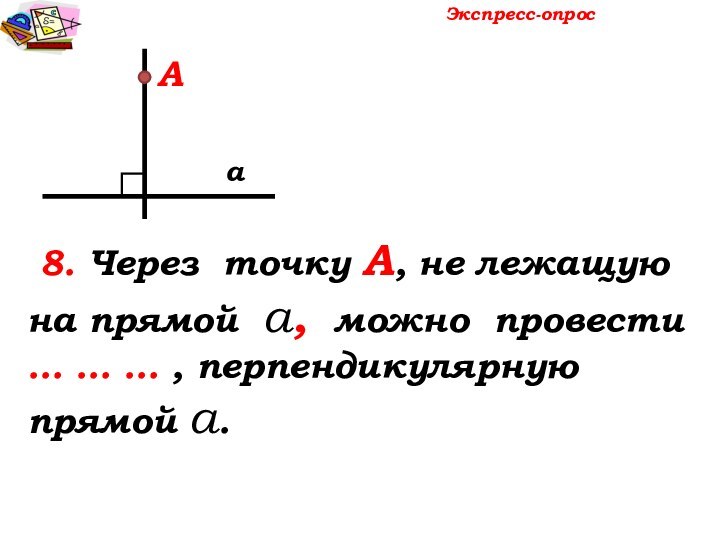
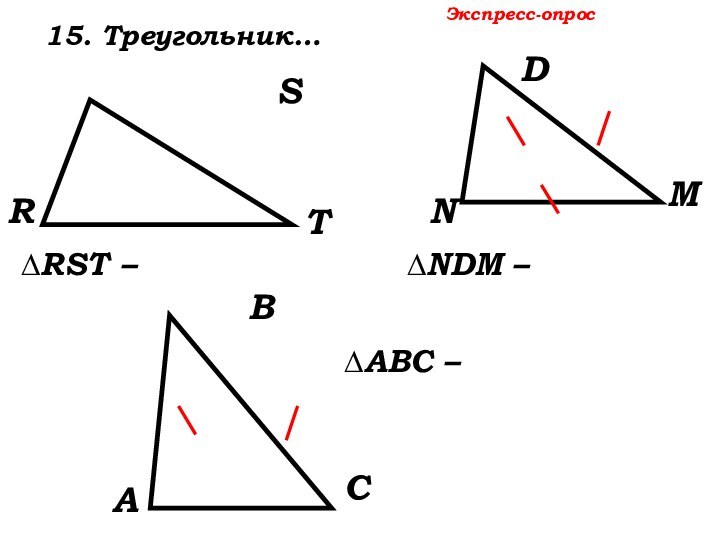
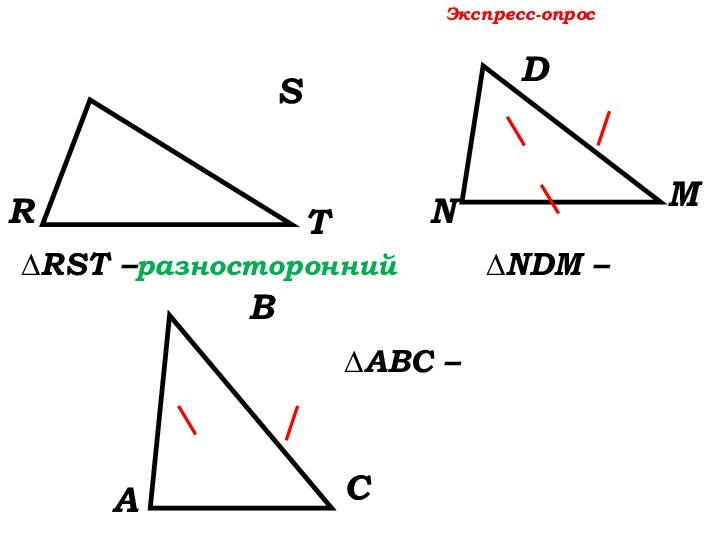
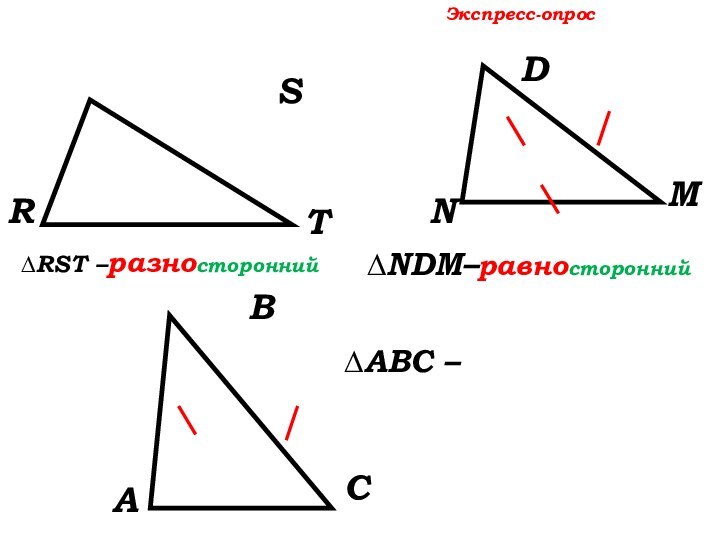
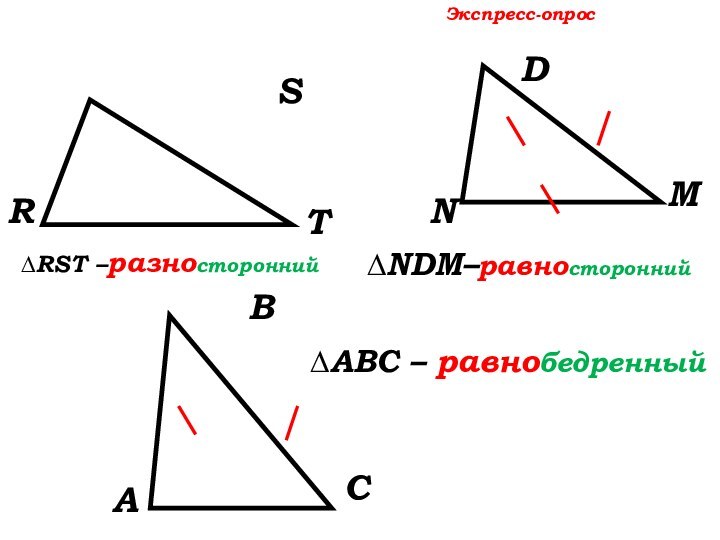
Экспресс-опрос
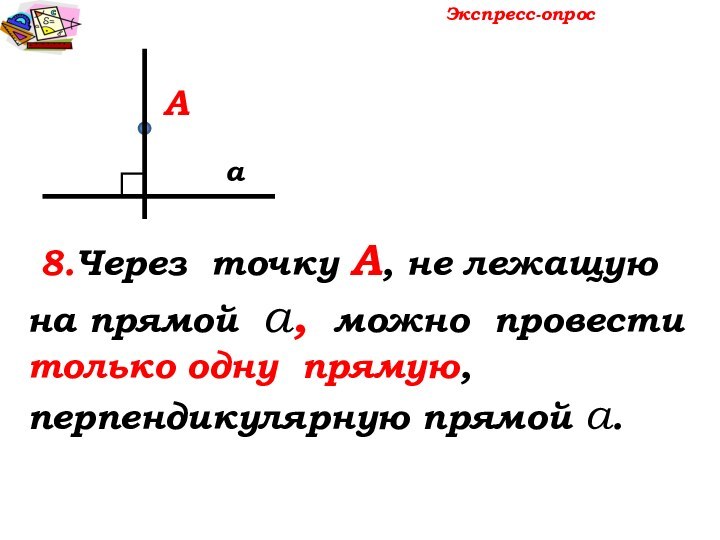
Экспресс-опрос
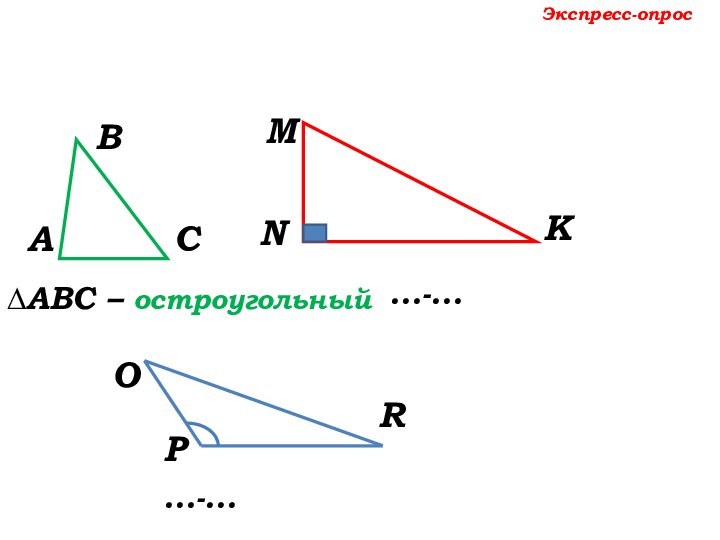
Экспресс-опрос
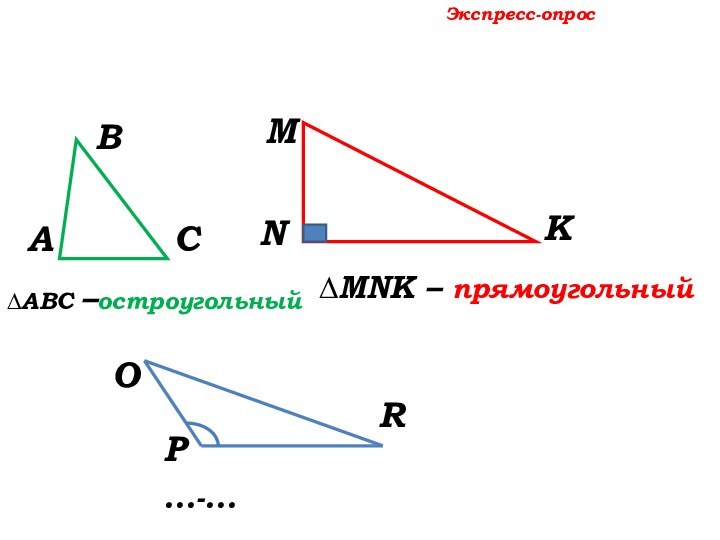
Экспресс-опрос
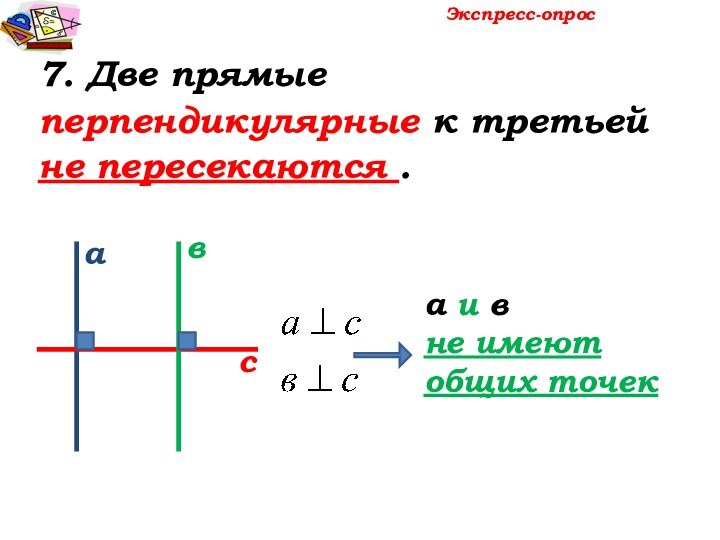
а
в
с
Экспресс-опрос
Экспресс-опрос
Экспресс-опрос
Экспресс-опрос
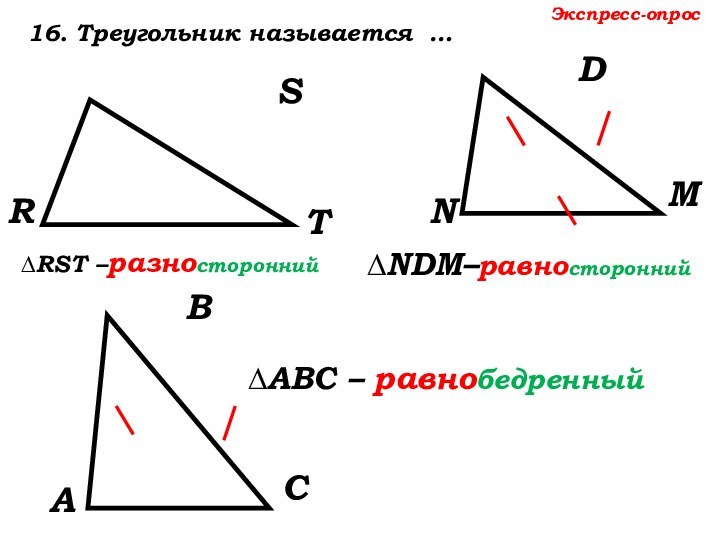
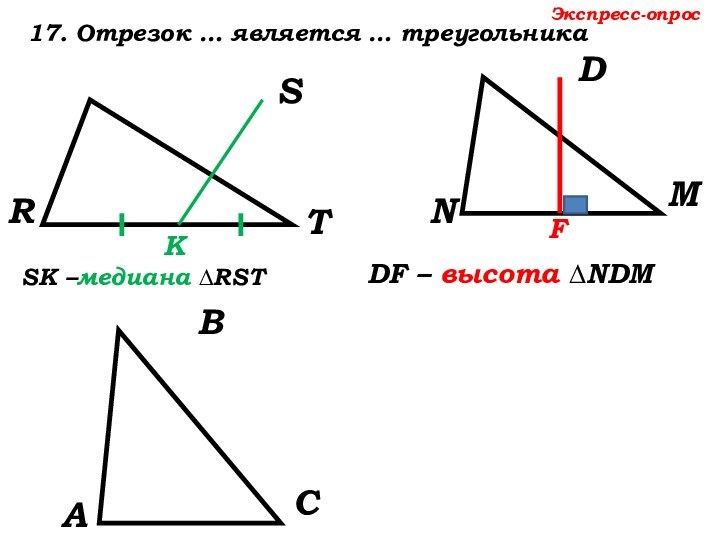
13. Высоты треугольника
или их …
пересекаются в одной точке
Экспресс-опрос
13. Высоты треугольника
или их …
пересекаются в одной точке
Экспресс-опрос
13. Высоты треугольника
или … …
пересекаются в одной точке
Экспресс-опрос
13. Высоты треугольника
или их продолжения
пересекаются в одной точке
Экспресс-опрос
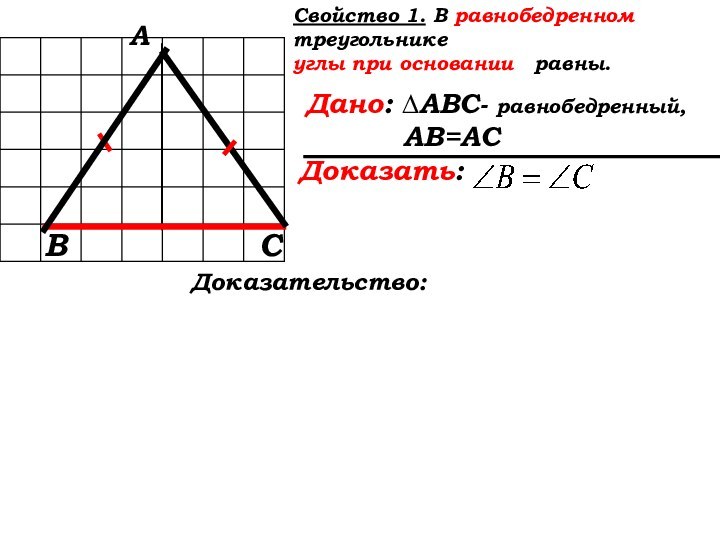
В
А
С
В
А
С
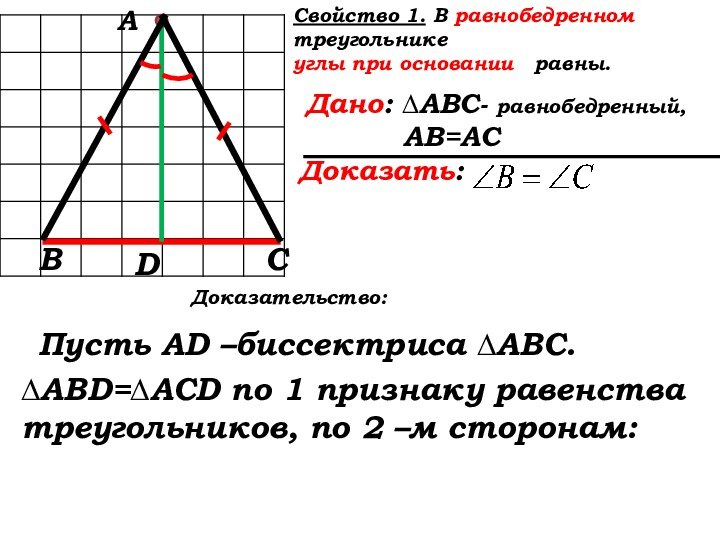
Доказательство:
В
А
С
D
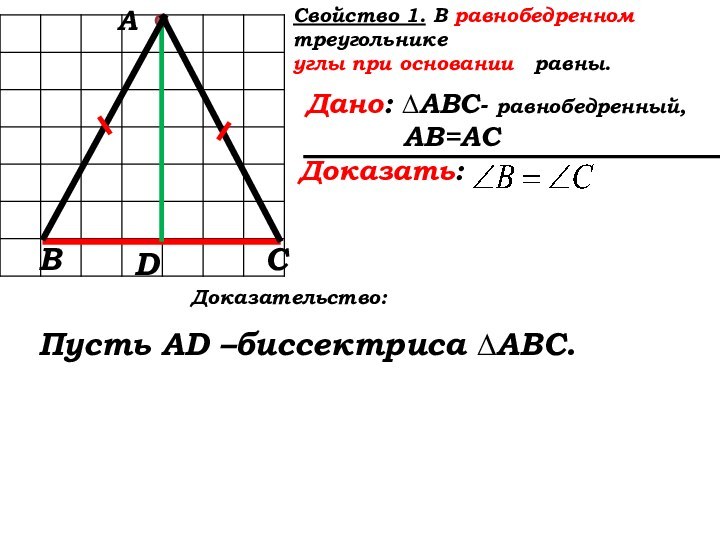
Доказательство:
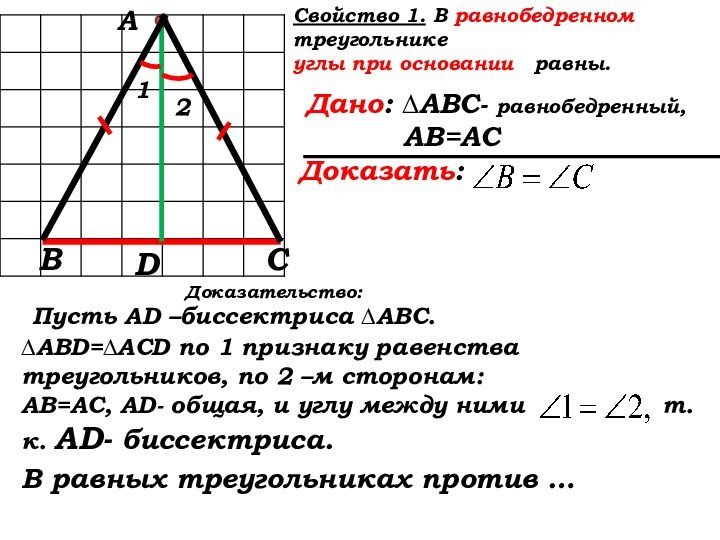
Пусть AD –биссектриса ∆АВС.
В
А
С
D
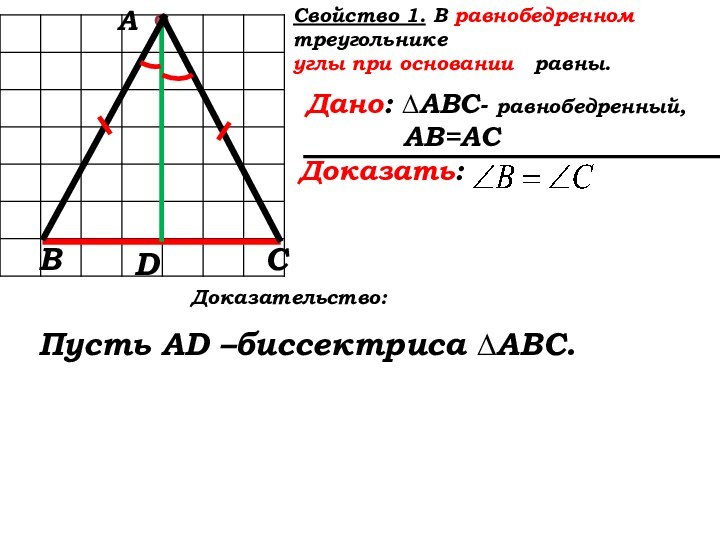
Доказательство:
Пусть AD –биссектриса ∆АВС.
В
А
С
D
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆…
В
А
С
D
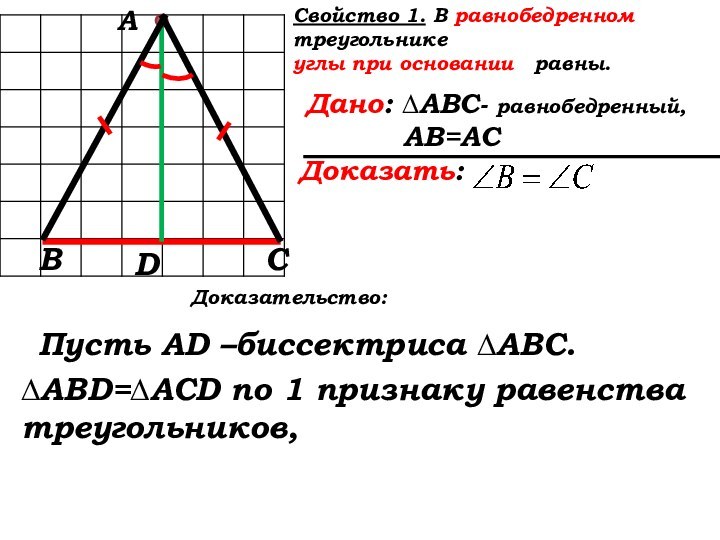
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников,
В
А
С
D
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
В
А
С
D
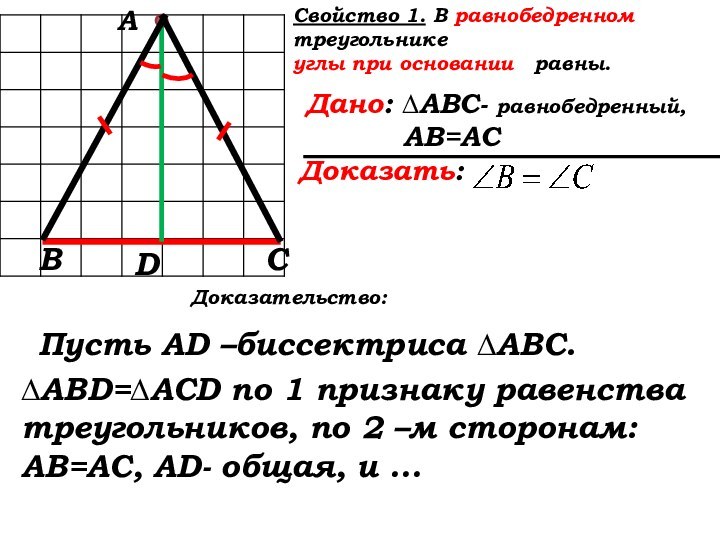
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и …
В
А
С
D
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними
В
А
С
D
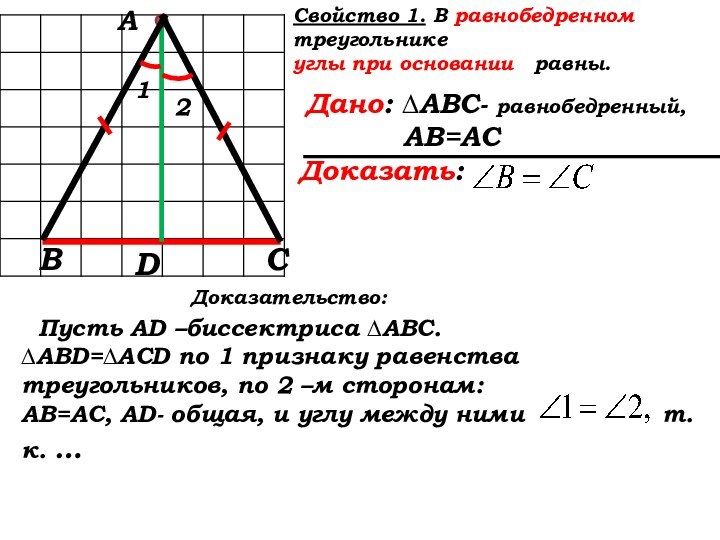
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними т.к. …
1
2
В
А
С
D
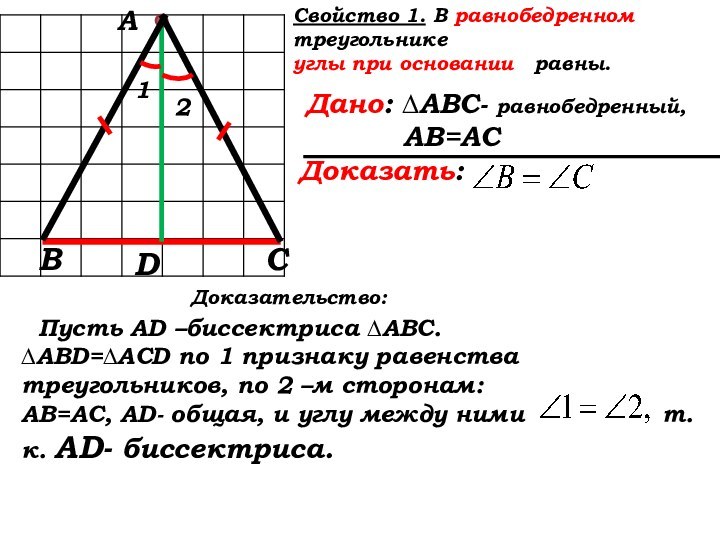
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними т.к. AD- биссектриса.
1
2
В
А
С
D
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними т.к. AD- биссектриса.
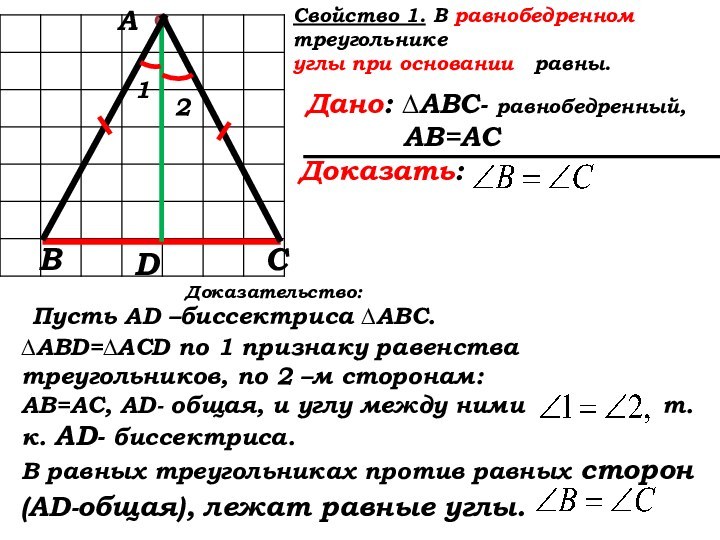
В равных треугольниках против …
1
2
В
А
С
D
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними т.к. AD- биссектриса.
В равных треугольниках против равных сторон (АD-общая), …
1
2
В
А
С
D
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними т.к. AD- биссектриса.
В равных треугольниках против равных сторон (АD-общая), лежат равные углы.
1
2
В
А
С
D
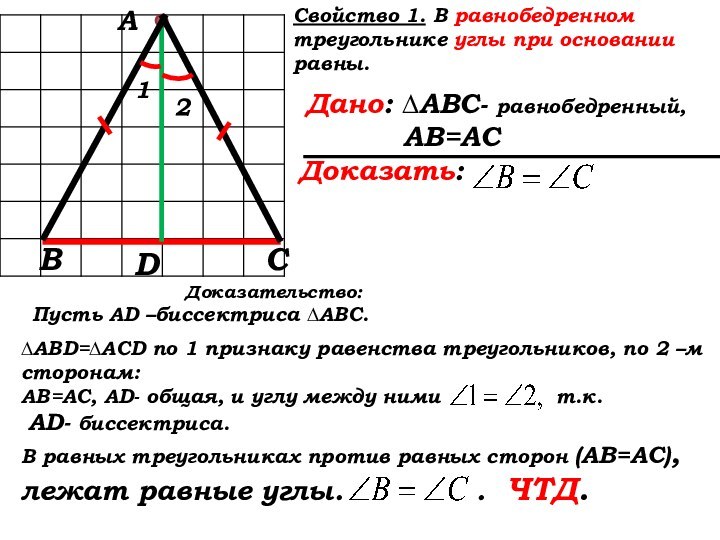
Доказательство:
Пусть AD –биссектриса ∆АВС.
∆ABD=∆ACD по 1 признаку равенства треугольников, по 2 –м сторонам:
АВ=АС, AD- общая, и углу между ними т.к.
AD- биссектриса.
В равных треугольниках против равных сторон (АВ=АС), лежат равные углы. . ЧТД.
1
2
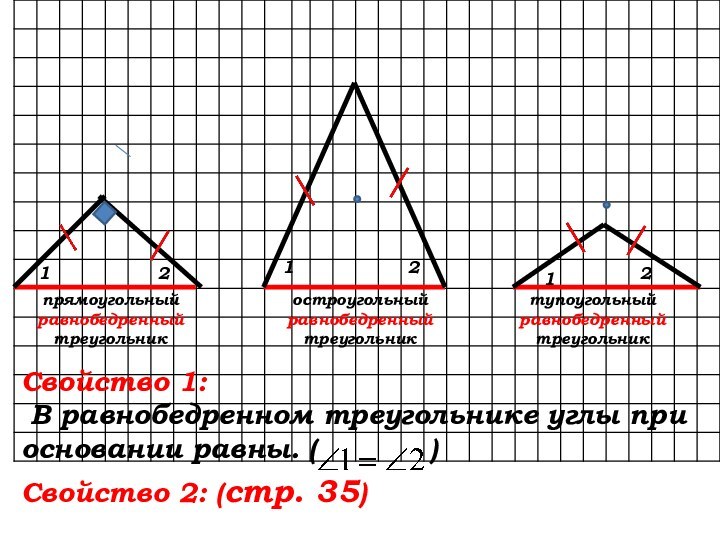
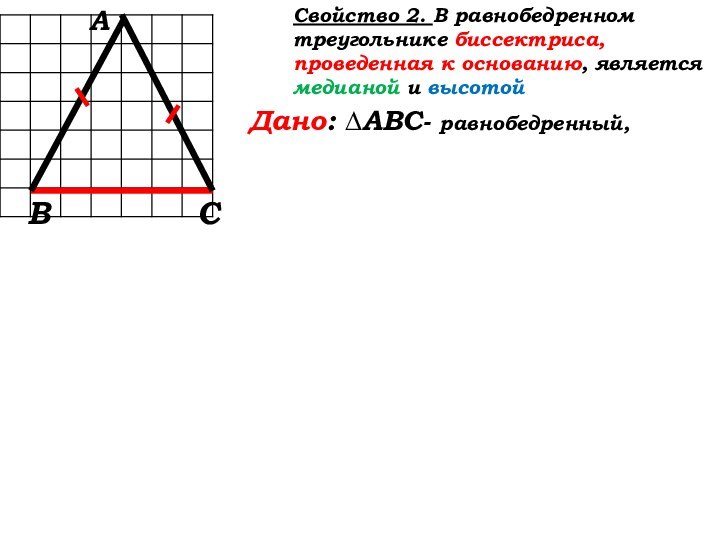
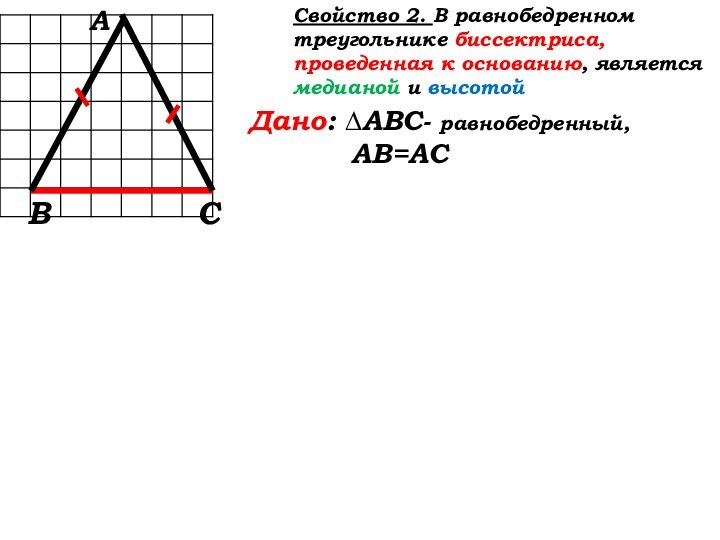
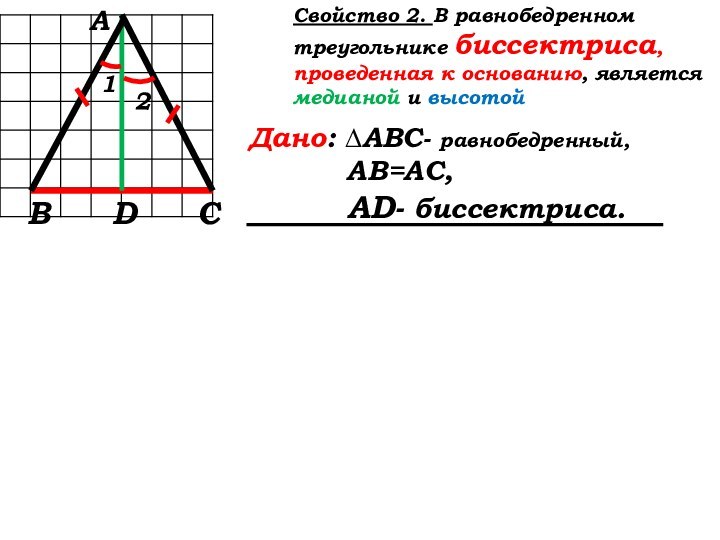
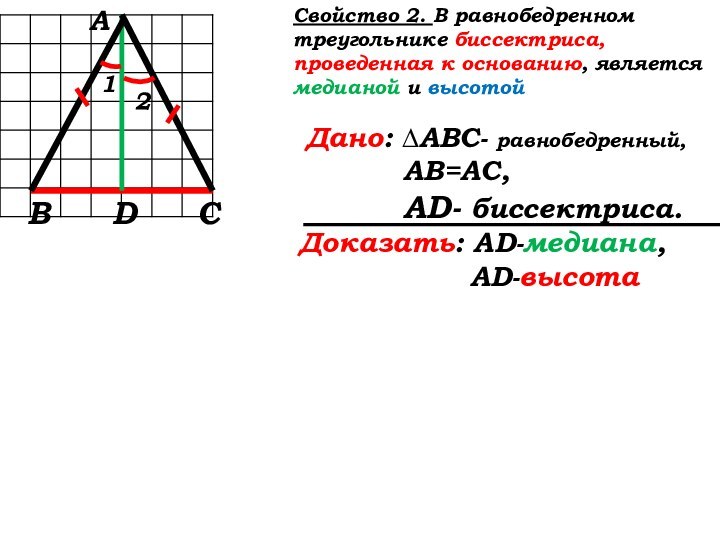
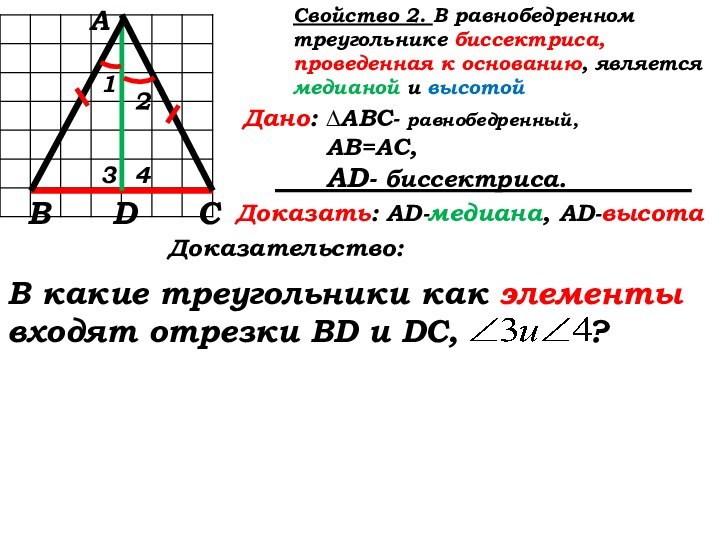
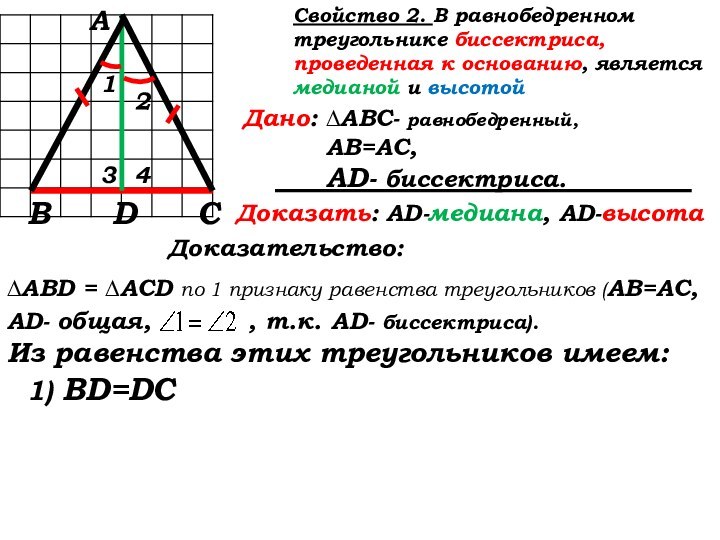
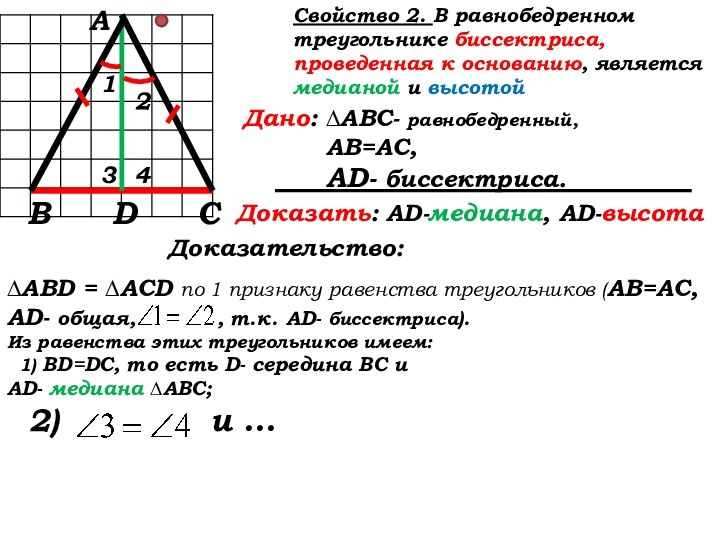
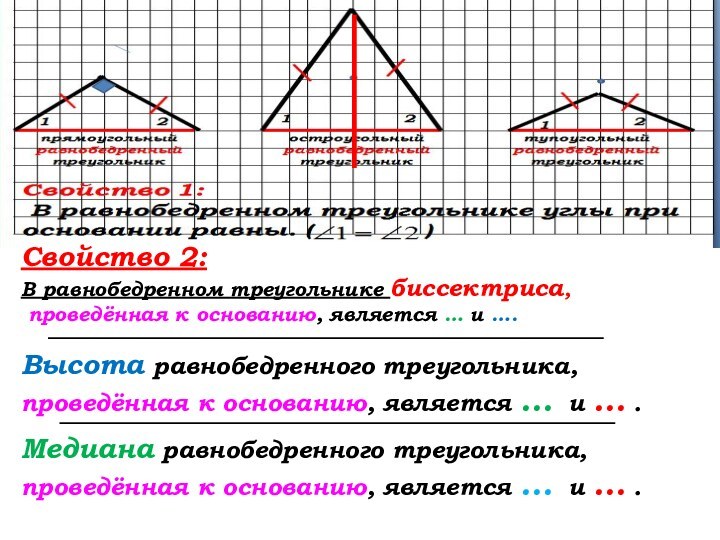
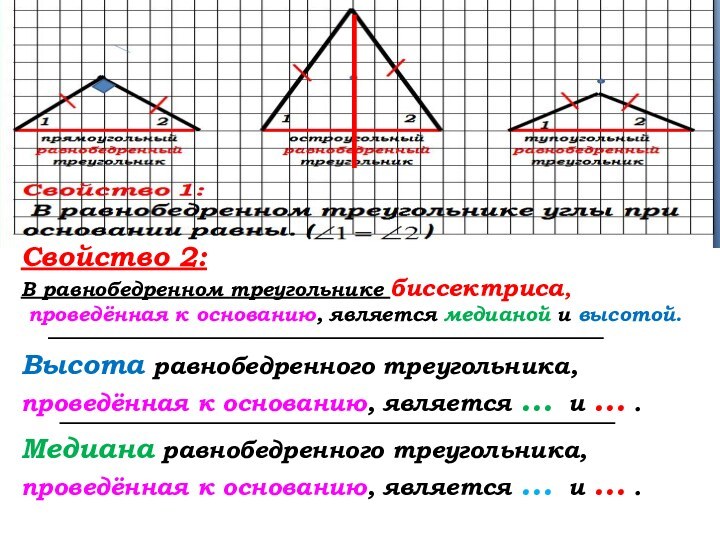
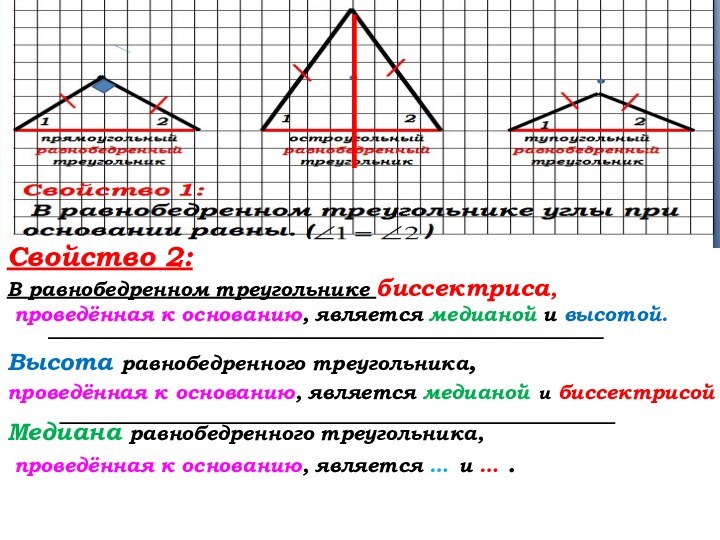
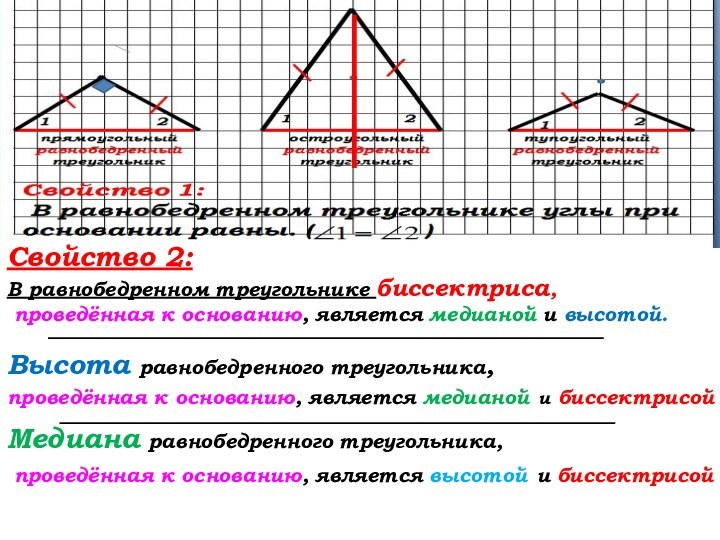
Свойство 2: (стр. 35)
В
А
С
В
А
С
В
А
С
D
1
2
В
А
С
D
1
2
В
А
С
D
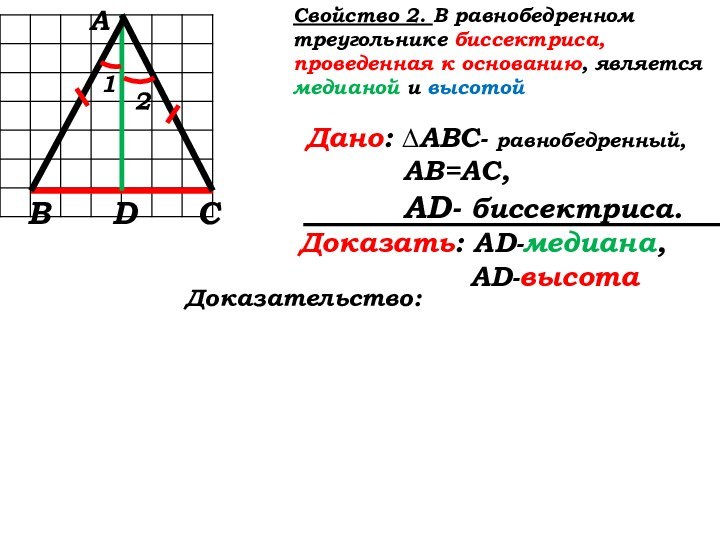
Доказательство:
1
2
В
А
С
D
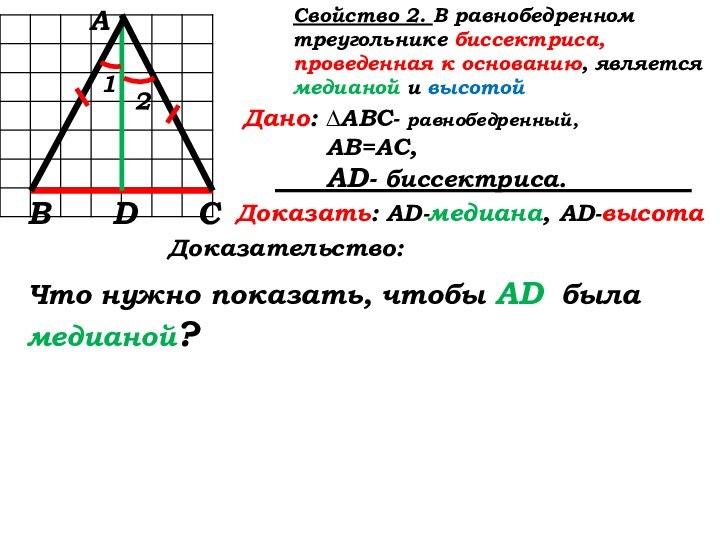
Доказательство:
Что нужно показать, чтобы AD была медианой?
1
2
В
А
С
D
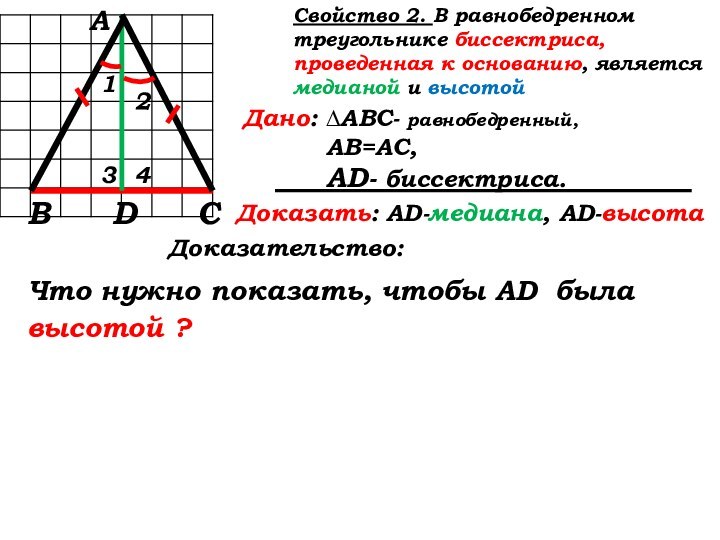
Доказательство:
Что нужно показать, чтобы AD была высотой ?
1
2
3
4
В
А
С
D
Доказательство:
В какие треугольники как элементы входят отрезки BD и DC, ?
1
2
3
4
В
А
С
D
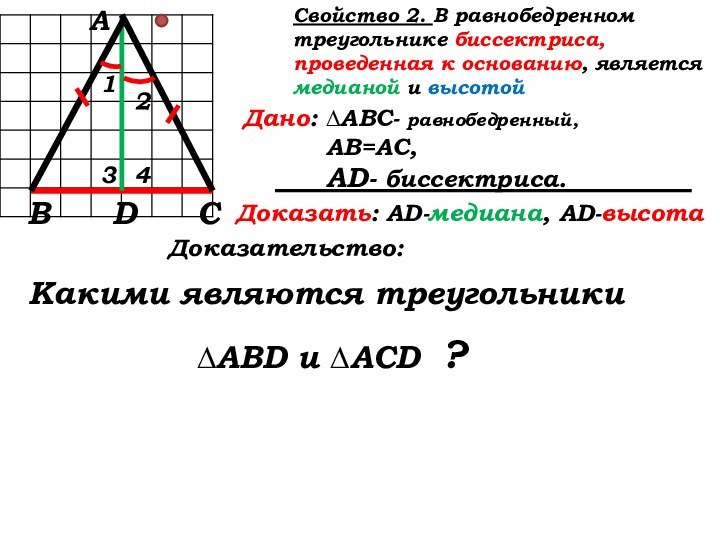
Доказательство:
Какими являются треугольники
1
2
3
4
∆ABD и ∆ACD ?
В
А
С
D
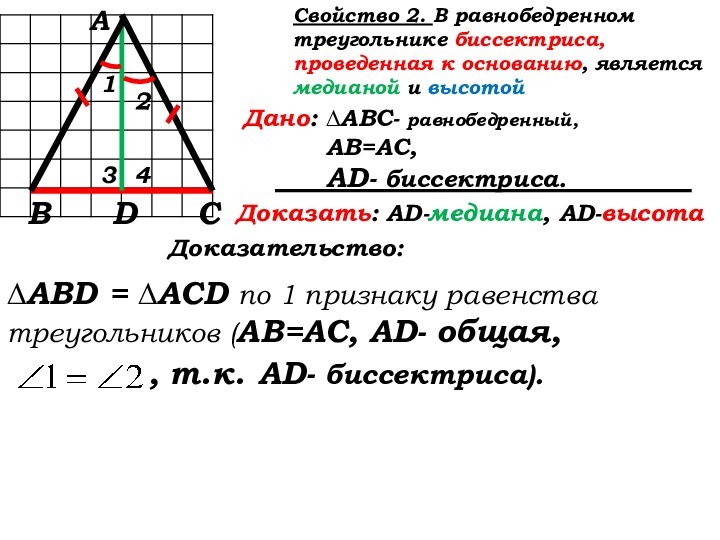
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая,
, т.к. AD- биссектриса).
В
А
С
D
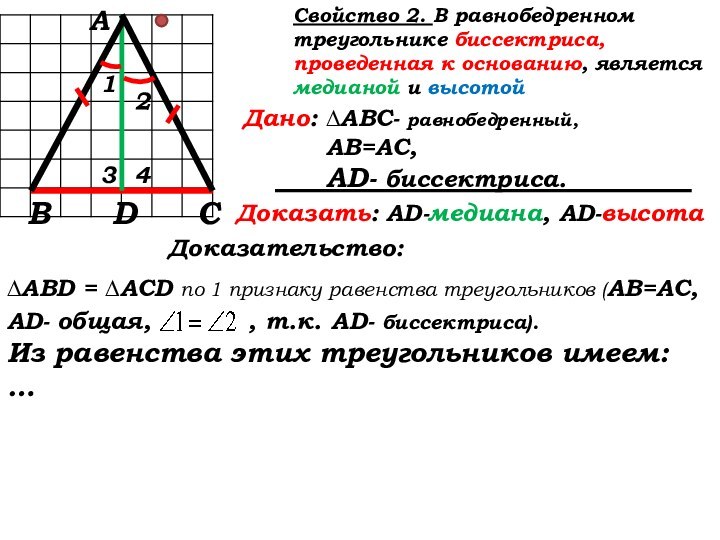
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
…
В
А
С
D
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC
В
А
С
D
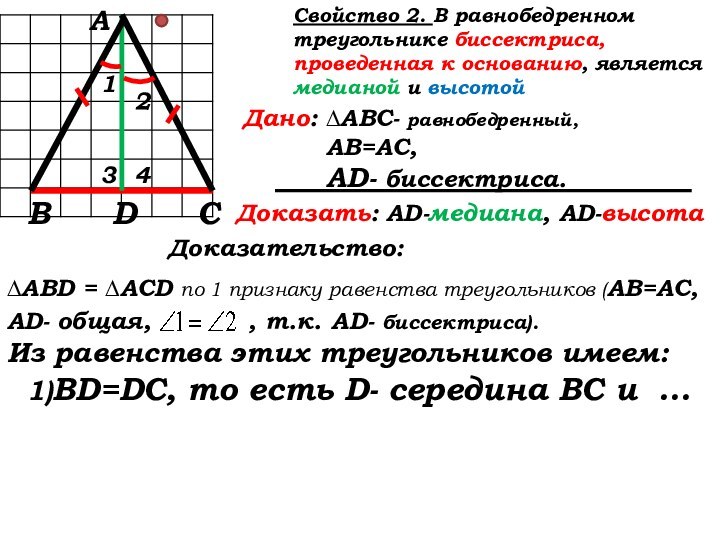
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1)BD=DC, то есть D- середина ВС и …
В
А
С
D
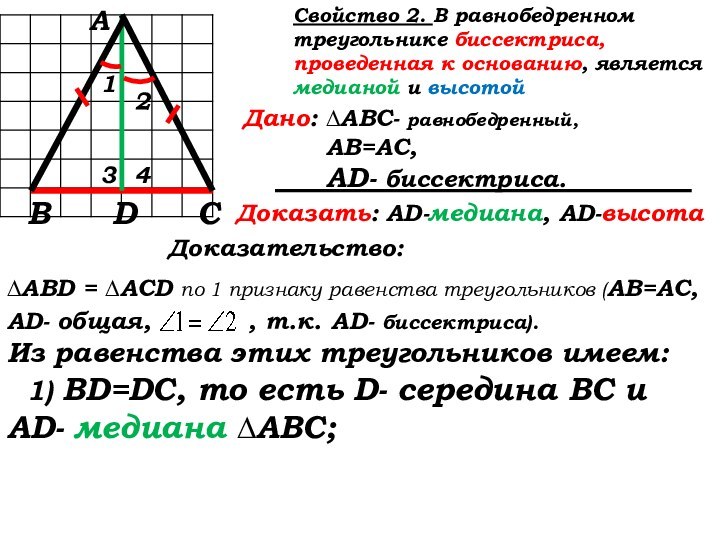
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и
AD- медиана ∆АВС;
В
А
С
D
Доказательство:
1
2
3
4
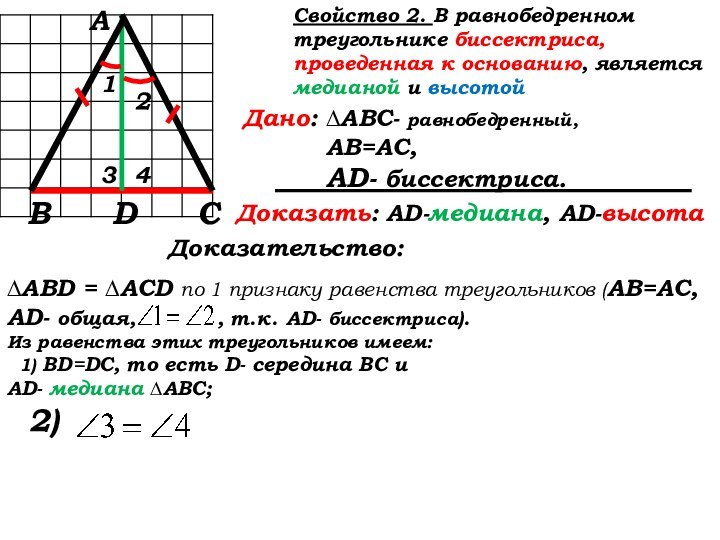
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и
AD- медиана ∆АВС;
2)
В
А
С
D
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и
AD- медиана ∆АВС;
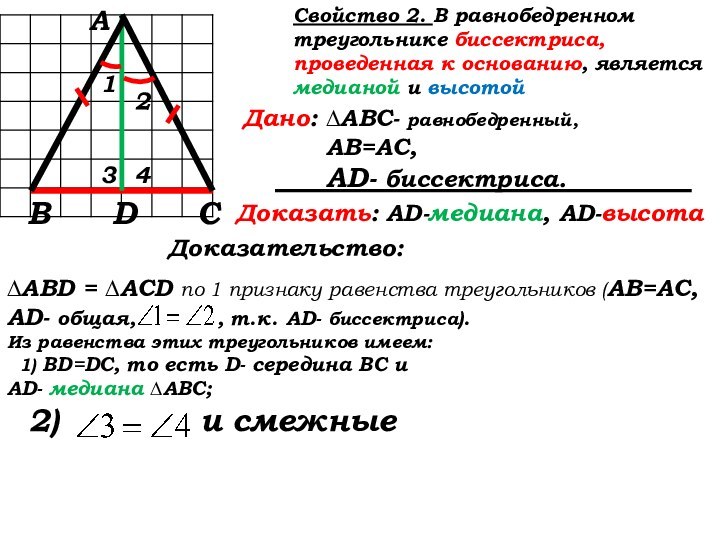
2) и …
В
А
С
D
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и
AD- медиана ∆АВС;
2) и смежные
В
А
С
D
Доказательство:
1
2
3
4
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и
AD- медиана ∆АВС;
2) и смежные, поэтому -…
В
А
С
D
Доказательство:
1
2
3
4
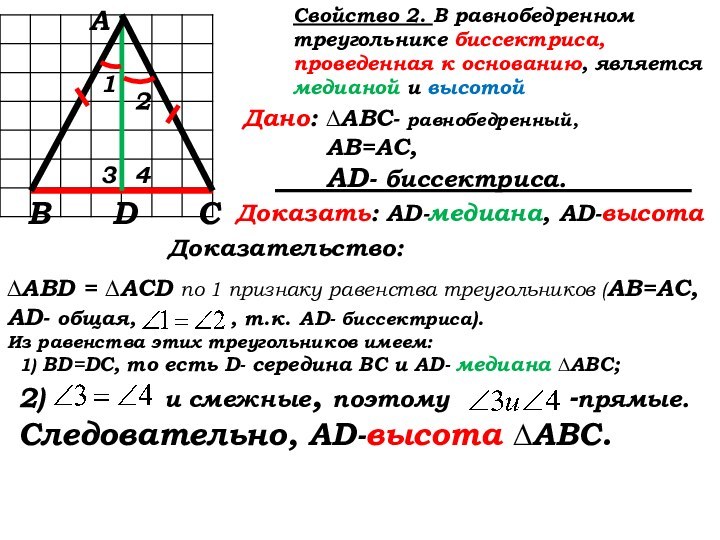
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и AD- медиана ∆АВС;
2) и смежные, поэтому -прямые.
Следовательно, AD-высота ∆АВС.
В
А
С
D
Доказательство:
1
2
3
4
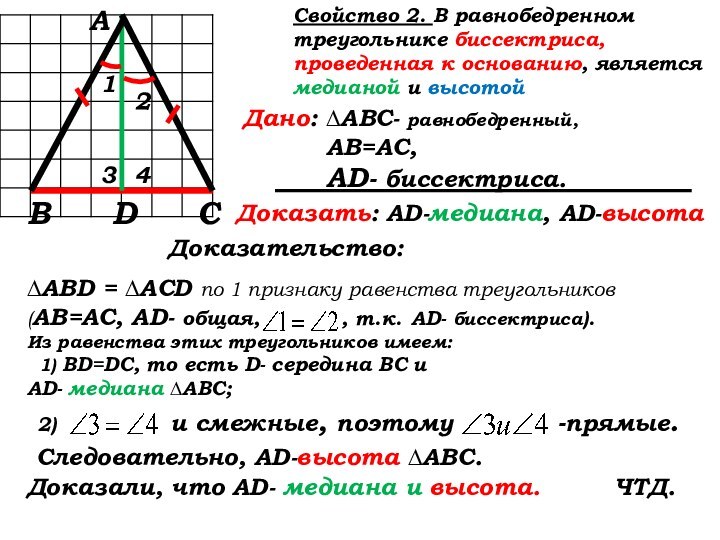
∆ABD = ∆ACD по 1 признаку равенства треугольников (АВ=АС, AD- общая, , т.к. AD- биссектриса).
Из равенства этих треугольников имеем:
1) BD=DC, то есть D- середина ВС и
AD- медиана ∆АВС;
2) и смежные, поэтому -прямые.
Следовательно, AD-высота ∆АВС.
Доказали, что AD- медиана и высота. ЧТД.