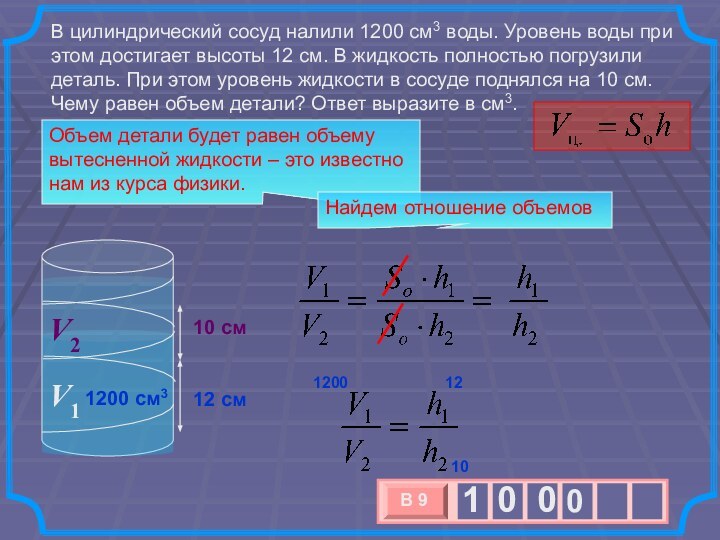
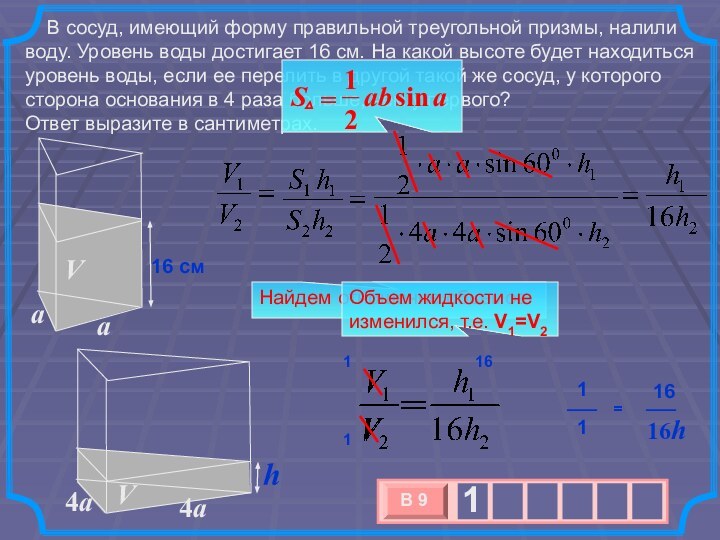
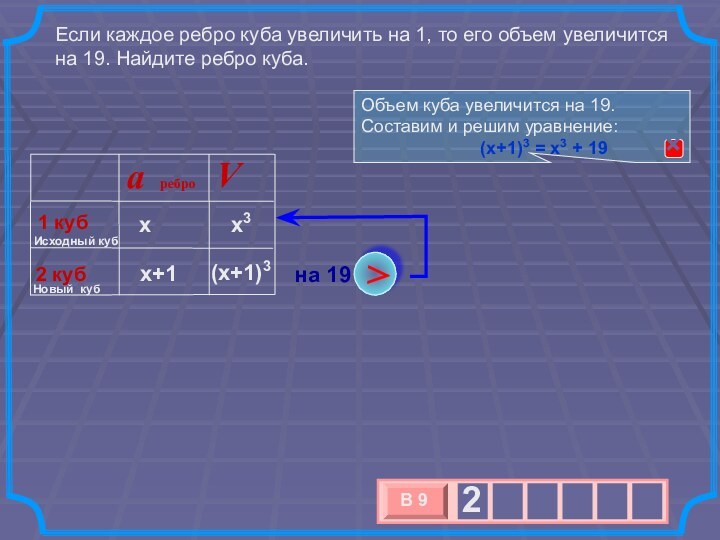
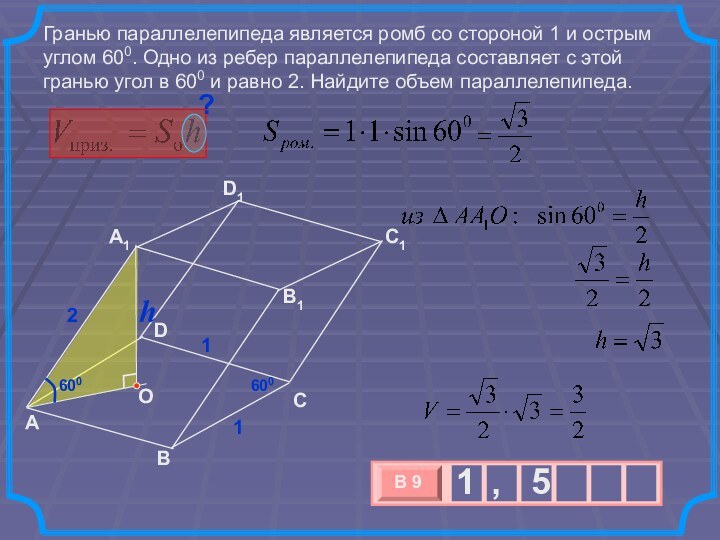
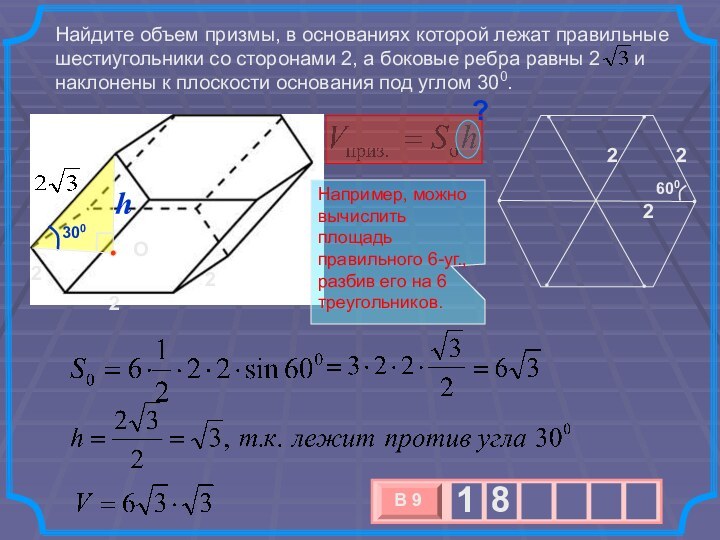
при этом достигает высоты 12 см. В жидкость полностью
погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см3.1200
12
10
Объем детали будет равен объему вытесненной жидкости – это известно нам из курса физики.
Найдем отношение объемов