- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к урок по геометрии в 8 классе на тему Площадь параллелограмма
Содержание
- 2. Для того чтобыусовершенствовать свой ум, надо больше
- 3. Историческая справка 365
- 4. Свойства параллелограмма?
- 5. Историческая справкаТермин «параллелограмм» греческого происхождения и был
- 6. Вопросы для повторения: Основные свойства площади?
- 7. А ВСДНМДано:АВСД – равнобедренная трапецияВН, СМ –
- 8. 2. Площадь прямоугольника АВСД равна 26 .
- 9. Площадь прямоугольного треугольникаАВС 1. Дано:.
- 10. Найдите площадь треугольника, изображенного на клетчатой бумаге
- 11. Найдите площадь треугольника, изображенного на клетчатой бумаге
- 12. Найдите площадь четырехугольника, изображенного на клетчатой бумаге
- 13. Тема урока:« Площадь параллелограмма».
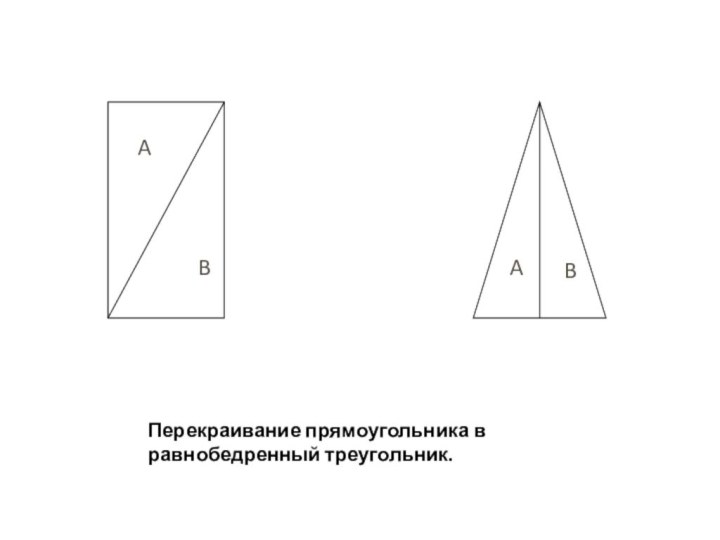
- 14. ABABПерекраивание прямоугольника в равнобедренный треугольник.
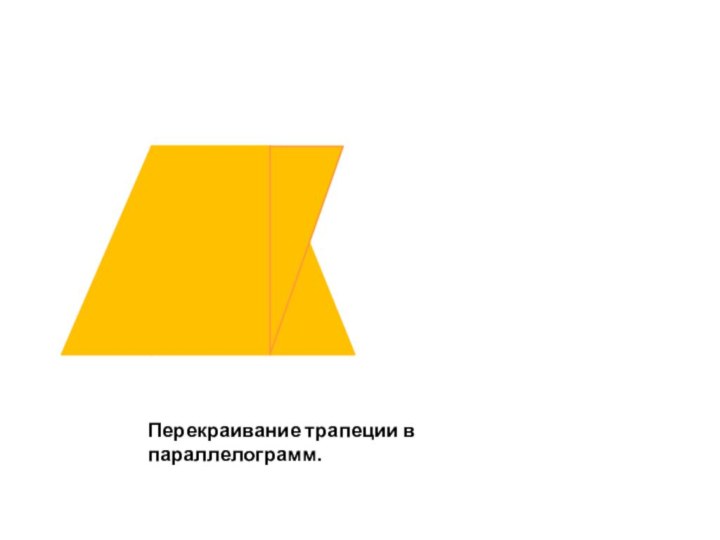
- 16. Перекраивание трапеции в параллелограмм.
- 17. Площадь параллелограмма Как найти
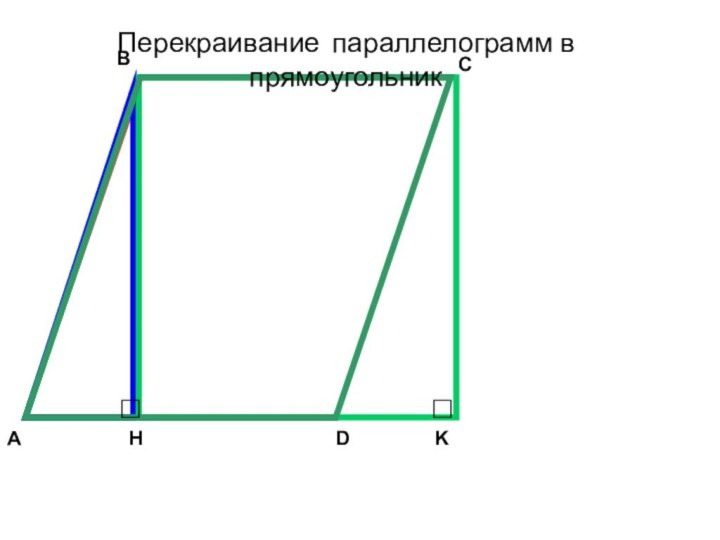
- 18. KABCDH Перекраивание параллелограмм в прямоугольник
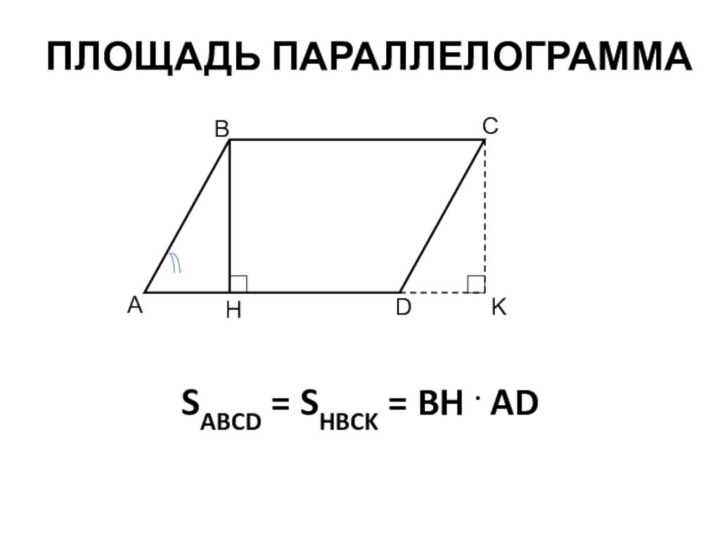
- 19. АВСDНKSABCD = SHBCK = BH . ADПлощадь параллелограмма
- 20. Итак, площадь параллелограмма…ABCDHAD – сторона параллелограмма (основание)ВН
- 22. Вывод формулы площади параллелограмма.Теорема:Площадь параллелограмма равна произведению
- 23. Домашнее задание: п 52 теорема о площади
- 24. Интересная задачаНачинаем «сдвигать» верхнее основание прямоугольника относительно
- 25. Скачать презентацию
- 26. Похожие презентации






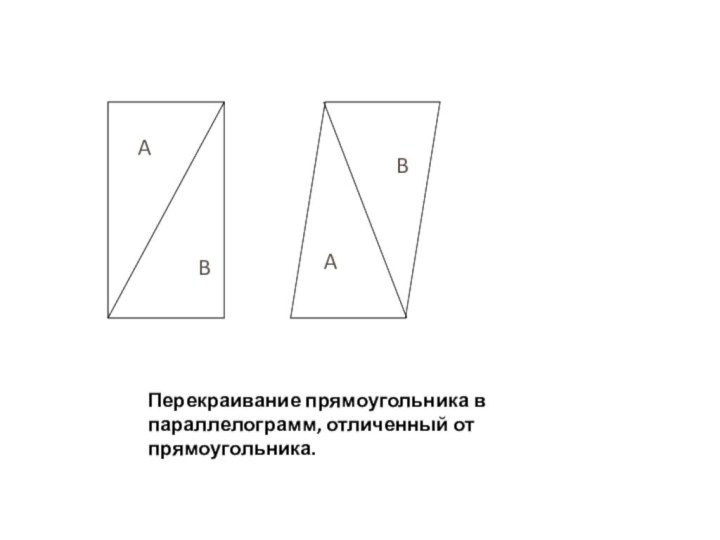





Слайд 3
Историческая справка
365 -
300 лет до н. э.
ЕВКЛИД
О жизни Евклида известно
очень мало. Главное его сочинение – труд по геометрии «Начала»: геометрия на плоскости;
учение о подобии;
арифметику;
квадратные уравнения;
стереометрию;
площади кругов и квадратов;
правильные многогранники.
?
Слайд 5
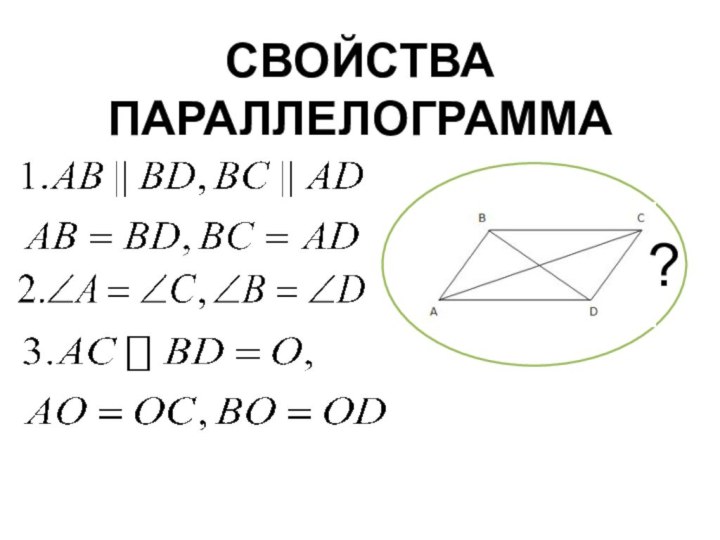
Историческая справка
Термин «параллелограмм» греческого происхождения и был введён
Евклидом. В «Началах» Евклида доказаны не все свойства параллелограмма,
а только первые два.
Слайд 6
Вопросы для повторения:
Основные свойства площади?
1.Равные
фигуры имеют одинаковую площадь.
2.Если многоугольник составлен из нескольких
многоугольников, то его площадь равна сумме площадей этих многоугольников.3.Площадь квадрата равна квадрату его стороны.
Слайд 7
А
В
С
Д
Н
М
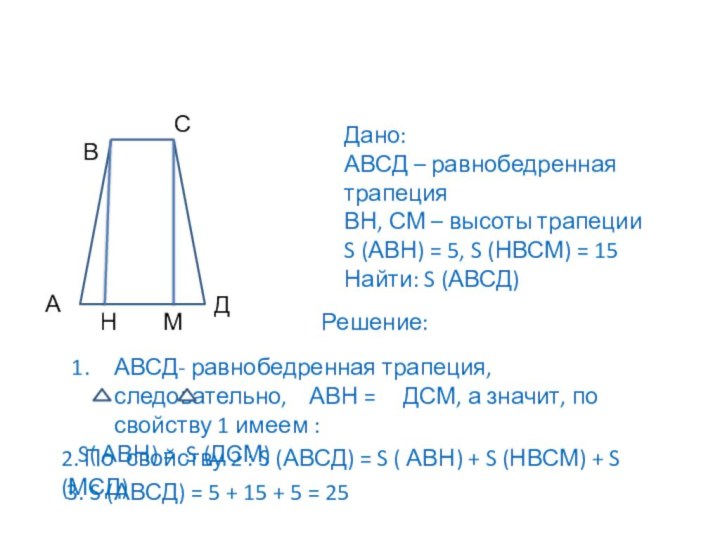
Дано:
АВСД – равнобедренная трапеция
ВН, СМ – высоты
трапеции
S (АВН) = 5, S (НВСМ) = 15
Найти: S
(АВСД)Решение:
АВСД- равнобедренная трапеция, следовательно, АВН = ДСМ, а значит, по свойству 1 имеем :
S( АВН) = S (ДСМ)
2. По свойству 2 : S (АВСД) = S ( АВН) + S (НВСМ) + S (МСД)
3. S (АВСД) = 5 + 15 + 5 = 25
Слайд 8 2. Площадь прямоугольника АВСД равна 26 . Найдите
площадь треугольника АВД.
А
В
С
Д
Решение:
1. Проведём диагональ ВД
2.
АВД = СДВ, сл- но, S ( АВД) = S ( ДСВ), а значит, S ( АВСД) = 2S ( АВД)
3. S ( АВД) = 26 : 2 = 13
Какой вывод вы можете сделать о нахождении площади прямоугольного треугольника?
Слайд 9
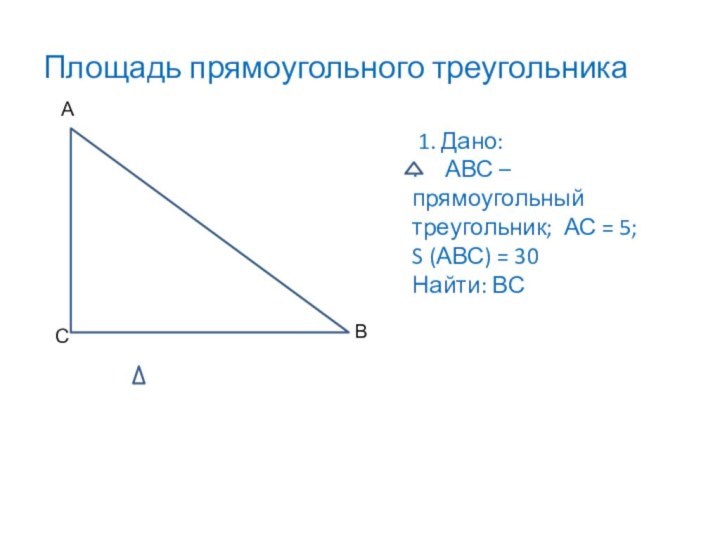
Площадь прямоугольного треугольника
А
В
С
1. Дано:
. АВС
– прямоугольный треугольник; АС = 5;
S (АВС) =
30Найти: ВС
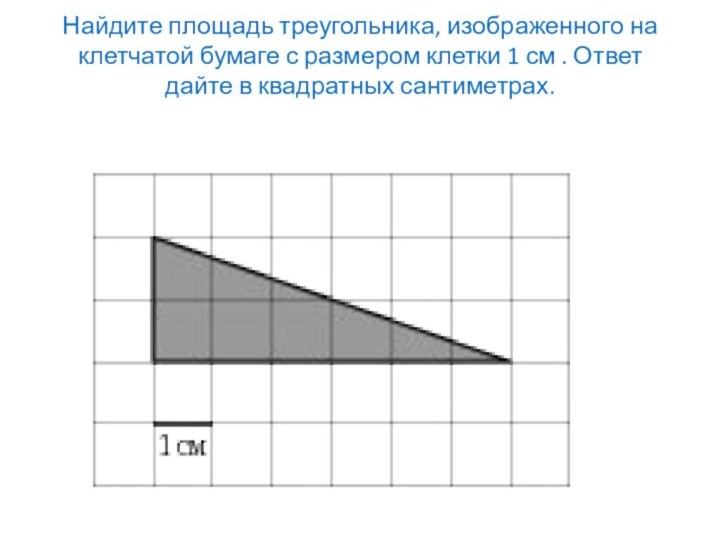
Слайд 10 Найдите площадь треугольника, изображенного на клетчатой бумаге с
размером клетки 1 см . Ответ дайте в квадратных
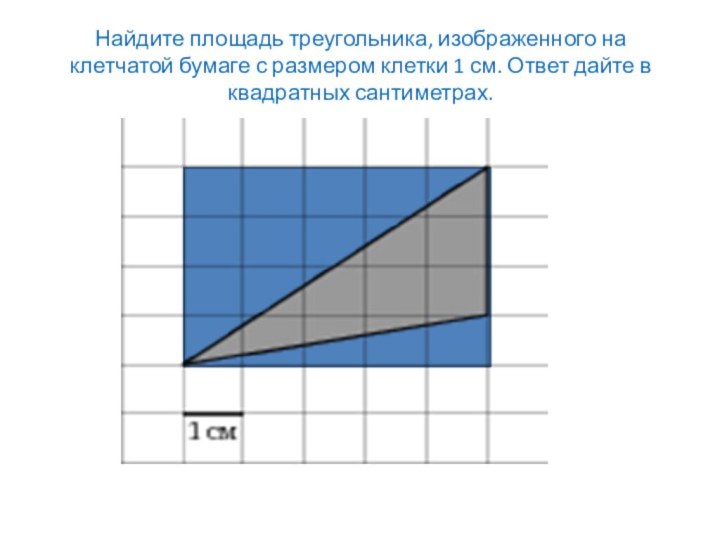
сантиметрах.Слайд 11 Найдите площадь треугольника, изображенного на клетчатой бумаге с
размером клетки 1 см. Ответ дайте в квадратных сантиметрах.
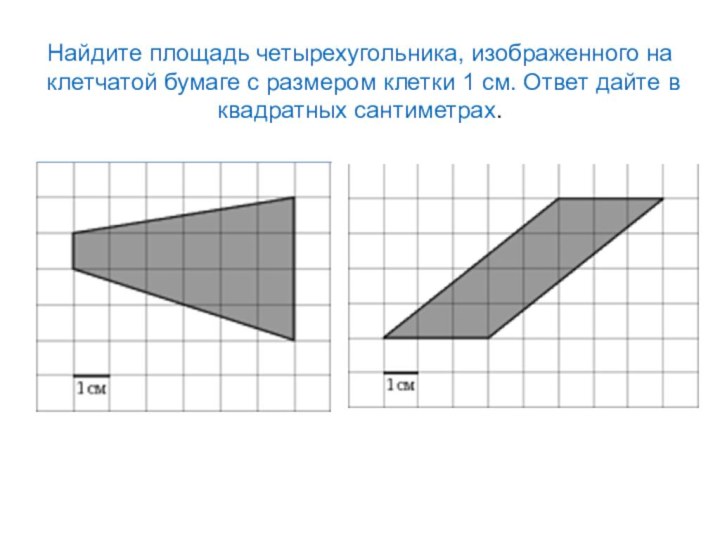
Слайд 12 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с
размером клетки 1 см. Ответ дайте в квадратных сантиметрах.
Слайд 17
Площадь параллелограмма
Как найти площадь параллелограмма
, если он изображён на листе бумаги без клеточек?
Как
, используя свойства площадей и решённые задачи, можно вывести формулу площади параллелограмма?
Слайд 20
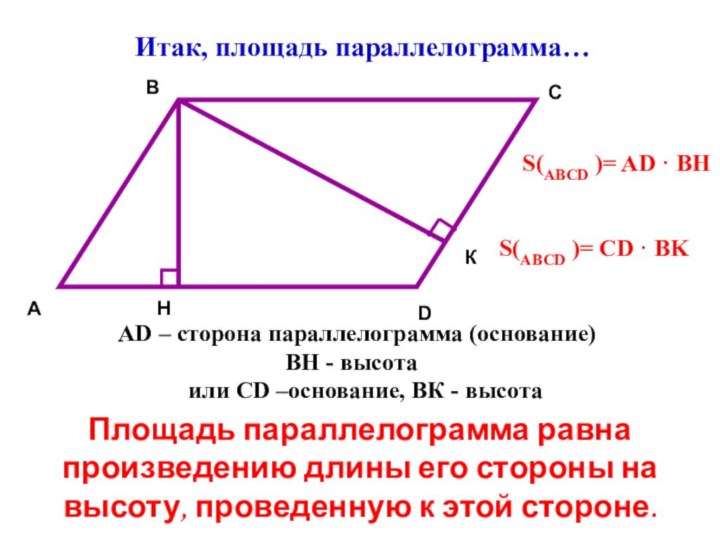
Итак, площадь параллелограмма…
A
B
C
D
H
AD – сторона параллелограмма (основание)
ВН -
высота
Площадь параллелограмма равна произведению длины его стороны на высоту,
проведенную к этой стороне.К
или CD –основание, ВК - высота
S(АВСD )= AD · BH
S(АВСD )= CD · BK
Слайд 22
Вывод формулы площади параллелограмма.
Теорема:
Площадь параллелограмма равна произведению длины
стороны параллелограмма на высоту, проведенную к этой стороне.
A
B
C
D
H
Дано: АВСD
– параллелограмм, ВН – высотаДоказать: S(ABCD )= AD · BH
Доказательство: проведем высоту параллелограмма – отрезок СК и рассмотрим треугольники АВН и DСК.
K
Они прямоугольные и равны по гипотенузе и острому углу (гипотенузы АВ и СD равны как противоположные стороны параллелограмма, а углы BAH и CDK равны как соответственные углы при пересечении параллельных прямых АВ CD секущей AD ). Значит, площади треугольников равны.
S(ABCD)=S(ABH)+S(HBCD)
S(HBCK ) = S(HBCD)+S(DCK)
, S(ABH)=S(DCK)
S(ABCD)=S(HBCK)
S(HBCK )= HK · BH, так как НВСК – прямоугольник;
так как AD = BC = HK, то S(ABCD )= HK · BH = AD · BH . Итак, S(ABCD )= AD · BH .
Теорема доказана.
Слайд 23
Домашнее задание: п 52 теорема о площади параллелограмма.
Найти
другие формулы, которые позволят также вычислить площадь параллелограмма.
Открытый банк
задач http://mathege.ru/or/ege/Main1). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
2). Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
3) №459(б, г)
Слайд 24
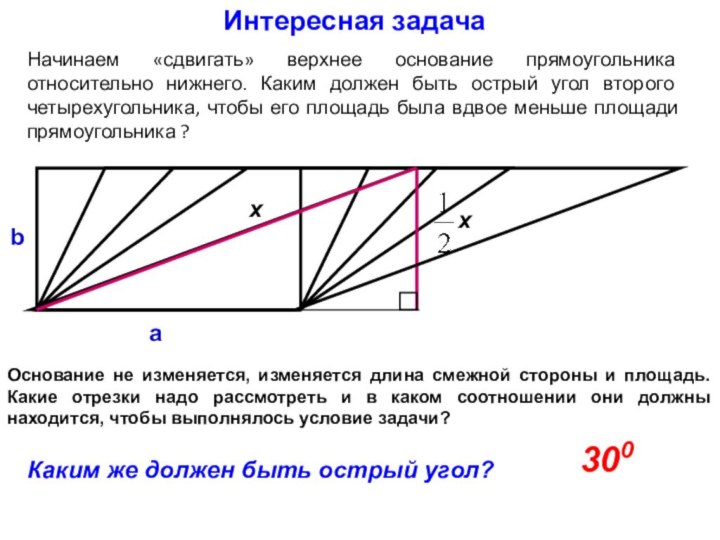
Интересная задача
Начинаем «сдвигать» верхнее основание прямоугольника относительно нижнего.
Каким должен быть острый угол второго четырехугольника, чтобы его
площадь была вдвое меньше площади прямоугольника ?Основание не изменяется, изменяется длина смежной стороны и площадь. Какие отрезки надо рассмотреть и в каком соотношении они должны находится, чтобы выполнялось условие задачи?
х
х
Каким же должен быть острый угол?
300
а
b