хордой, проходящей через точку касания, измеряется половиной заключенной в
нем дугиА
В
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




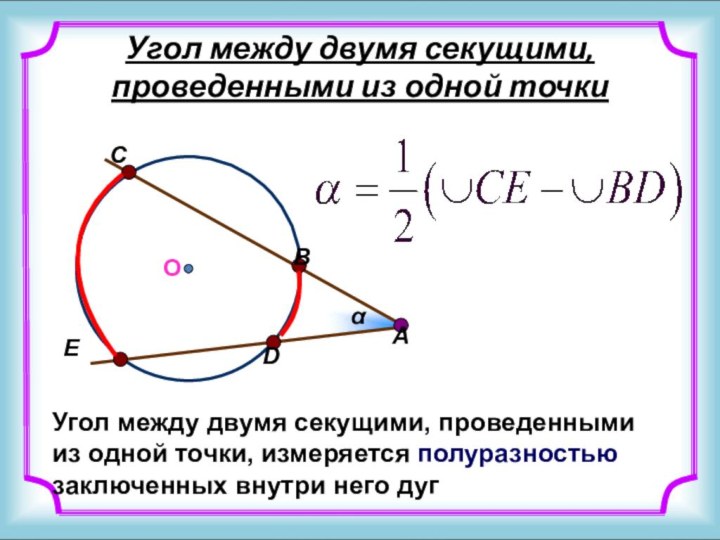



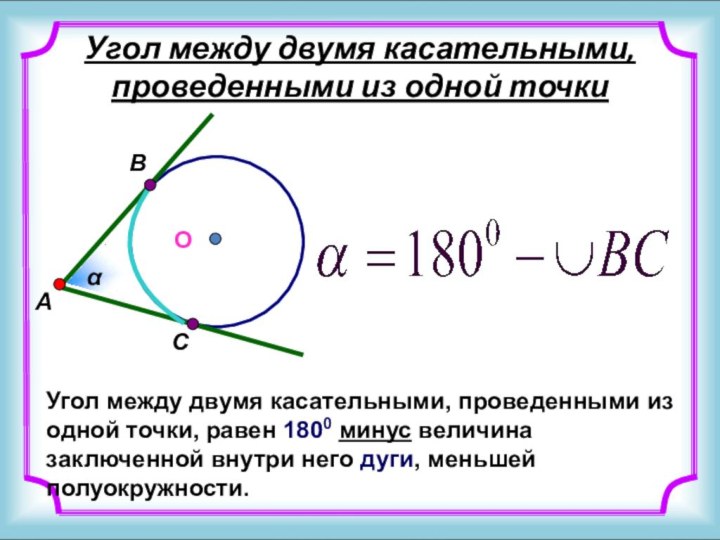










А
В
Ответ: 40о
О
α
А
B
C
D
E
Ответ: 35о
О
α
A
B
C
D
Ответ: 40о
О
α
A
B
C
20º =½· 40º
Можно построить окружность с центром в точке D, проходящую через остальные три вершины четырехугольника С; В и D
∠ BCA и ∠ BДA опираются на отрезок ВА и лежат от него по одну сторону
Из Δ APD
∠ APD = 180º – 40º – 35º = 105º.
Углы между диагоналями равны
105º и 75º
Ответ: 105°; 75°
∆ ACD - равнобедренный
В выпуклом четырехугольнике ABCD ∠ BCA = 20º,
∠ BAC = 35º, ∠ BDС = 70º, ∠ BDA = 40º. Найдите углы между диагоналями этого четырехугольника.
CD = DA как радиусы одной окружности
ADB = ½ АСВ и углы «опираются» на один отрезок – АВ и лежат от него по одну сторону
Можно построить окружность с центром в точке С и R = ВС = АС = 5
CD = 5
∆ACD - равнобедренный
Проведём высоту СК
CК = 4
Ответ: 22
3
3