Презентация на тему Площадь трапеции.

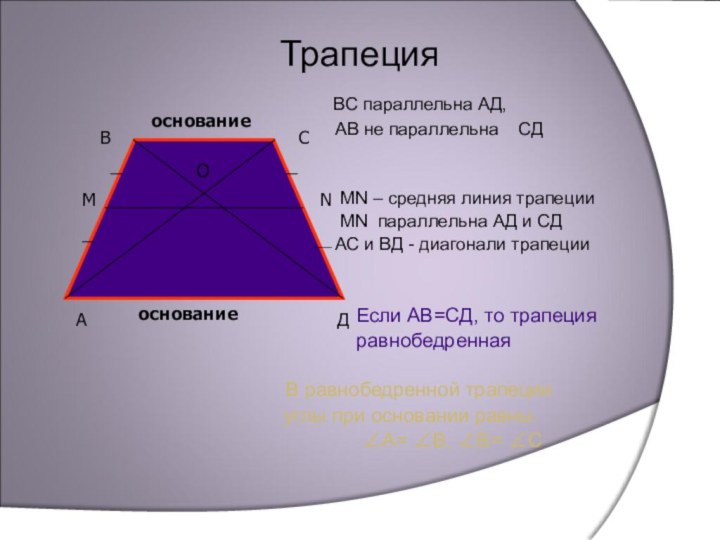
ВС параллельна АД,
АВ не параллельна СД


МN – средняя линия трапеции
MN параллельна АД и СД
АС и ВД - диагонали трапеции


Если АВ=СД, то трапеция
равнобедренная

В равнобедренной трапеции
углы при основании равны.
∠А= ∠В, ∠В= ∠С

А

В

С

Д

О

основание

основание

M

N

из любой точки одного из оснований к

прямой, содержащей другое основание .

A

B

С

D

H

H1

На рисунке BH и DH1 - высоты трапеции.

её оснований на высоту

Дано: ABCD-трапеция
AD и BC – основания трапеции
BH – высота трапеции
Доказать: Sтр= 1/2(AD+BC) BH
Доказательство:
1. Е – середина основания AD, AE=ED
2. Проведём BE и CE
3. Получаем треугольники: ABE, BEC, CDE
По свойству площадей площадь трапеции равна сумме площадей трёх треугольников.
SABCD=SABE+SBEC+SCED=1/2AE BH+1/2ED BH+1/2BC BH=
=1/2 (AE+ED+BC)BH= ½ (AD+BC) BH

A

B

C

D

H

E

Доказательство:

1. Сложим две одинаковые трапеции
так, чтобы получился параллелограмм

Sтр= ½ Sпар = 1/2 (a+b) h

Sтр= ½ (a+b)h, где
а и b- основания трапеции
h – высота трапеции

a

b

a

b

h

s=sпар+sтр=
=bh+1/2(а-b)h=1/2(a+b)h

а

в

h

a-b

основания трапеции
∠Д=30º, АВ=2см, СД= 10см,

ДА=8см
Найти: Sтр

Решение.

1. Sтр=1/2 (CД+АВ) АН

2. АН находим из прямоугольного ∆АДН.



3. Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы АН=8:2=4см
Sтр= ½ (АВ+СД) АН = ½ ( 2+10) 4 = 24 см²
Ответ: 24 см²

С

А

Д

В

H

30

2

8

10

АВ=ВС=6см, ∠С=135º
Найти: Sтр
Решение.
1. Проведём СН АД
2. Рассмотрим прямоугольный ∆СНД
3. ∠НСД=135º - 90º = 45º
4. ∠СДН = 90º - 45º = 45º
5. ∆СНД – прямоугольный и равнобедренный. СН=НД=6см
АД=АН+НД = 6+6 = 12 см
Sтр=1/2 (АД+ВС) АН= ½ (12+6) 6=54 см²
Ответ: 54 см²

А

С

В

Д

6

6

Н