- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Исследовательская работа по золотому сечению
Содержание
- 2. МИРНЫЙ АТОМОСВОЕНИЕ КОСМОСА
- 3. Авария на АЭС Фукусима-1. ЯпонияВзрыв на буровой платформе Deepwater Horizon.Мексиканский залив возле штата Луизиана
- 5. АкТУАЛЬНОСТЬАктуальность данной работы мы видим в теме
- 6. ТемаИсследование связи золотого сечения с числами Фибоначчи и теоремой Пифагора
- 7. Цель работыОпределить и доказать связь золотого сечения с числами Фибоначчи и, как следствие, с теоремой Пифагора
- 8. Объект исследования Задачи, связанные с золотым сечением
- 9. Предмет исследованияскрытые «золотые» свойства геометрических фигур и ряда Фибоначчи.
- 10. ГипотезаЯвляется ли известное со времён античности золотое
- 11. Задачи:Изучить понятие золотого сечения. Исследовать математические задачи, связанные
- 12. Методы исследования:ТеоретическийПрактический
- 14. Свойства золотого сечения описываются уравнением: x2 – x – 1 = 0.
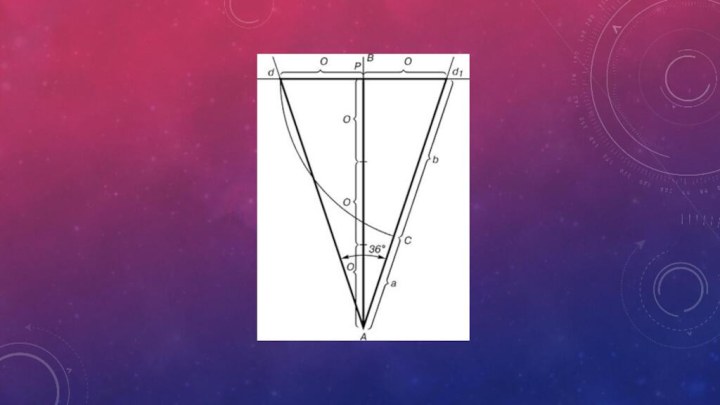
- 15. Практическое знакомство с золотым сечением начинают с
- 18. Связь золотого сечения с числами фибоначчиПоследовательность Фибоначчи
- 19. На практике это выглядит так:
- 20. 0, 1, 1, 2, 3, 5, 8,
- 21. Значения гипотенуз, соответствующих прямоугольных треугольников, исходя из чисел Фибоначчи
- 22. Скачать презентацию
- 23. Похожие презентации
МИРНЫЙ АТОМОСВОЕНИЕ КОСМОСА





















Слайд 5
АкТУАЛЬНОСТЬ
Актуальность данной работы мы видим в теме перехода
объективных законов прекрасного в их математическое обличие, что является
следствием гуманитаризации научно-технических знаний.
Слайд 7
Цель работы
Определить и доказать связь золотого сечения с
числами Фибоначчи и, как следствие, с теоремой Пифагора
Слайд 10
Гипотеза
Является ли известное со времён античности золотое сечение
ничем иным, как конкретной разновидностью единого морфологического принципа симметрии.
Слайд 11
Задачи:
Изучить понятие золотого сечения.
Исследовать математические задачи, связанные с
золотым сечением и числами Фибоначчи.
Проанализировать полученную информацию и доказать
связь золотого сечения, чисел Фибоначчи.Слайд 15 Практическое знакомство с золотым сечением начинают с деления
отрезка прямой в золотой пропорции с помощью циркуля и
линейки.AЕ = 0,618; BE = 0,382
Слайд 18
Связь золотого сечения с числами фибоначчи
Последовательность Фибоначчи —
это числовой ряд, в котором каждый последующий член представляет
собой сумму двух предыдущих:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
каждое последующее число в числовом ряду приблизительно в 1.618 раз больше предыдущего, а каждое предыдущее составляет приблизительно 0.618 от следующего.
Отношение через одно число составляет 0.382, а обратное ему число = 2.618. За исключением нескольких первых чисел последовательности.
Слайд 20 0, 1, 1, 2, 3, 5, 8, 13,
21, 34, 55, 89, 144, 233, 377, 610, 987,
1597, 2584, 4181, 6765, 1094612+12=2
12+22=5
22+32=13
32+52=34
52+82=89
82+132=233





























