- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Средняя линия трапеции
Содержание
- 2. Трапеция – это четырехугольник , у которого
- 3. Определение средней линии трапецииСредней линией трапеции называется
- 4. Теорема о средней линии трапецииADBCДано: ABCD, BC
- 5. Теорема о средней линии трапецииADBCДоказательство:Е1. Дополнительное построение 1)
- 6. Теорема о средней линии трапецииADBCДоказательство:Е4. ΔECD :
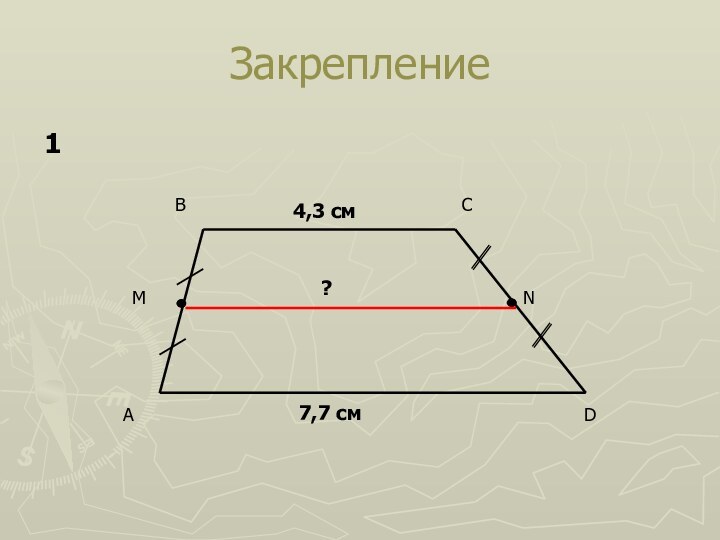
- 7. Закрепление4,3 см7,7 см?1
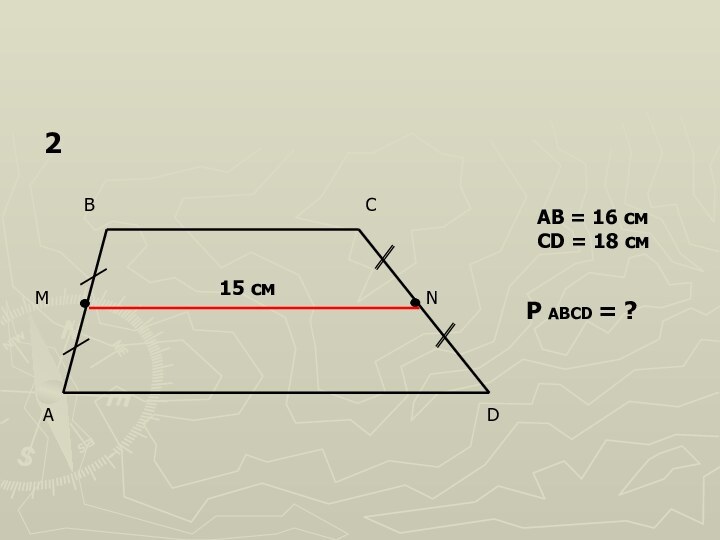
- 8. 15 смAB = 16 смCD = 18 смP ABCD = ?2
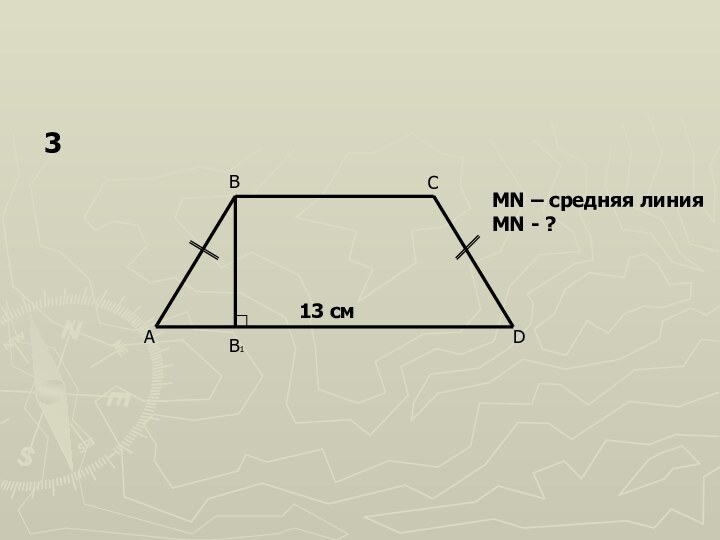
- 9. ABCDB113 смMN – средняя линияMN - ?3
- 10. Самостоятельная работа5 см№1Решение:BC = Х смAD =
- 11. Самостоятельная работаADBC№2Решение:Sabcd = CE*(BC+AD)/2 CE = CD*cos(30°)
- 12. Скачать презентацию
- 13. Похожие презентации
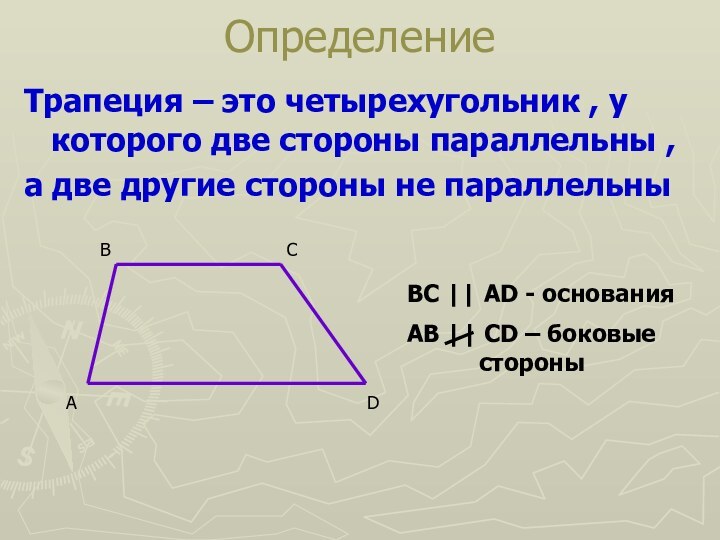
Трапеция – это четырехугольник , у которого две стороны параллельны ,а две другие стороны не параллельныОпределение



Слайд 3
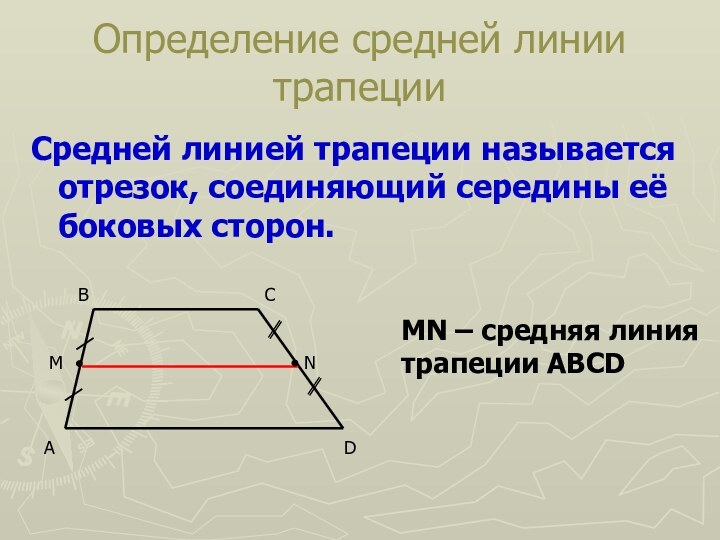
Определение средней линии трапеции
Средней линией трапеции называется отрезок,
соединяющий середины её боковых сторон.
MN – средняя линия трапеции
ABCD
Слайд 4
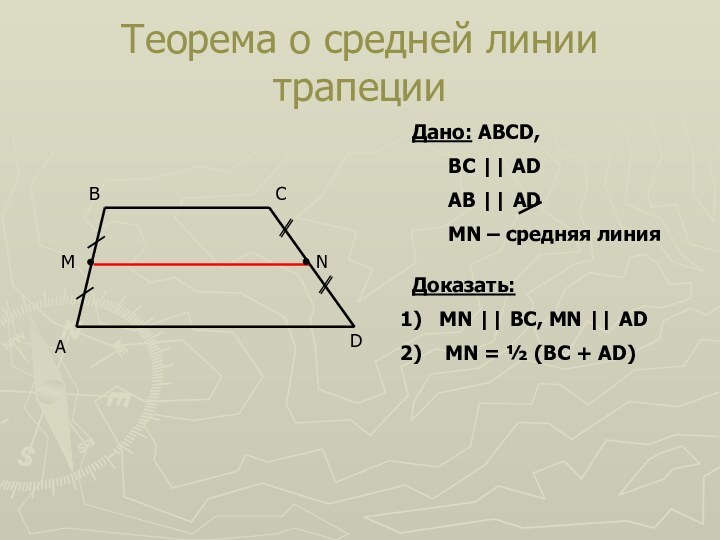
Теорема о средней линии трапеции
A
D
B
C
Дано: ABCD,
BC ||
AD
AB || AD
MN – средняя линия
Доказать:
MN || BC, MN
|| ADMN = ½ (BC + AD)
Слайд 5
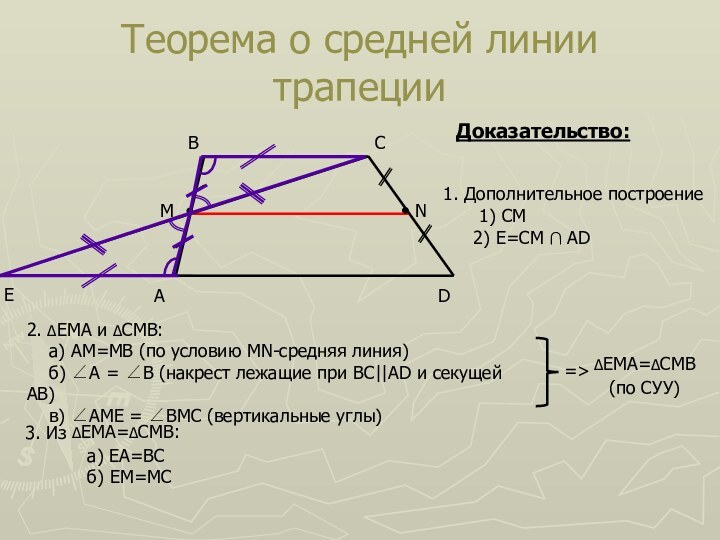
Теорема о средней линии трапеции
A
D
B
C
Доказательство:
Е
1. Дополнительное построение
1) CM
2.
ΔEMA и ΔCMB:
а) AM=MB (по условию MN-средняя
линия)б) ∠A = ∠B (накрест лежащие при BC||AD и секущей AB)
в) ∠AME = ∠BMC (вертикальные углы)
2) E=CM ∩ AD
а) EA=BC
б) EM=MC
Слайд 6
Теорема о средней линии трапеции
A
D
B
C
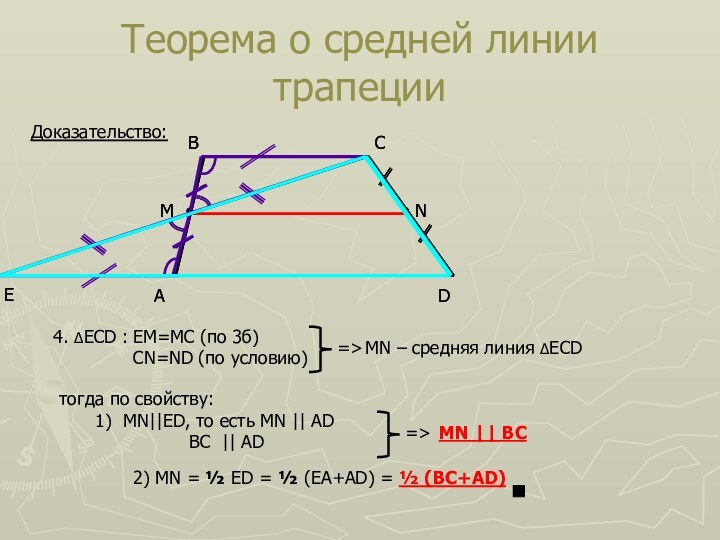
Доказательство:
Е
4. ΔECD :
EM=MC
(по 3б)
CN=ND (по условию)
тогда по свойству:
1) MN||ED, то есть
MN || ADBC || AD
2) MN = ½ ED = ½ (EA+AD) = ½ (BC+AD)
A
D
B
C
Е
Слайд 10
Самостоятельная работа
5 см
№1
Решение:
BC = Х см
AD = 1.5X
см
BC+AD = 10 см
X + 1.5X = 10
X =
4BC = 4 см
AD = 6 см
Слайд 11
Самостоятельная работа
A
D
B
C
№2
Решение:
Sabcd = CE*(BC+AD)/2
CE = CD*cos(30°) =
CD*sin(60°)
CE = 20*(√3) /2 = 10 *(√3)
Sabcd =
14 * 10 *(√3) = 140*(√3) 20 см
E
60°
30°





























