- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сумма углов треугольника
Содержание
- 2. Задание 1.Постройте треугольник с углами 60,90 и 45градусов или 90,120,30 градусов.
- 3. Задание 2.Указание к работе1. Постройте в тетради
- 4. Тема урока: «Сумма углов треугольника».
- 5. Цель урока:Выяснить: - Чему равна сумма углов любого треугольника.
- 6. Виды углов1234
- 7. Рассмотрим рисунокаbс1234d5
- 8. Практическая работа.Возьмите бумажный треугольник, лежащий у каждого
- 9. Сумма углов треугольника равна Теорема
- 10. Рассмотрим произвольный треугольник АВС Дано: ∆АВСДок-ть: ∠ А + ∠ В + ∠ С= 1800
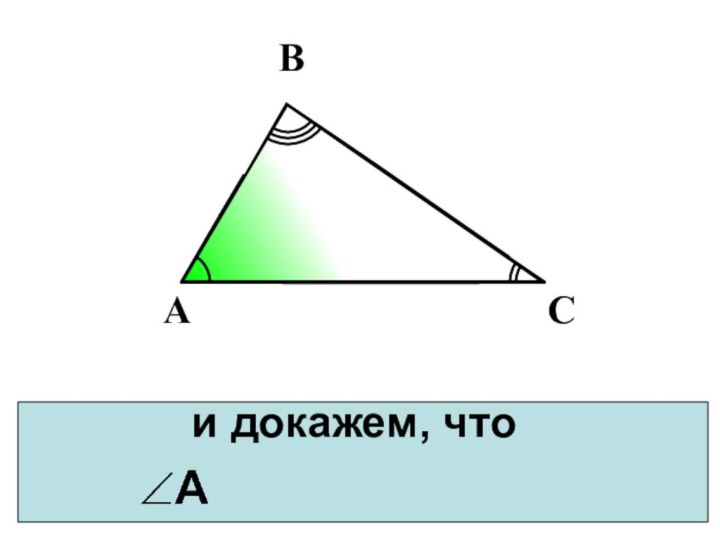
- 11. и докажем, что АВС
- 12. и докажем, что АВС
- 13. и докажем, что АВС
- 14. и докажем, что АВС
- 15. Проведем через вершину В прямую , параллельную стороне АС АСВС
- 16. Углы 1 и 4 являются накрест лежащими
- 17. А углы 3 и 5 являются накрест
- 18. Поэтому 4 = 1, 5 = 3 АС3В541С
- 19. Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т.е. АС2СВ45
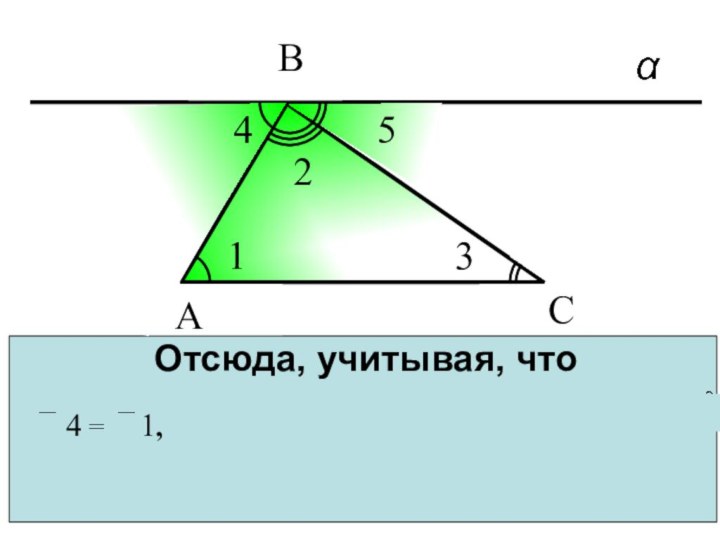
- 20. Отсюда, учитывая, что получаем илиА2С513В4 4 = 1,
- 21. Отсюда, учитывая, что получаем илиА2СВ1354
- 22. Теорема доказана
- 23. Примерный план доказательства
- 25. Историческая справкаДоказательство данного факта, изложенное в современных
- 26. Великий ученый Пифагор родился около
- 27. ВАСЕ21345? Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.
- 28. Устная работа: Найдите углы треугольников80º70º?ВАС А=30º
- 29. LКML=45º
- 30. NPRN=50ºR=50º
- 31. Существует ли треугольник с углами:
- 32. Работа с учебником. Стр.71 №223 а)№228 а)
- 33. Практическое применение знаний. Свойство
- 34. Итог урока. Сегодня
- 35. Домашнее заданиеП.30, №223(б), №228(в).Другой способ доказательства теоремы о сумме углов треугольника.
- 37. Скачать презентацию
- 38. Похожие презентации
Задание 1.Постройте треугольник с углами 60,90 и 45градусов или 90,120,30 градусов.
































Слайд 3
Задание 2.
Указание к работе
1. Постройте в тетради произвольный
треугольник АВС.
2. Измерьте градусные меры углов треугольника.
3.Запишите в
тетрадь:∠ А =…, ∠ В =…, ∠ С=…
4. Найдите сумму углов треугольника
∠ А + ∠ В + ∠ С=…
5.Сравните полученные результаты.
6.Попробуйте определить тему нашего урока.
Слайд 8
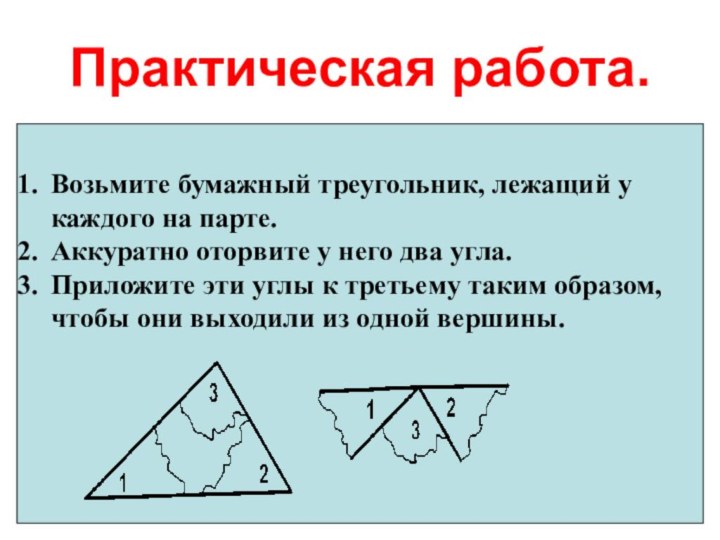
Практическая работа.
Возьмите бумажный треугольник, лежащий у каждого на
парте.
Аккуратно оторвите у него два угла.
Приложите эти углы к
третьему таким образом, чтобы они выходили из одной вершины.
Слайд 16
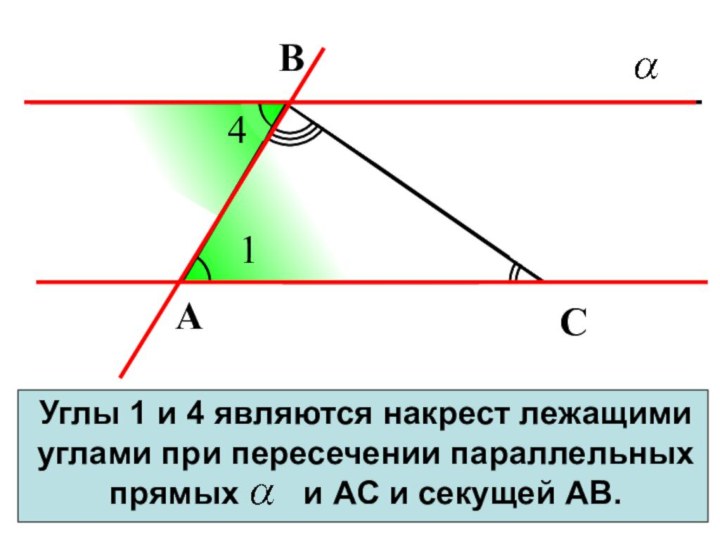
Углы 1 и 4 являются накрест лежащими углами
при пересечении параллельных прямых и АС
и секущей АВ.А
С
В
1
4
С
Слайд 17
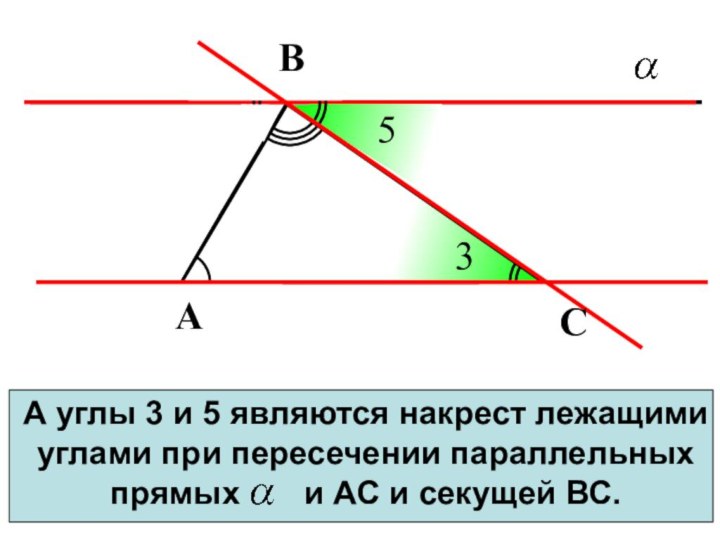
А углы 3 и 5 являются накрест лежащими
углами при пересечении параллельных прямых и
АС и секущей ВС.А
С
В
С
5
3
Слайд 25
Историческая справка
Доказательство данного факта, изложенное в современных учебниках,
содержалось ещё в комментарии к «Началам» Евклида древнегреческого учёного
Прокла (V в.н.э.) Прокл утверждает, что согласно Евдему Родосскому, это доказательство было открыто ещё пифагорейцами(Vв.до н.э.).





























