- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрические вариации на пчелиную тему.
Содержание
- 2. Основополагающий вопрос Чему можно удивляться глядя на мир?
- 3. Пчёлы – удивительные творения природы. Свои геометрические способности они проявляют при построении сот.
- 4. Геометрические способности пчел проявляются
- 5. Выполняя несложные расчеты, убеждаемся, что такими многоугольниками
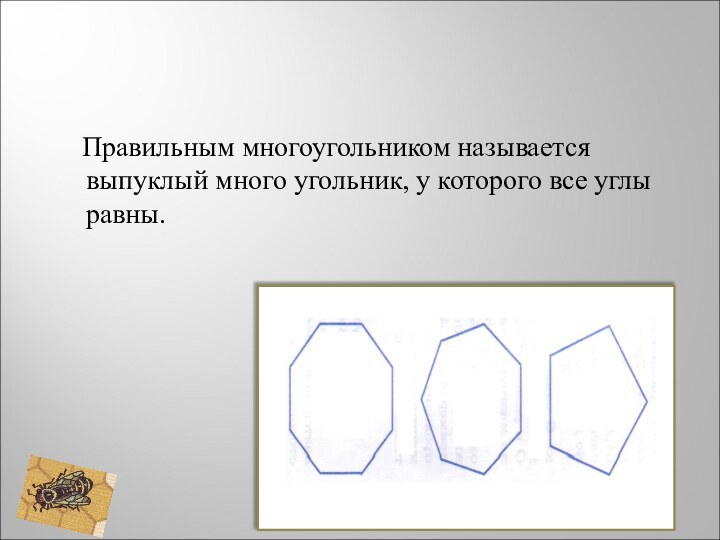
- 6. Правильным многоугольником называется выпуклый много угольник, у которого все углы равны.
- 7. Почему пчелы выбрали именно шестиугольник?Чтобы ответить на
- 8. Для того чтобы выяснить, почему пчела строит
- 9. Даны три равновеликие друг другу
- 11. Действительно, сумма внутренних углов выпуклого
- 12. Тогда (n-2)*180°/n*k=360°. Отсюда k=2n/(n-2).Если n=3, то k=6,
- 13. Теперь рассуждаем следующим образом:2/(n-2)>2, так как внутренней
- 14. Как не согласиться с
- 15. Паркеты с древних времён привлекали к себе
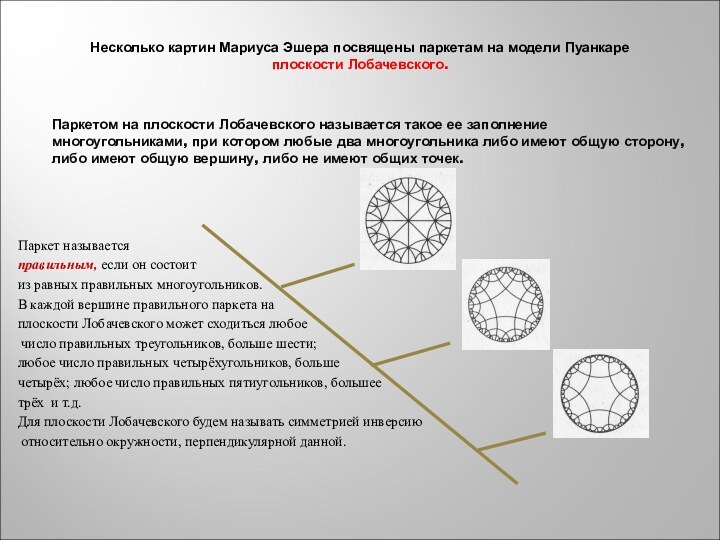
- 16. Несколько картин Мариуса Эшера посвящены паркетам на
- 17. Вывод: Строя шестиугольные ячейки пчелы наиболее
- 18. Скачать презентацию
- 19. Похожие презентации
Основополагающий вопрос Чему можно удивляться глядя на мир?














Слайд 3 Пчёлы – удивительные творения природы. Свои геометрические способности
они проявляют при построении сот.
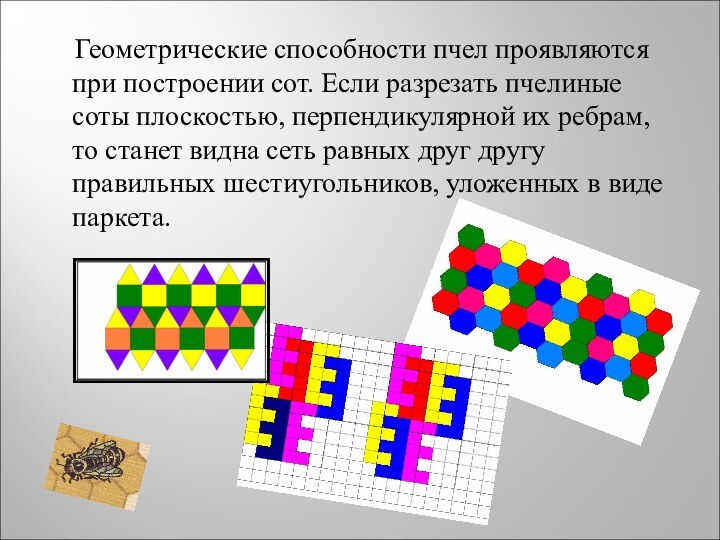
Слайд 4 Геометрические способности пчел проявляются при
построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их
ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета.Слайд 5 Выполняя несложные расчеты, убеждаемся, что такими многоугольниками могут
быть только правильные треугольники, квадраты или правильные шестиугольники.
Слайд 7
Почему пчелы выбрали именно шестиугольник?
Чтобы ответить на этот
вопрос, надо сравнить периметры разных многоугольников, имеющих одинаковую площадь.
Слайд 8 Для того чтобы выяснить, почему пчела строит соты,
перпендикулярное сечение которых есть правильный шестиугольник, а не правильный
треугольник или квадрат, рассматривается вспомогательная задачаСлайд 9 Даны три равновеликие друг другу фигуры
— правильный треугольник, квадрат и правильный шестиугольник. Какая из
данных фигур имеет наименьший периметр?Решение
Слайд 11 Действительно, сумма внутренних углов выпуклого n-угольника
равна (n-2)*180°, где n-число сторон многоугольника. Сумма углов, сходящихся
в одной вершине паркета, равна 360°.
Слайд 12
Тогда (n-2)*180°/n*k=360°. Отсюда k=2n/(n-2).
Если n=3, то k=6, т.е.
в одной вершине паркета могут сходиться 6 правильных треугольников.
Если
n=4,то k=4 т.е. в одной вершине паркета могут сходится 4 квадрата. Если n=5,то k=3.3т.е. не существует паркета из правильных пятиугольников.
Если n=6,то k=3т.е. в одной вершине паркета могут сходится 3 правильных шестиугольника.
Если n=7,то k=2.8т.е. не существует паркета из правильных семиугольников. Итак далее.
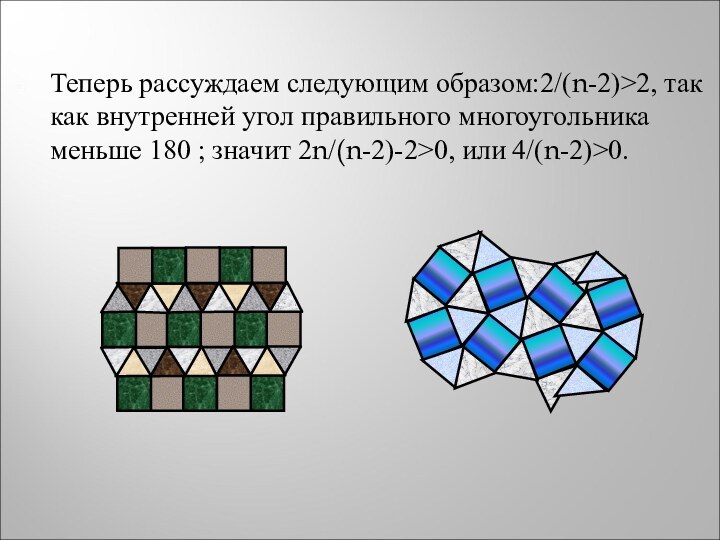
Слайд 13 Теперь рассуждаем следующим образом:2/(n-2)>2, так как внутренней угол
правильного многоугольника меньше 180 ; значит 2n/(n-2)-2>0, или 4/(n-2)>0.
Слайд 14 Как не согласиться с мнением
Пчелы из сказки «Тысяча и одна ночь»: «Мой дом
построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».Слайд 15 Паркеты с древних времён привлекали к себе внимание
людей. Ими мостили дороги, украшали полы в помещениях, стены
домов, использовали в декоративно-прикладном искусстве.Знаменитый голландский художник Мариус Эшер (1898 – 1972) посвятил паркетам несколько своих картин.
«небо и море»
«Ящерицы»
«Добро и зло»
Слайд 16 Несколько картин Мариуса Эшера посвящены паркетам на модели
Пуанкаре
плоскости Лобачевского.
Паркет называется
правильным, если он состоит
из
равных правильных многоугольников.В каждой вершине правильного паркета на
плоскости Лобачевского может сходиться любое
число правильных треугольников, больше шести;
любое число правильных четырёхугольников, больше
четырёх; любое число правильных пятиугольников, большее
трёх и т.д.
Для плоскости Лобачевского будем называть симметрией инверсию
относительно окружности, перпендикулярной данной.
Паркетом на плоскости Лобачевского называется такое ее заполнение многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.