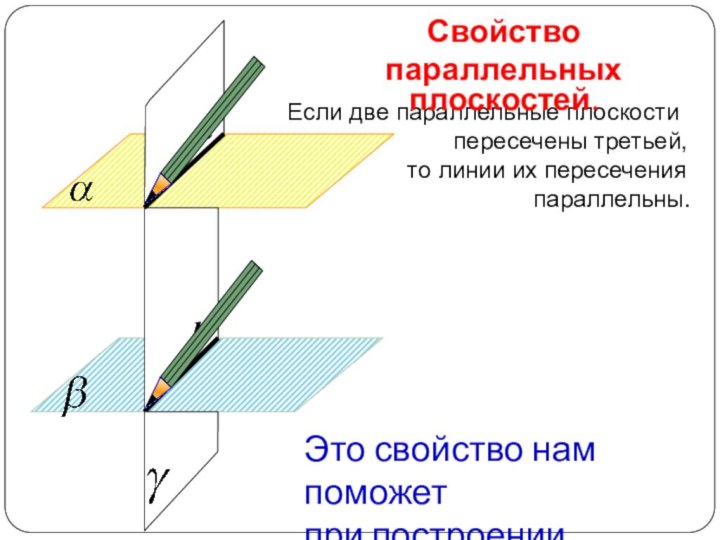
пересечены третьей,
то линии их пересечения
параллельны.
Свойство
параллельных плоскостей.
Это свойство нам поможет
при построении сечений.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











Свойство
параллельных плоскостей.
Это свойство нам поможет
при построении сечений.
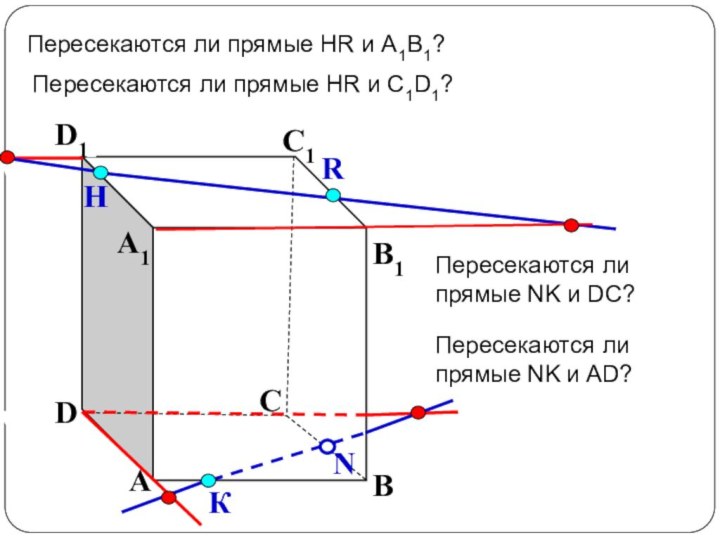
Пересекаются ли
прямые NK и АD?
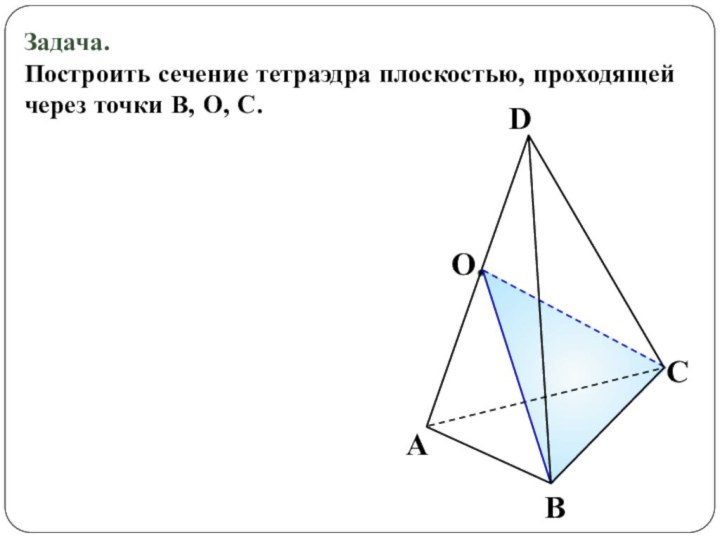
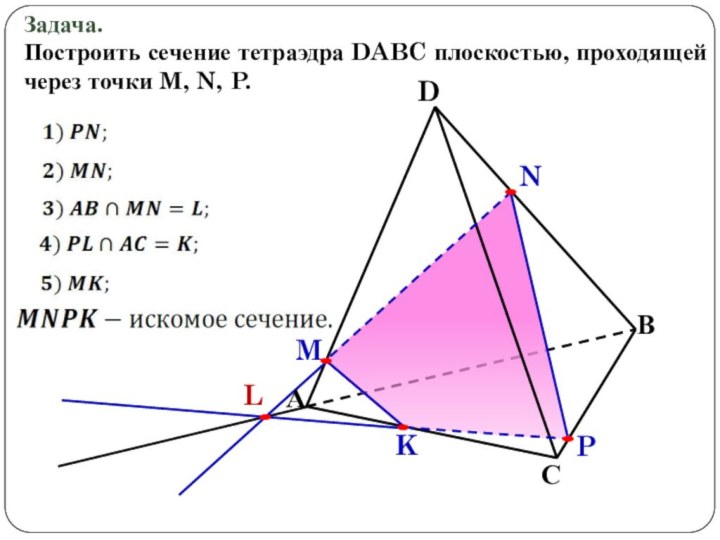
Построить сечение – значит определить, какие рёбра пересекает плоскость, вид полученного сечения и точное положение точек пересечения секущей плоскости с этими рёбрами.
Секущая плоскость пересекает грань ADC по прямой KL.
L
K
А
С
В
К
D
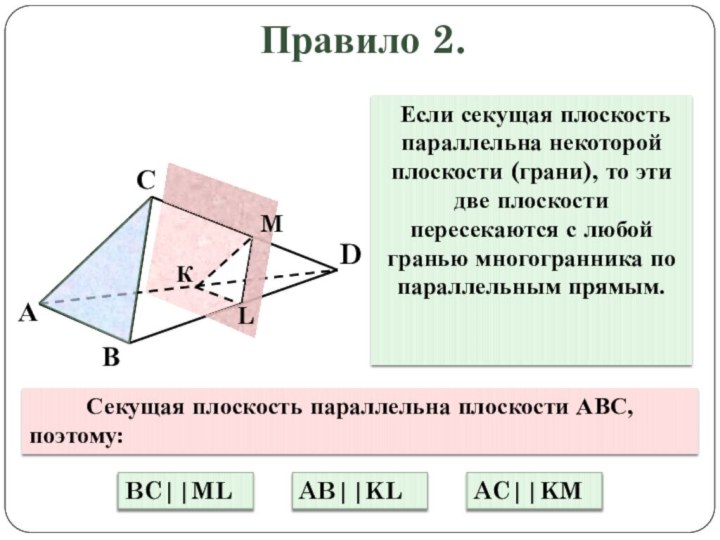
Секущая плоскость параллельна плоскости АВС,
поэтому:
BC||ML
AB||KL
AC||KM
L
M
С
D
А
В
М
D
А
С
В
М
К
L
N
К
L
N
М
Отметьте внутреннюю точку M грани АА1В1В.