Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Разрезание геометрических фигур на части

Содержание

2. ЗАДАЧИ НА РАЗРЕЗАНИЯТеорема Бойяи-Гервина гласит: любой многоугольник
3. ЗАДАНИЕ 1Разрежьте прямоугольник a ˟ 2a на такие части, чтобы из них можно было составить квадрат.
4. РЕШЕНИЕ ЗАДАНИЯ 1Прямоугольник ABCD разрежем на три
5. РЕШЕНИЕ ЗАДАНИЯ 1Треугольник АMD переместим так, чтобы
6. РЕШЕНИЕ ЗАДАНИЯ 1Треугольник АMD переместим так, чтобы
7. ЗАДАНИЕ 2РАЗРЕЗАТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК НА ЧАСТИ ТАК, ЧТОБЫ ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ КВАДРАТ
8. РЕШЕНИЕ ЗАДАНИЯ 2Обозначим данный правильный треугольник АВС.
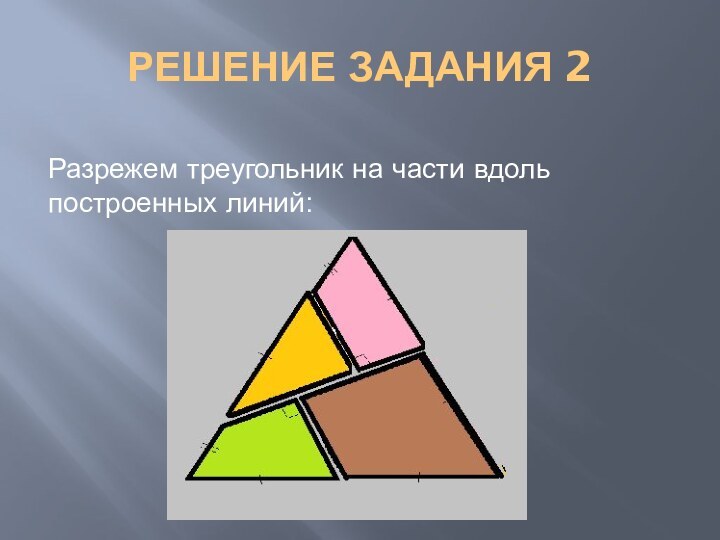
9. РЕШЕНИЕ ЗАДАНИЯ 2Разрежем треугольник на части вдоль построенных линий:
10. РЕШЕНИЕ ЗАДАНИЯ 2Четырехугольник КРЕС повернем по часовой
11. РЕШЕНИЕ ЗАДАНИЯ 2
12. РЕШЕНИЕ ЗАДАНИЯ 2
13. ЗАДАНИЕ 3РАЗРЕЗАТЬ КВАДРАТ НА ЧАСТИ ТАК, ЧТОБЫ ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ ДВА КВАДРАТА.
14. РЕШЕНИЕ ЗАДАНИЯ 3ОБОЗНАЧИМ ИСХОДНЫЙ КВАДРАТ ABCD. ОТМЕТИМ
15. РЕШЕНИЕ ЗАДАНИЯ 3PTEF – УЖЕ ГОТОВЫЙ КВАДРАТ. ИЗ ОСТАВШИХСЯ ЧЕТЫРЕХУГОЛЬНИКОВ СОСТАВИМ ВТОРОЙ КВАДРАТ.
16. РЕШЕНИЕ ЗАДАНИЯ 3ВЕРШИНЫ A, B, C И
17. ЗАДАНИЕ 4Из плотной бумаги вырезаны равносторонний треугольник
18. РЕШЕНИЕ ЗАДАНИЯ 4ТРЕУГОЛЬНИК РАЗРЕЖЕМ НА ЧАСТИ ТАК,
19. РЕШЕНИЕ ЗАДАНИЯ 4Теперь следует разделить на многоугольники
20. РЕШЕНИЕ ЗАДАНИЯ 4Возьмем квадрат со стороной 2а,
21. РЕШЕНИЕ ЗАДАНИЯ 4
22. РЕШЕНИЕ ЗАДАНИЯ 4Возьмем квадрат, составленный из частей
23. РЕШЕНИЕ ЗАДАНИЯ 4
24. ЗАДАНИЕ 5Крест составлен из пяти квадратов: один
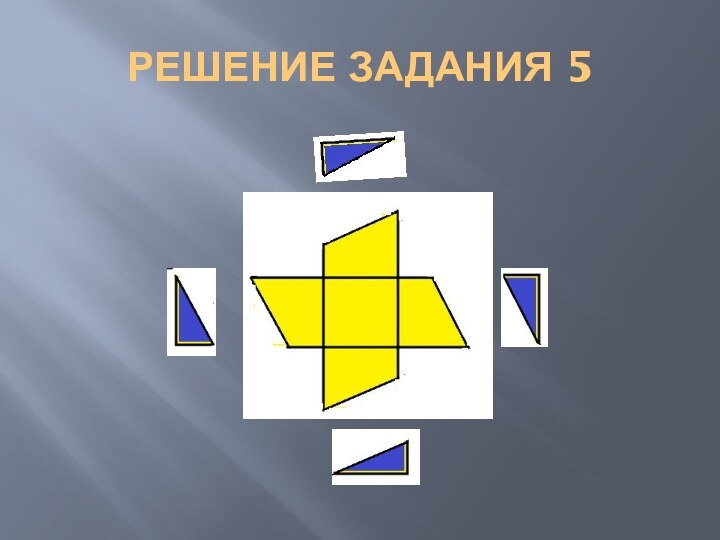
25. РЕШЕНИЕ ЗАДАНИЯ 5СОЕДИНИМ ВЕРШИНЫ КВАДРАТОВ ТАК, КАК ПОКАЗАНО НА РИСУНКЕ.
26. РЕШЕНИЕ ЗАДАНИЯ 5.ОТРЕЖЕМ ТРЕУГОЛЬНИКИ, ОКАЗАВШИЕСЯ ВНЕ КВАДРАТА. ПЕРЕМЕСТИМ ИХ ТАК, КАК ПОКАЗАНО НА СХЕМЕ.
27. РЕШЕНИЕ ЗАДАНИЯ 5
28. РЕШЕНИЕ ЗАДАНИЯ 5.
29. ЗАДАНИЕ 6Перекроить два произвольных квадрата в один.
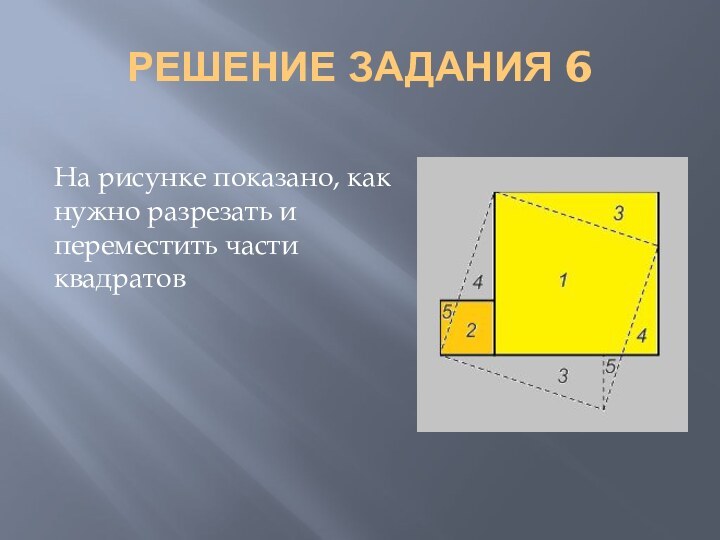
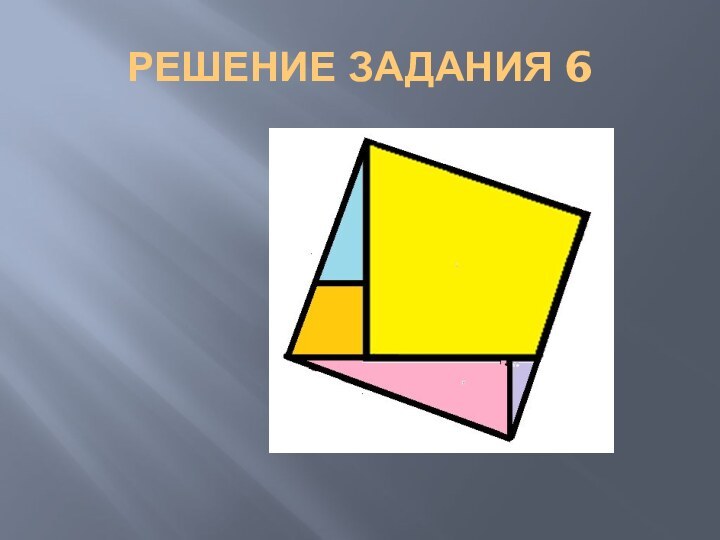
30. РЕШЕНИЕ ЗАДАНИЯ 6На рисунке показано, как нужно разрезать и переместить части квадратов
31. РЕШЕНИЕ ЗАДАНИЯ 6На рисунке показано, как нужно разрезать и переместить части квадратов
32. РЕШЕНИЕ ЗАДАНИЯ 6
33. РЕШЕНИЕ ЗАДАНИЯ 6
34. Скачать презентацию
35. Похожие презентации

ЗАДАЧИ НА РАЗРЕЗАНИЯТеорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат.

Главная
Геометрия
Разрезание геометрических фигур на части

Внеклассное занятие по математикеРАЗРЕЗАНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР НА ЧАСТИУчитель математики сош № 41 ОАО «РЖД» Кашенцева М.А.

ЗАДАЧИ НА РАЗРЕЗАНИЯТеорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части,

ЗАДАНИЕ 1Разрежьте прямоугольник a ˟ 2a на такие части, чтобы из них можно было составить квадрат.

РЕШЕНИЕ ЗАДАНИЯ 1Прямоугольник ABCD разрежем на три части по линиям MD и

РЕШЕНИЕ ЗАДАНИЯ 1Треугольник АMD переместим так, чтобы вершина М совместилась с вершиной

ЗАДАНИЕ 2РАЗРЕЗАТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК НА ЧАСТИ ТАК, ЧТОБЫ ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ КВАДРАТ

РЕШЕНИЕ ЗАДАНИЯ 2Обозначим данный правильный треугольник АВС. Необходимо разрезать ∆АВС на многоугольники

РЕШЕНИЕ ЗАДАНИЯ 2Разрежем треугольник на части вдоль построенных линий:

РЕШЕНИЕ ЗАДАНИЯ 2Четырехугольник КРЕС повернем по часовой стрелке относительно вершины К так,

ЗАДАНИЕ 3РАЗРЕЗАТЬ КВАДРАТ НА ЧАСТИ ТАК, ЧТОБЫ ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ ДВА КВАДРАТА.

РЕШЕНИЕ ЗАДАНИЯ 3ОБОЗНАЧИМ ИСХОДНЫЙ КВАДРАТ ABCD. ОТМЕТИМ СЕРЕДИНЫ СТОРОН КВАДРАТА – ТОЧКИ

РЕШЕНИЕ ЗАДАНИЯ 3PTEF – УЖЕ ГОТОВЫЙ КВАДРАТ. ИЗ ОСТАВШИХСЯ ЧЕТЫРЕХУГОЛЬНИКОВ СОСТАВИМ ВТОРОЙ КВАДРАТ.

РЕШЕНИЕ ЗАДАНИЯ 3ВЕРШИНЫ A, B, C И D СОВМЕСТИМ В ОДНУ ТОЧКУ,

ЗАДАНИЕ 4Из плотной бумаги вырезаны равносторонний треугольник и квадрат. Разрезать эти фигуры

РЕШЕНИЕ ЗАДАНИЯ 4ТРЕУГОЛЬНИК РАЗРЕЖЕМ НА ЧАСТИ ТАК, КАК ПОКАЗАНО В ЗАДАНИИ 2.

РЕШЕНИЕ ЗАДАНИЯ 4Теперь следует разделить на многоугольники квадрат так, чтобы из этих

РЕШЕНИЕ ЗАДАНИЯ 4Возьмем квадрат со стороной 2а, обозначим его LRSD.Проведем взаимно перпендикулярные

РЕШЕНИЕ ЗАДАНИЯ 4Возьмем квадрат, составленный из частей треугольника. Выложим четырехугольники – части

ЗАДАНИЕ 5Крест составлен из пяти квадратов: один квадрат в центре, а остальные

РЕШЕНИЕ ЗАДАНИЯ 5СОЕДИНИМ ВЕРШИНЫ КВАДРАТОВ ТАК, КАК ПОКАЗАНО НА РИСУНКЕ.

РЕШЕНИЕ ЗАДАНИЯ 5.ОТРЕЖЕМ ТРЕУГОЛЬНИКИ, ОКАЗАВШИЕСЯ ВНЕ КВАДРАТА. ПЕРЕМЕСТИМ ИХ ТАК, КАК ПОКАЗАНО НА СХЕМЕ.

ЗАДАНИЕ 6Перекроить два произвольных квадрата в один.

РЕШЕНИЕ ЗАДАНИЯ 6На рисунке показано, как нужно разрезать и переместить части квадратов

ЛИТЕРАТУРА1. А.В. Фарков «Внеклассная работа по математике» 5-11 классы, Москва, Айрис-пресс, 20092.

Слайды презентации

Слайд 2 ЗАДАЧИ НА РАЗРЕЗАНИЯ
Теорема Бойяи-Гервина гласит: любой многоугольник можно

ЗАДАЧИ НА РАЗРЕЗАНИЯТеорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на

так разрезать на части, что из этих частей удастся

сложить квадрат.

Слайд 3 ЗАДАНИЕ 1
Разрежьте прямоугольник a ˟ 2a на такие

части, чтобы из них можно было составить квадрат.

Слайд 4 РЕШЕНИЕ ЗАДАНИЯ 1
Прямоугольник ABCD разрежем на три части

РЕШЕНИЕ ЗАДАНИЯ 1Прямоугольник ABCD разрежем на три части по линиям MD

по линиям MD и MC
(М – середина АВ)

Слайд 5 РЕШЕНИЕ ЗАДАНИЯ 1
Треугольник АMD переместим так, чтобы вершина

РЕШЕНИЕ ЗАДАНИЯ 1Треугольник АMD переместим так, чтобы вершина М совместилась с

М совместилась с вершиной С, катет АМ переместится на

отрезок DС.
Треугольник МВС переместим влево и вниз так, что катет МВ наложится на половину отрезка DС

Слайд 6 РЕШЕНИЕ ЗАДАНИЯ 1
Треугольник АMD переместим так, чтобы вершина

М совместилась с вершиной С, катет АМ переместится на

отрезок DС.
Треугольник МВС переместим влево и вниз так, что катет МВ наложится на половину отрезка DС

Слайд 7 ЗАДАНИЕ 2
РАЗРЕЗАТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК НА ЧАСТИ ТАК, ЧТОБЫ

ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ КВАДРАТ

Слайд 8 РЕШЕНИЕ ЗАДАНИЯ 2
Обозначим данный правильный треугольник АВС. Необходимо

РЕШЕНИЕ ЗАДАНИЯ 2Обозначим данный правильный треугольник АВС. Необходимо разрезать ∆АВС на

разрезать ∆АВС на многоугольники так, чтобы из них можно

было сложить квадрат. Тогда эти многоугольники должны иметь по крайней мере по одному прямому углу.
Пусть К – середина СВ, Т – середина АВ, точки М и Е выберем на стороне АС так, что МЕ=АТ=ТВ=ВК=СК=а, АМ=ЕС=а/2.
Проведем отрезок МК и перпендикулярные к нему отрезки ЕР и ТН.

Слайд 9 РЕШЕНИЕ ЗАДАНИЯ 2
Разрежем треугольник на части вдоль построенных

линий:

Слайд 10 РЕШЕНИЕ ЗАДАНИЯ 2
Четырехугольник КРЕС повернем по часовой стрелке

РЕШЕНИЕ ЗАДАНИЯ 2Четырехугольник КРЕС повернем по часовой стрелке относительно вершины К

относительно вершины К так, что СК совместится с отрезком

КВ.
Четырехугольник АМНТ повернем по часовой стрелке относительно вершины Т так, что АТ совместится с ТВ.
Треугольник МЕР переместим так, что в результате получится квадрат:

Слайд 11 РЕШЕНИЕ ЗАДАНИЯ 2

Слайд 12 РЕШЕНИЕ ЗАДАНИЯ 2

Слайд 13 ЗАДАНИЕ 3
РАЗРЕЗАТЬ КВАДРАТ НА ЧАСТИ ТАК, ЧТОБЫ ИЗ

НИХ МОЖНО БЫЛО СЛОЖИТЬ ДВА КВАДРАТА.

Слайд 14 РЕШЕНИЕ ЗАДАНИЯ 3
ОБОЗНАЧИМ ИСХОДНЫЙ КВАДРАТ ABCD. ОТМЕТИМ СЕРЕДИНЫ

РЕШЕНИЕ ЗАДАНИЯ 3ОБОЗНАЧИМ ИСХОДНЫЙ КВАДРАТ ABCD. ОТМЕТИМ СЕРЕДИНЫ СТОРОН КВАДРАТА –

СТОРОН КВАДРАТА – ТОЧКИ M, N, K, H. ПРОВЕДЕМ

ОТРЕЗКИ МТ, НЕ, КF И NР – ЧАСТИ ОТРЕЗКОВ МС, НВ, КА И ND СООТВЕТСТВЕННО.

РАЗРЕЗАВ КВАДРАТ ABCD ПО ПРОВЕДЕННЫМ ЛИНИЯМ, ПОЛУЧИМ КВАДРАТ PTEF И ЧЕТЫРЕ ЧЕТЫРЕХУГОЛЬНИКА MDHT, HCKE, KBNF И NAMP.