Презентация на тему по математике Решение геометрических задач при подготовке к ОГЭ

воду, а если хотите
научиться решать задачи, то решайте их.
Методы

решения геометрических задач.

геометрический – когда требуемое утверждение
выводится с помощью логических рассуждений из ряда известных теорем; 

алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; 

комбинированный – когда на одних этапах решение ведется геометрическим
методом, а на других – алгебраическим.

Справочные

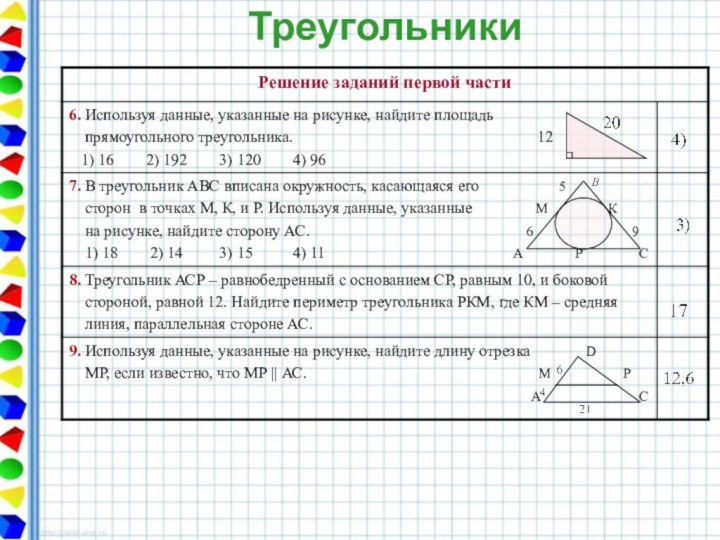
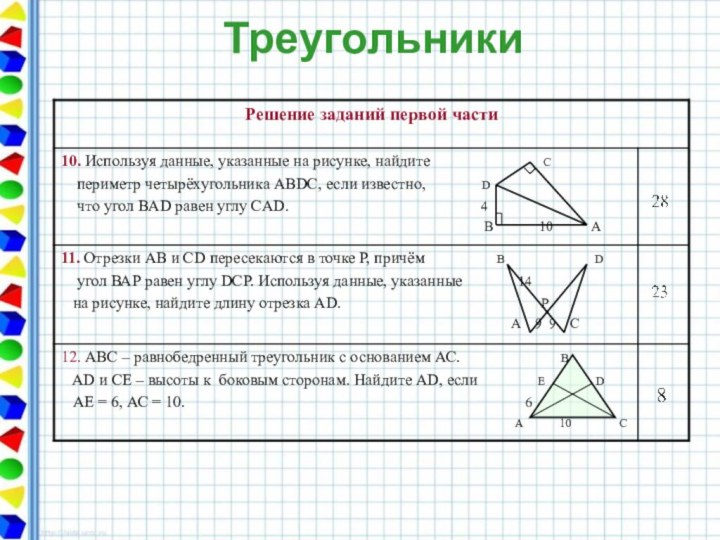
сведения Треугольники

стороны многоугольника, два радиуса или равные диагонали:

d
a R r r
R R R d
a

Примеры прямоугольных треугольников
(вписанный угол опирается на диаметр)

Справочные сведения Правильные многоугольники

правило, помимо свойств, относящих-
ся к равнобедренному треугольнику, используют

свойства прямоугольного треугольника, т. к.
медиана, проведённая к основанию, делит равнобедренный треугольник на два прямоугольных.

1. Найдите основание равнобедренного треугольника, если оно в 3 раза меньше
боковой стороны, а медиана, проведённая к боковой стороне, равна .

Решение: 1 способ
1) Обозначим АС = х, тогда ВС = 3х, МС = 1,5х.

2) : по теореме косинусов

3) Пусть ВН – высота к основанию АС.

4) Получаем:



- 6 не удовл. смыслу задачи
Отсюда АС = 6.
Ответ: 6.

Треугольники Решение заданий второй части

3 раза меньше боковой
стороны, а медиана, проведённая

к боковой стороне, равна .
2 способ: используется приём, позволяющий быстро решать задачи, где речь идёт о медиане.
Медиана АМ продлевается за точку М и на её продолжении откладывается отрезок МD, равный
медиане.
Рассматривается параллелограмм АВDС и используется формула, связывающая его
стороны и диагонали.
Решение:
1) Пусть АС – основание треугольника, АМ – медиана.
Отложим на луче АМ отрезок МD = АМ
Тогда АСВD – параллелограмм, т. к.его диагонали пересекаются
в середине.
2) Обозначим АС = х, АВ = ВС = 3х, тогда по свойству сторон и
диагоналей параллелограмма имеем: ,
или


Ответ: 6.

Треугольники Решение заданий второй части

13 вписан равнобедренный треугольник. Известно, что синус
угла при

основании треугольника равен . Радиус ОМ пересекает под прямым углом
боковую сторону в точке К. Найдите длину отрезка ОК.
Решение:
1) Угол при основании равнобедренного треугольника может быть только
острым, значит, центр О с вершиной А лежит по одну сторону от хорды ВС.
Тогда - центральный, соответствующий углу А. Отсюда



2) Δ ВОС – равнобедренный, ОК – высота, проведённая к основанию, тогда ОК – биссектриса угла О, отсюда имеем:

3)

Ответ: 5.

13 вписан равнобедренный треугольник. Известно, что синус
угла при

основании треугольника равен . Радиус ОМ пересекает под прямым углом
боковую сторону в точке К. Найдите длину отрезка ОК.


Решение:

1)

2)


3) Достроим радиус ОМ до диаметра РМ, тогда РМ =26.
Пусть МК = х. По свойству отрезков хорд получим



Ответ:5.

применяют в задачах, связанных с вычислением
элементов равнобедренных или

прямоугольных треугольников. При решении задач бывает
полезно отметить на рисунке точки касания и отметить равные отрезки одинаковыми буквами
или чёрточками, используя при этом свойства рассматриваемого треугольника.
Окружность с центром О, вписана в равнобедренный треугольник АВС с основанием АС.
Она касается стороны ВС в точке М, причём отрезок ВМ составляет 0,4 боковой стороны.
Найдите высоту, проведённую к боковой стороне, если АС = 30.
Решение:
1) Обозначим буквой Н точку касания вписанной окружности с основанием.
Так как ΔАВС – равнобедренный, то центр О лежит на высоте к основанию,
т. е. ВН – высота и Н – середина основания.
2) Если считать ВМ = 2х и СМ = 3х, то АВ = ВС = 5х.
По свойству отрезков касательных имеем СН = 3х, 3х = 15, АВ = 25.
3) По теореме Пифагора


4) SАВС =0,5 ВН· АС = 0,5 АВ · h, отсюда h = (20 · 30) : 25 = 24.
Ответ: 24.

иногда используется отношение площадей
треугольников. Отношение площадей подобных треугольников равно

квадрату
отношения сходственных сторон (или квадрату коэффициента подобия).

Из формулы площади треугольника можно вывести ещё два следствия:
- если треугольники имеют общее основание (или равные основания), то их
площади относятся, как высоты, проведённые к этим основаниям;
- если треугольники имеют общую высоту (или равные высоты), то их площади
относятся, как основания.

21. Известно, что сторона МР = 7, медиана
РА

= , а в треугольнике АРМ сторона АМ – наименьшая. Найдите сторону МК.

Решение:
1)

2)

Т. к. МА – наименьшая сторона в треугольнике АРМ, то α не
может быть тупым, α = .
3) В треугольнике МАР по теореме косинусов:




Ответ: 10.

прямым углом С биссектриса ВК делит катет АС на

отрезки АК = 15 и КС = 12. Найдите площадь треугольника АВК.

Решение:
1) По свойству биссектрисы треугольника
Тогда АВ = 5х, ВС = 4х,




2) (т. к. эти треугольники имеют одну
и ту же высоту ВС).
Значит,

Ответ: 270.

фанеры вырезали равносторонний треугольник со сторонами 10 дм, 10

дм и
12 дм. Сколько килограммов краски потребуется, чтобы его покрасить, если на
поверхности расходуется 0,015 кг краски?

Решение:

По формуле Герона получаем:




Расход краски равен 48 · 0,015 = 0,72 (кг)

Ответ: 0, 72.

использовать способ основанный на равенстве угла падения и
угла

отражения света. Для этого на некотором расстоянии от измеряемого дерева, на ровной земле, в
точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой
наблюдатель видит в зеркале верхушку А дерева.



А















В С D

поступать, если к измеряемому объекту невозможно подойти вплотную?
А) Задача

решается двукратным применением описанного выше способа – помещение зеркала
высота равна возвышению глаза наблюдателя, умноженному на отношение расстояния между
положениями зеркала к разности расстояний наблюдателя от зеркала.

Б) На прямой, проходящей через основание Н предмета, отмечают точки В и С на определён-
ном расстоянии а друг от друга и измеряют углы АВН и АСВ:
По теореме синусов:






Способ рассматривается в учебнике п.100,
«Измерительные работы».
Задача № 1036, 1038.

м одна от другой стоят две сосны. Высота одной

31 м, другой, молодой – всего 6 м. Можете ли вы определить как велико расстояние между их макушками?

Решение:

По теореме Пифагора расстояние АВ между
верхушками сосен равно







Ответ: 47 м.

ВС от отвесного шеста АВ высотою 4,2 м имеет

6,5 длины. Какова в этот
момент высота Солнца над горизонтом, т. е. как велик угол С?

Решение:









Ответ:

изображён –
ного на рисунке, если рост человека 1,7м, а

в резуль-
тате измерений получено: ВС = 9м, CD = 1,5м.


Решение: В С D
A

E
1.7
B 9 C 1.5 D




Ответ: 10,2 м.

воткнуть в землю под прямым углом шест

М
выше роста наблюдателя на расстоянии от дома. Затем следует
отойти от шеста назад по продолжению до той точки О, с которой
можно увидеть высшую точку М на одной линии с верхней О N
точкой шеста. Далее, стоя на том же месте, необходимо P
отметить на шесте и на доме 2 точки и N, лежащие на горизонтальной прямой.
Определите высоту МР дома, если рост человека

Решение:
1)

подобен по первому признаку
Отсюда следует пропорциональность сторон:

MP = MN + NP = 6 + 1,7 = 7,7 (м).
Ответ: 7,7 м.

высоту CD = h холма, необходимо с помощью угломерных
инструментов

измерить угол α, под которым видна вершина С холма из точки А, затем
отойти на расстояние АВ = d, находясь в плоскости ACD, и измерить угол β, под которым
видна вершина С. - рост наблюдателя. Найдите высоту холма, если
.

С Решение:

1)
β α как стороны прямоугольников
2)
3)


4) В прямоугольном
5)

Ответ: 88,3м.

работы для проверки состояния более
сложных предметных умений –

анализировать ситуацию, разрабатывать способ
решения, проводить математически грамотные рассуждения.

Характеризуя высокий уровень подготовки по предмету, как правило, выделяют
следующие его качества:
умение выполнять чертёж, соответствующий ситуации, представленной в условии задачи;
прочное владение системой знаний, указанных в школьной программе;
умение обосновывать сделанные выводы ссылкой на теоремы и определения;
умение строить логически верную цепочку доказательных рассуждений, шагов
решения , которые помогают прийти к требуемому выводу;
умение синтезировать информацию из различных разделов курса геометрии для решения поставленной проблемы;
умение математически грамотно записать решение задачи.