мудрецов
он и геометрии у греков первый открыватель,
и
природы точнейший испытатель, и светил опытнейший наблюдатель
«Познать себя трудно, советовать другим легко»
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть














«Познать себя трудно, советовать другим легко»
Биография Фалеса Милетского
Достоверно известно только то, что Фалес был знатного рода, и получил на родине хорошее образование. Собственно милетское происхождение Фалеса ставится под сомнение; сообщают, что его род имел финикийские корни, и что в Милете он был пришельцем.
Некоторые источники утверждают, что Фалес жил в одиночестве и сторонился государственных дел; другие — что был женат, имел сына Кибиста; третьи — что оставаясь холостяком, усыновил сына сестры.
Да, оказывается, все достаточно просто. Вот что придумал Фалес Милетский. Он подождал пока длина его тени и его рост совпадут, а затем с помощью теоремы о подобии треугольников нашел длину тени пирамиды, которая соответственно, была равна тени, отбрасываемой пирамидой.
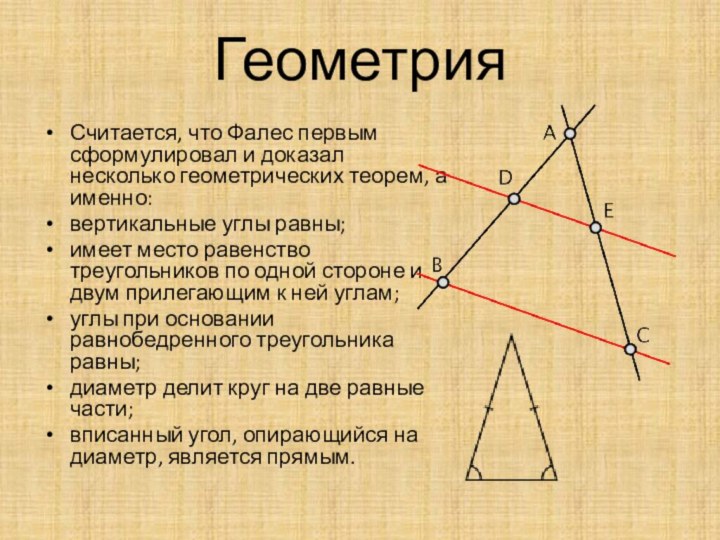
углы при основании равнобедренного треугольника равны;
диаметр делит круг пополам;
Фалес первый вписал прямоугольный треугольник в круг
и в благодарность богам принёс в жертву быка
Считается, что Фалес первый разбил небесную сферу на пять зон: арктический всегда видимый пояс, летний тропик, небесный экватор, зимний тропик, антарктический невидимый пояс.
Считается, что Фалес “изобрел глобус”. Можно утверждать, что Фалес (начав с геометрического изучения углов) создал “математический метод” в изучении движения небесных тел.
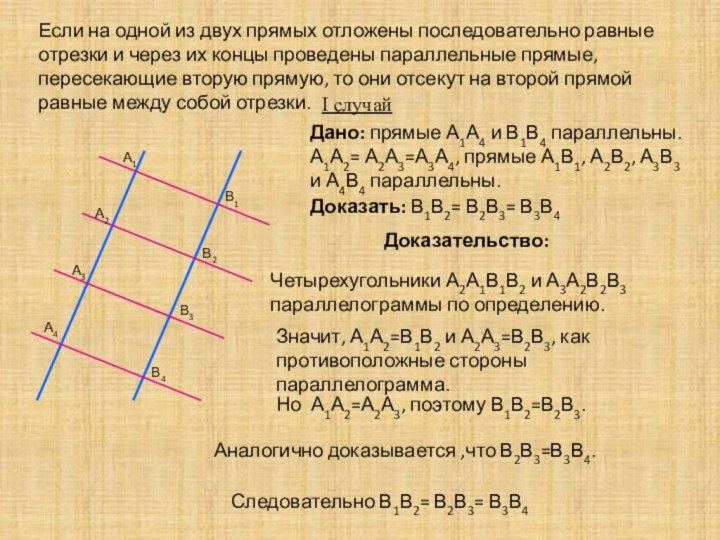
I случай
А1
А2
А3
А4
В1
В2
В3
В4
Дано: прямые А1А4 и В1В4 параллельны. А1А2= А2А3=А3А4, прямые А1В1, А2В2, А3В3 и А4В4 параллельны.
Доказать: В1В2= В2В3= В3В4
Доказательство:
Четырехугольники А2А1В1В2 и А3А2В2В3 параллелограммы по определению.
Значит, А1А2=В1В2 и А2А3=В2В3, как противоположные стороны параллелограмма.
Но А1А2=А2А3, поэтому В1В2=В2В3.
Аналогично доказывается ,что В2В3=В3В4.
Следовательно В1В2= В2В3= В3В4
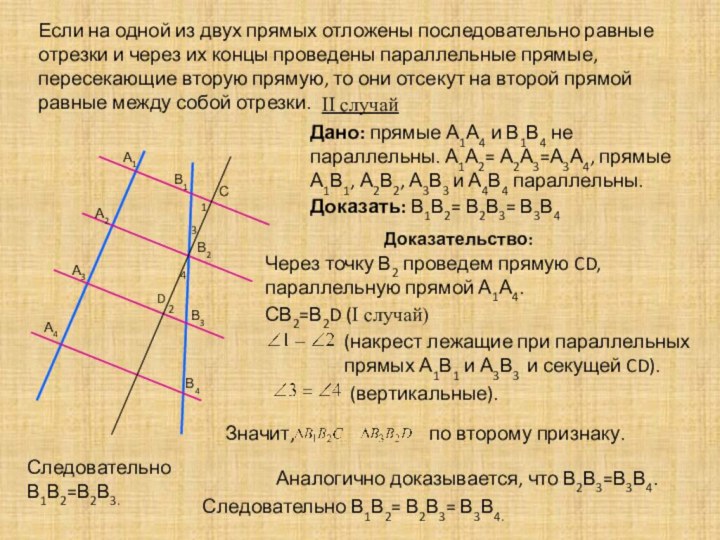
II случай
А1
А2
А3
А4
В1
В2
В3
В4
Дано: прямые А1А4 и В1В4 не параллельны. А1А2= А2А3=А3А4, прямые А1В1, А2В2, А3В3 и А4В4 параллельны.
Доказать: В1В2= В2В3= В3В4
Доказательство:
С
D
1
3
2
4
Через точку В2 проведем прямую CD, параллельную прямой А1А4.
СВ2=В2D (I случай)
(накрест лежащие при параллельных прямых А1В1 и А3В3 и секущей CD).
(вертикальные).
Значит,
по второму признаку.
Следовательно В1В2=В2В3.
Аналогично доказывается, что В2В3=В3В4.
Следовательно В1В2= В2В3= В3В4.
Геометрия
Смерть