Презентация на тему по математике. Творческая работа Живая геометрия - геометрия природы

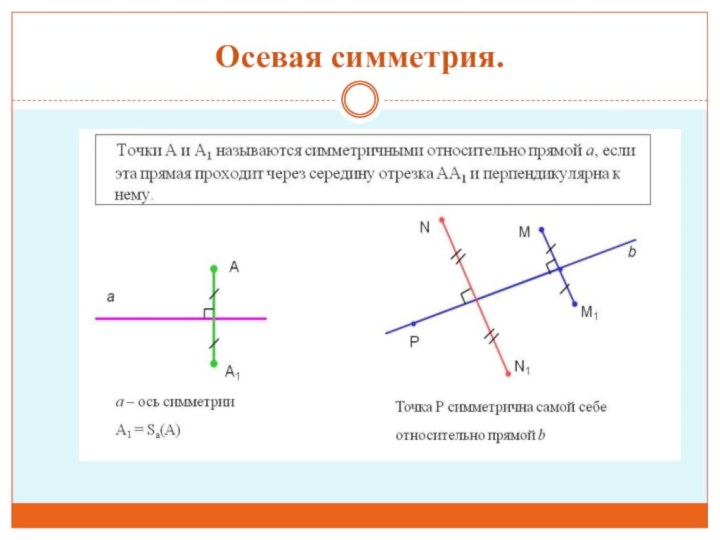
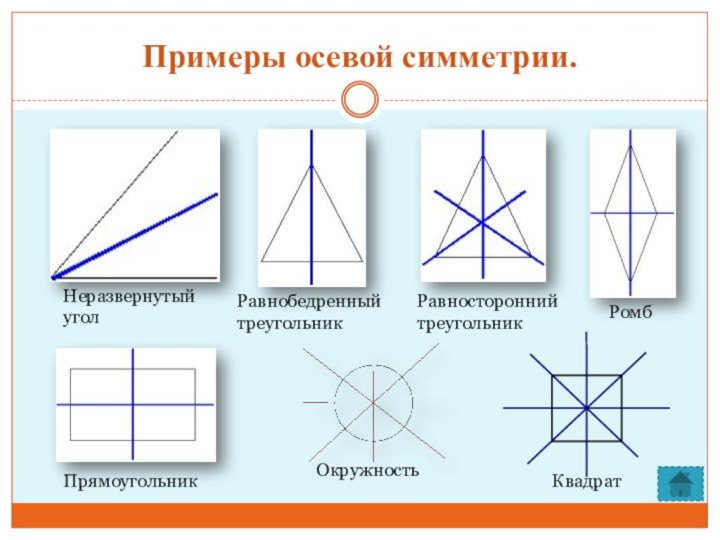
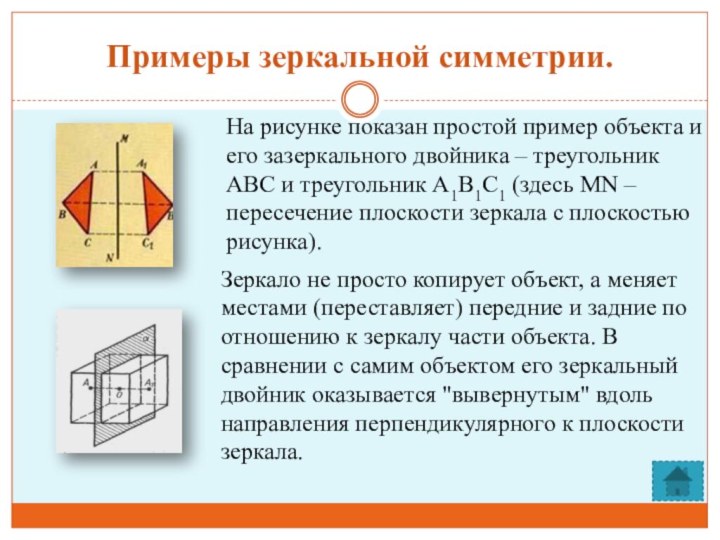
А.Д.Александров

При изучении природы мы находим в ней все больше эстетических признаков, которые выявляются, как правило, не сразу, но после детального математического анализа. В 5 веке до н. э. на явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы, в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году, как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика. 

человека, находя своё проявление как в живой, так и

в неживой природе. Объяснение законов симметрии важно для понимания красоты, гармонии, жизни.
Предмет данного исследования: симметрия как одна из математических основ за­конов красоты, взаимосвязи науки математики с окружающими нас живыми объектами.
Цель: изучить научно-популярную литературу и исследовать проявление симметрии в растительном и животном мире.
Задачи: 1. Узнать о том, что такое симметрия и на что она распространяется. 2. Убедиться на собственном опыте, что природа может иметь связь с геометрией.
Гипотеза: Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нём, открывать новое, понимать красоту и мудрость окружающего мира поможет этот проект.
Предполагаемое практическое применение: возможность применения полученных знаний: при решении предметных задач, в повседневной жизни, при изучении тем на других предметах; использование результатов исследования в виде презентаций, наглядного материала, буклета учителями – предметниками, в качестве вспомогательного материала при проведении интегрированных уроков по различным учебным дисциплинам.

Центральная симметрия.

Поворотная симметрия.

Фрактальная симметрия.

Примеры симметрии в природе.

Квадрат

наблюдения. Как показывает само название, зеркальная симметрия связывает некоторый

предмет и его изображение в плоском зеркале. 

и его зазеркального двойника – треугольник ABC и треугольник

А1В1С1 (здесь MN – пересечение плоскости зеркала с плоскостью рисунка).

Зеркало не просто копирует объект, а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта. В сравнении с самим объектом его зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала.

окружность и параллелограмм.

при повороте вокруг некоторой оси на угол, равный 360/n

(или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.

второму, если он, перемещаясь любым разрешённым способом в пространстве

и во времени (то есть, эволюционируя), может стать структурно идентичным второму объекту, условно неподвижному в пространстве и времени.

характерным свойством: цветок можно повернуть так, что каждый лепесток

займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии.

многоуровневого подобия самому себе.
Многие объекты в природе обладают фрактальными

свойствами:
побережья морей и берега рек

природе можно наблюдать геометрию в виде симметрий и фракталов.

Я выяснила, что симметрия принадлежит к числу широко и повсеместно распространенных явлений. Симметрия проникла в животный и растительный мир, стала там полновластной хозяйкой. Ее всеобщность служит эффективным инструментом познания природы. Природа преподносит нам все много новых подарков. Наука все больше и больше узнаёт о природе, о её строении и о том, как тесно с ней связаны такие науки, как геометрия и математика. Это удивительно!