Слайд 2
Платон
С древнейших времен велик интерес человека к правильным
многогранникам.
Платон (427–347 до н.э.) – первым описал их
свойства.
Именно поэтому правильные многогранники называют телами Платона.
Слайд 3
Четыре сущности природы были известны человечеству: огонь, вода,
земля и воздух.
По мнению Платона, их атомы имели
вид правильных многогранников
Слайд 4
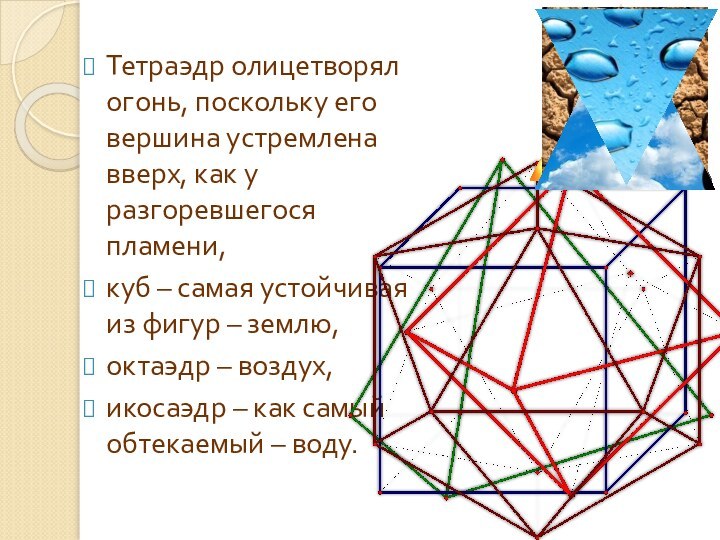
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх,
как у разгоревшегося пламени,
куб – самая устойчивая из фигур
– землю,
октаэдр – воздух,
икосаэдр – как самый обтекаемый – воду.
Слайд 5
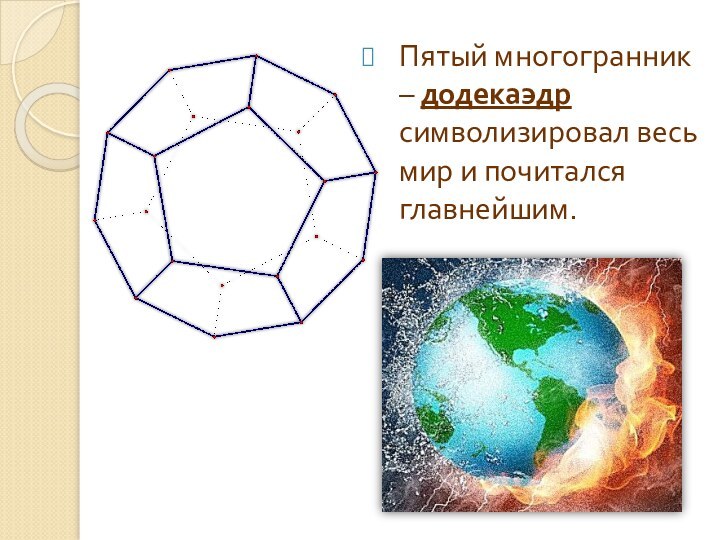
Пятый многогранник – додекаэдр символизировал весь мир и
почитался главнейшим.
Слайд 6
Кеплер
Иоганн Кеплер (1571-630гг.) – немецкий астроном. открыл
законы движения планет.
В 1596 году Кеплер предложил правило,
по которому вокруг сферы Земли описывается додекаэдр, а в нее вписывается икосаэдр. («Гармония мира», 1619г.)
Геометрическая модель Солнечной системы,
основанная на «платоновых телах».
Слайд 7
Икосаэдро-додекаэдровая
структура Земли
Советские инженеры В.Макаров и В.Морозов утверждают,
что в настоящее время процессы жизнедеятельности Земли имеют структуру
додекаэдра-икосаэдра.
На стыках додекаэдров и икосаэдров находятся основные залежи полезных ископаемых, загадочные явления, центры древних и современных цивилизаций.
Слайд 8
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
5 ПЛАТОНОВЫХ ТЕЛ
Выпуклый многогранник называется правильным,
если все его грани – равные правильные многоугольники и
в каждой его вершине сходится одно и то же число ребер.
Также все ребра правильного многоугольника равны, как и все двугранные углы, содержащие две грани с общим ребром.
Правильного многогранника, гранями которого являются n-угольники при n > или =6, не существует!
Слайд 9
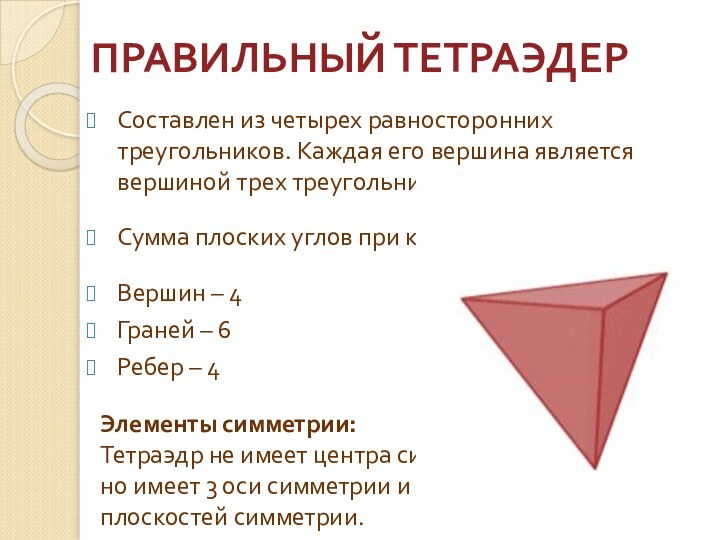
ПРАВИЛЬНЫЙ ТЕТРАЭДЕР
Элементы симметрии:
Тетраэдр не имеет центра симметрии, но
имеет 3 оси симметрии и 6 плоскостей симметрии.
Составлен из
четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников.
Сумма плоских углов при каждой вершине ровна 180°.
Вершин – 4
Граней – 6
Ребер – 4
Слайд 10
ПРАВИЛЬНЫЙ ГЕКСАЭДР (КУБ)
Составлен из шести квадратов. Каждая вершина
куба является вершиной трех квадратов.
Сумма плоских углов при каждой
вершине ровна 270°.
6 граней
8 вершин
12 ребер
Элементы симметрии:
Куб имеет центр симметрии - центр куба, 9 осей и плоскостей симметрии.
Слайд 11
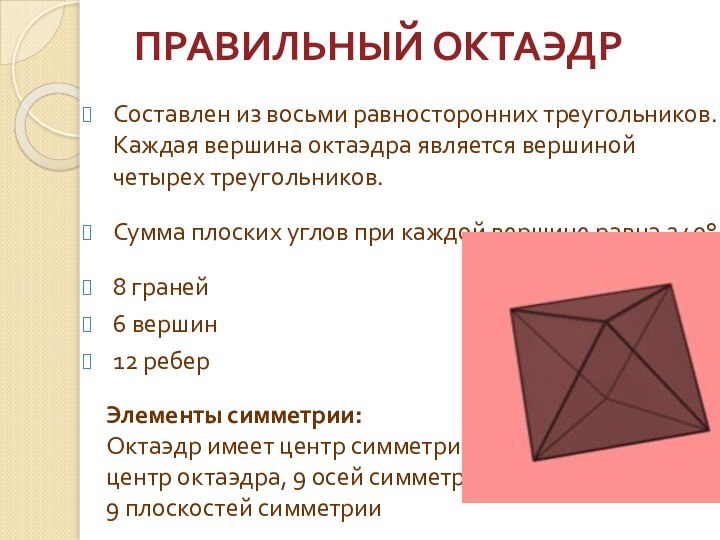
ПРАВИЛЬНЫЙ ОКТАЭДР
Составлен из восьми равносторонних треугольников. Каждая вершина
октаэдра является вершиной четырех треугольников.
Сумма плоских углов при каждой
вершине равна 240°.
8 граней
6 вершин
12 ребер
Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии
Слайд 12
ПРАВИЛЬНЫЙ ИКОСАЭДР
Составлен из двадцати равносторонних треугольников. Каждая вершина
икосаэдра является вершиной пяти треугольников
Сумма плоских углов при каждой
вершине равна 300°
20 граней,
12 вершин
30 ребер
Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии
Слайд 13
ПРАВИЛЬНЫЙ ДОДЕКАЭДР
Составлен из двенадцати правильных пятиугольников. Каждая вершина
додекаэдра является вершиной трех правильных пятиугольников
Сумма плоских углов при
каждой вершине ровна 324°
12 граней
20 вершин
30 ребер
Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Слайд 14
Эйлер
Следующий серьезный шаг в науке о многогранниках
был сделан в XVIII веке Леонардом Эйлером
(1707-1783), который вывел формулу о соотношении между числом вершин, ребер и граней выпуклого многогранника.
Она окончательно навела математический порядок в многообразном мире многогранников.
Слайд 15
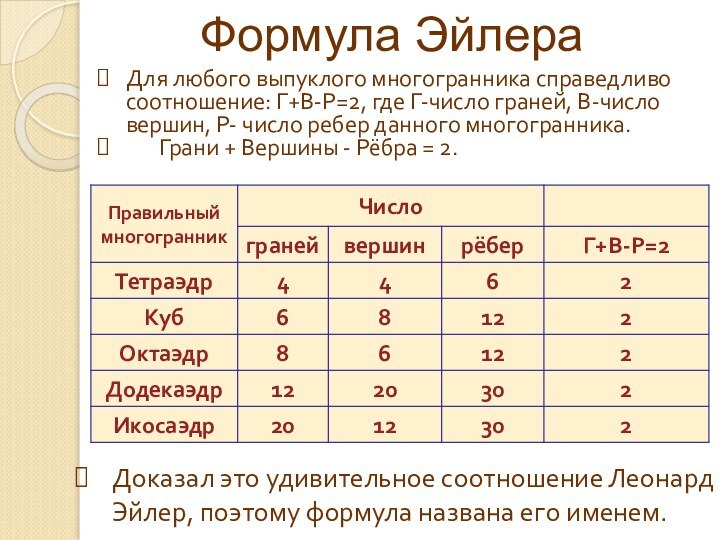
Формула Эйлера
Для любого выпуклого многогранника справедливо соотношение: Г+В-Р=2,
где Г-число граней, В-число вершин, Р- число ребер данного
многогранника.
Грани + Вершины - Рёбра = 2.
Доказал это удивительное соотношение Леонард Эйлер, поэтому формула названа его именем.
Слайд 16
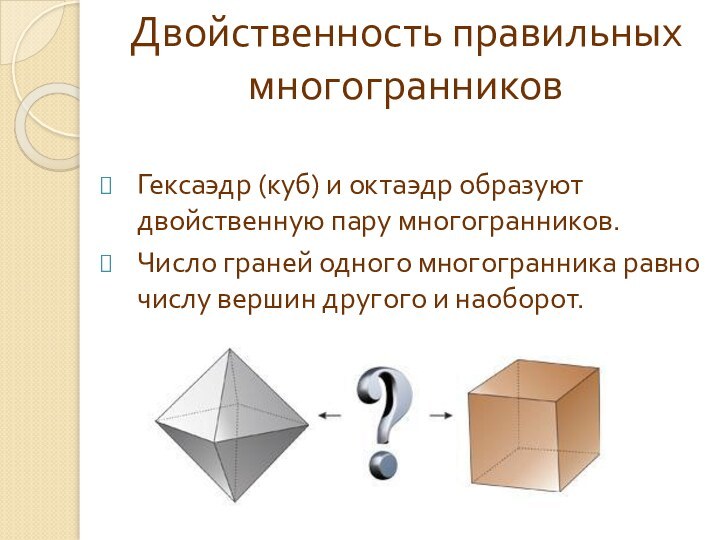
Двойственность правильных многогранников
Гексаэдр (куб) и октаэдр образуют двойственную
пару многогранников.
Число граней одного многогранника равно числу вершин
другого и наоборот.
Слайд 17
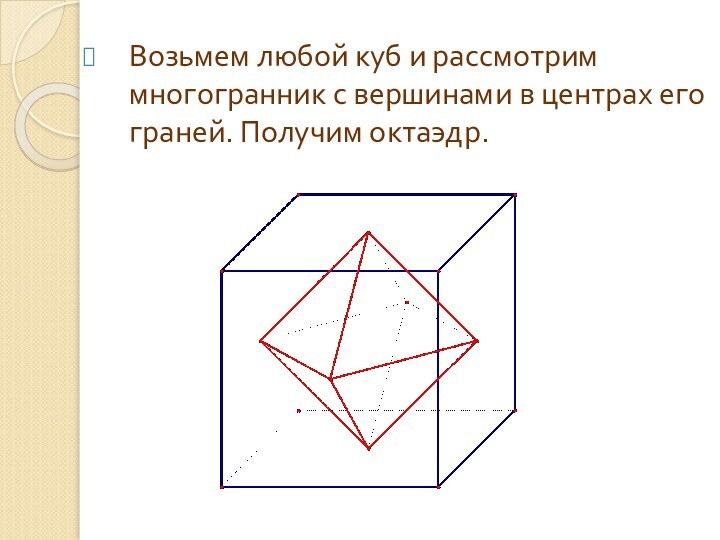
Возьмем любой куб и рассмотрим многогранник с вершинами
в центрах его граней. Получим октаэдр.
Слайд 18
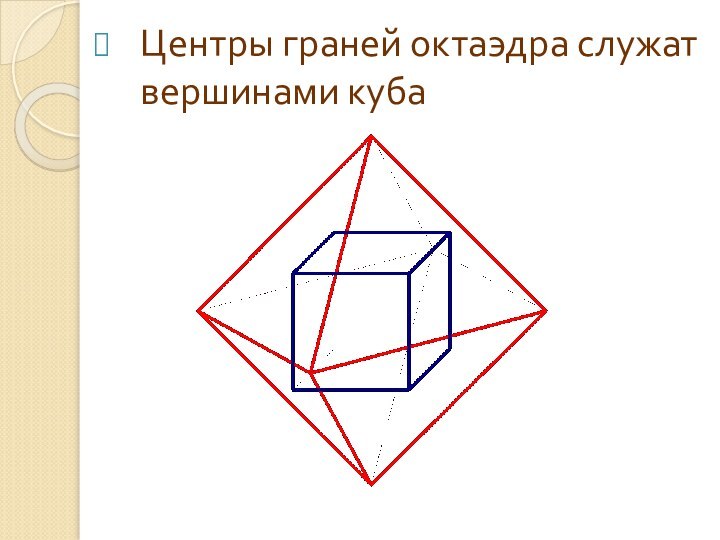
Центры граней октаэдра служат вершинами куба
Слайд 19
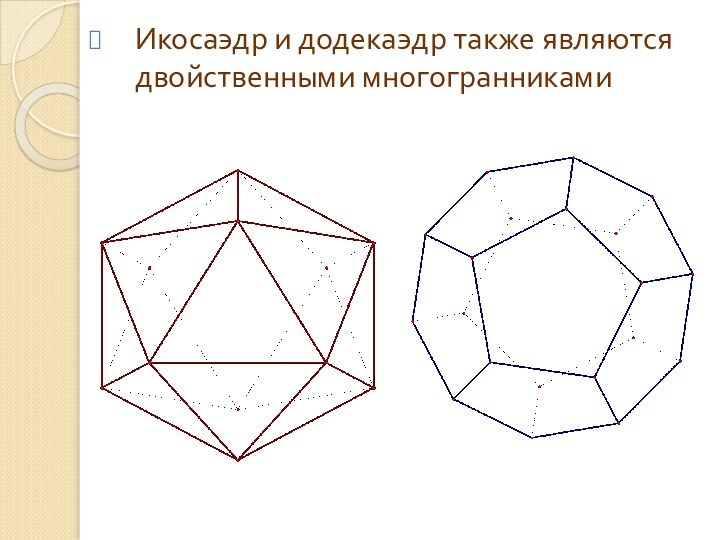
Икосаэдр и додекаэдр также являются двойственными многогранниками
Слайд 20
Додекаэдр и икосаэдр
В додекаэдр можно вписать икосаэдр.
Вершинами
икосаэдра являются центры граней додекаэдра. В свою очередь, центры
граней икосаэдра образуют вершины вписанного в него додекаэдра.
Слайд 21
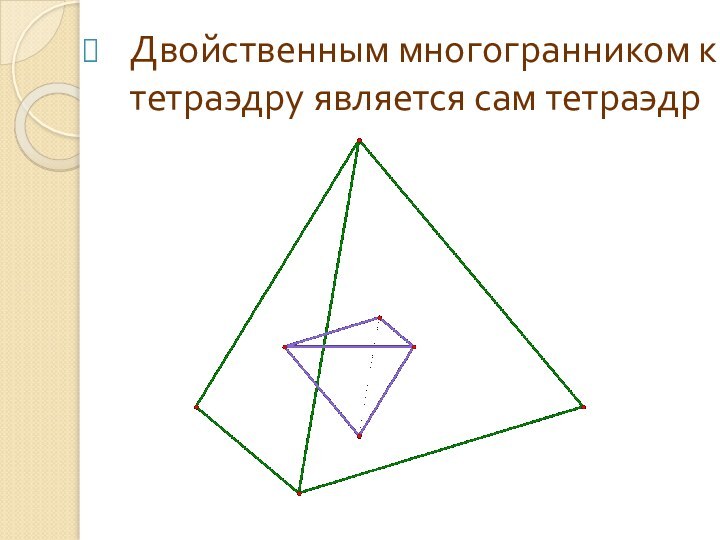
Двойственным многогранником к тетраэдру является сам тетраэдр
Слайд 22
Правильные многогранники – самые выгодные фигуры. И природа
этим широко пользуется.
Многогранники окружают нас в повседневной жизни.
Многогранники в
жизни
Слайд 23
Многогранники в природе
Пчелиные соты – восковые постройки пчёл,
предназначенные для хранения мёда и выращивания потомства.
Они состоят
из правильных многогранников, обращённых внутрь друг к другу под углом 109,28* градусов.
Слайд 24
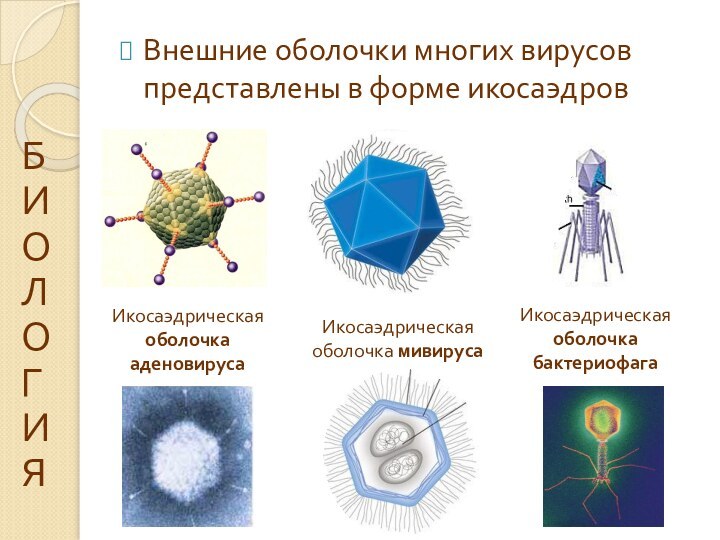
Внешние оболочки многих вирусов представлены в форме икосаэдров
Икосаэдрическая
оболочка аденовируса
Икосаэдрическая оболочка бактериофага
Икосаэдрическая оболочка мивируса
Б
И
О
Л
О
Г
И
Я
Слайд 25
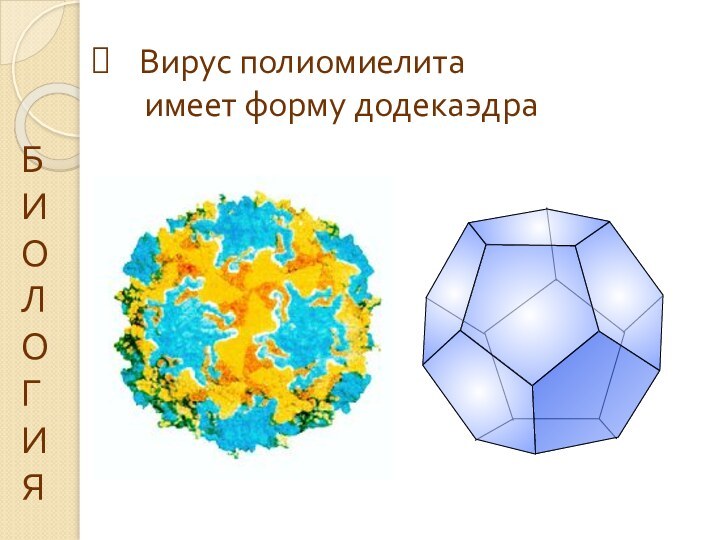
Вирус полиомиелита
имеет форму
додекаэдра
Б
И
О
Л
О
Г
И
Я
Слайд 26
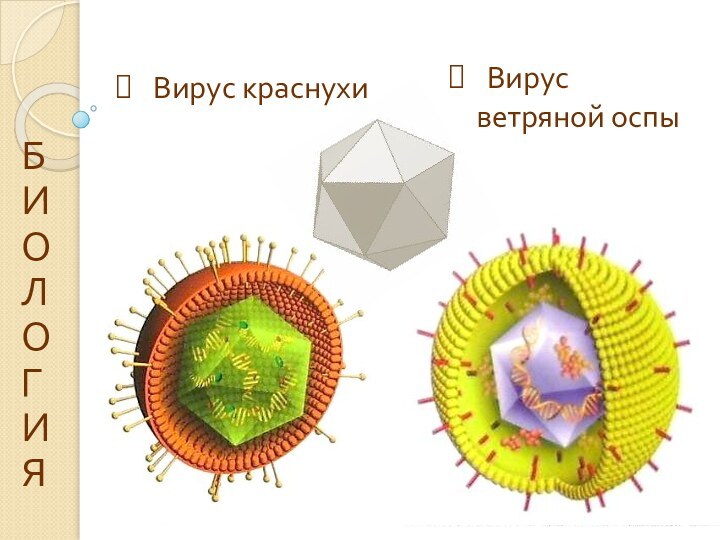
Вирус
ветряной оспы
Вирус краснухи
Б
И
О
Л
О
Г
И
Я
Слайд 27
Скелет одноклеточного организма феодарии по форме напоминает икосаэдр
Б
И
О
Л
О
Г
И
Я
Слайд 28
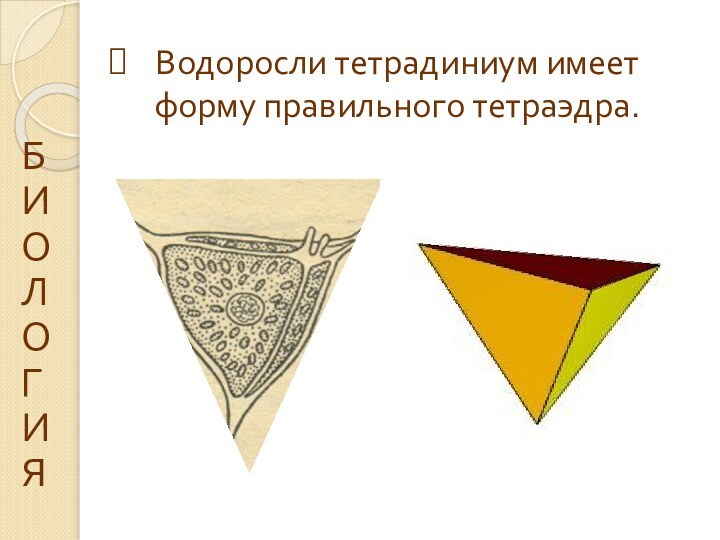
Водоросли тетрадиниум имеет форму правильного тетраэдра.
Б
И
О
Л
О
Г
И
Я
Слайд 29
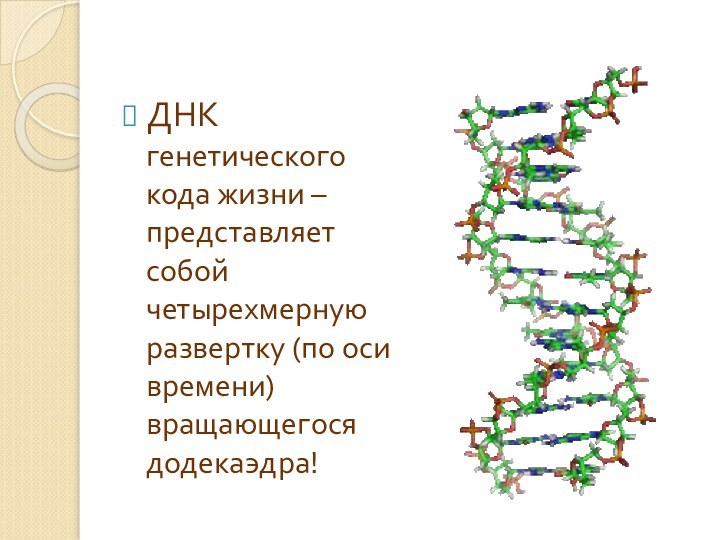
ДНК генетического кода жизни – представляет собой четырехмерную
развертку (по оси времени) вращающегося додекаэдра!
Слайд 30
В естественной среде правильные многогранники можно встретить в
виде кристаллов (минералов).
Форму тетраэдра передает сурьменистый сернокислый натрий.
Х
И
М
ИЯ
Слайд 31
Куб - монокристалл объединяет в себе кристаллы поваренной
соли NaCl.
Х
И
М
ИЯ
Слайд 32
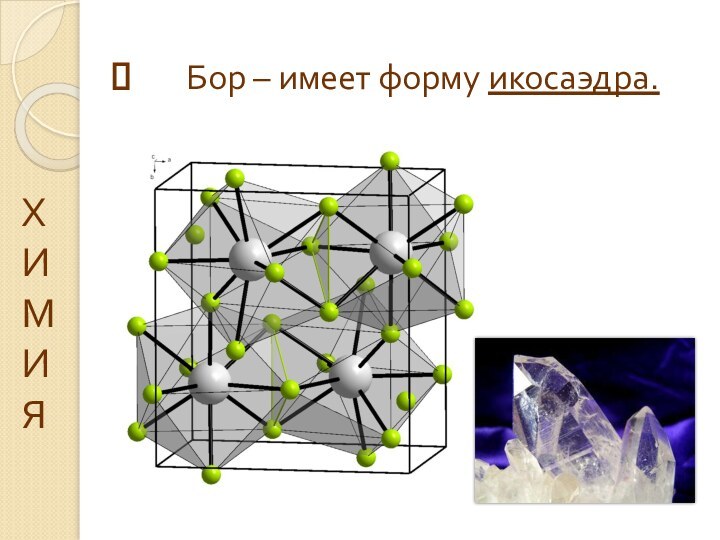
Бор – имеет форму икосаэдра.
Х
И
М
ИЯ
Слайд 33
Х
И
М
ИЯ
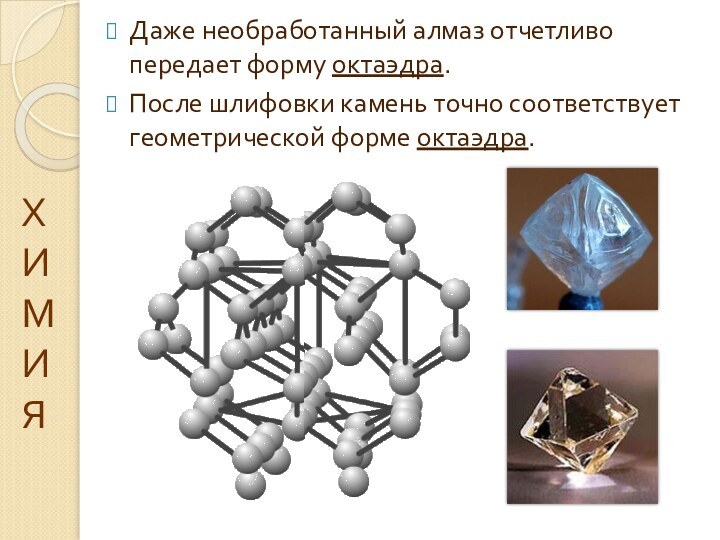
Даже необработанный алмаз отчетливо передает форму октаэдра.
После
шлифовки камень точно соответствует геометрической форме октаэдра.
Слайд 34
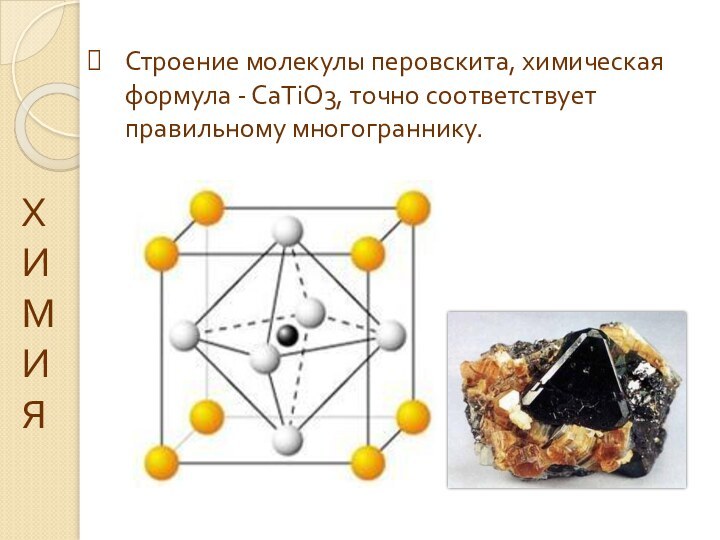
Строение молекулы перовскита, химическая формула - СаТiO3, точно
соответствует правильному многограннику.
Х
И
М
ИЯ
Слайд 35
Кристалл пирита (сернистого колчедана FeS) имеет форму додекаэдра.
Пирит (от греч. “пир” — огонь) — сернистое железо
или серный колчедан, наиболее распространенный минерал из группы сульфидов.
Размеры кристаллов пирита достигают нескольких сантиметров.
Х
И
М
ИЯ
Слайд 36
Многогранники не только объект научных исследований.
Их формы
- завершенные и причудливые, широко используются в декоративном искусстве.
Слайд 37
На картине художника Сальвадора Дали «Тайная Вечеря» Христос
со своими учениками изображён на фоне огромного прозрачного додекаэдра.
Ж
И
ВО
П
И
С
Ь
Слайд 38
Альбрехт Дюрер.
В его известной гравюре «Меланхолия»
на переднем плане
изображен додекаэдр.
Г
Р
А
В
Ю
Р
А
Слайд 39
Ярчайшим примером художественного изображения многогранников в XX веке
являются графические фантазии Маурица Корнилиса Эшера (голландского художника)
Г
Р
А
В
Ю
Р
А
Слайд 40
О
Р
И
Г
А
М
И
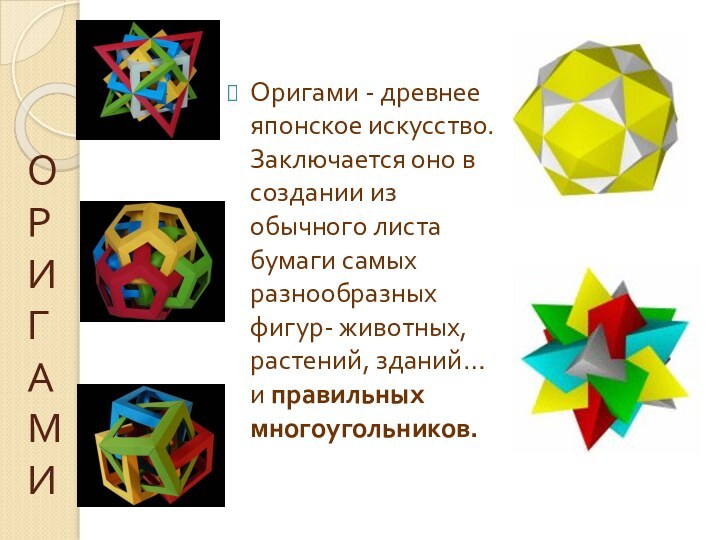
Оригами - древнее японское искусство. Заключается оно в
создании из обычного листа бумаги самых разнообразных фигур- животных,
растений, зданий… и правильных многоугольников.
Слайд 43
г. Мирный (Архангельской обл.) «Большой додекаэдр» - символ
памяти основателям города и космодрома Плесецк.
Памятник додекаэдру в Тонгерене
(Бельгия).
П
А
М
Я
Т
Н
К
И
Слайд 44
П
А
М
Я
Т
Н
К
И
Памятник голове-кубу Ницца (Франция)
г. Ашхабад (Туркменистан)
Слайд 45
Таким образом, оказывается, что вся Вселенная – от
Метагалактики и до живой клетки – построена по одному
принципу– бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции золотого сечения!